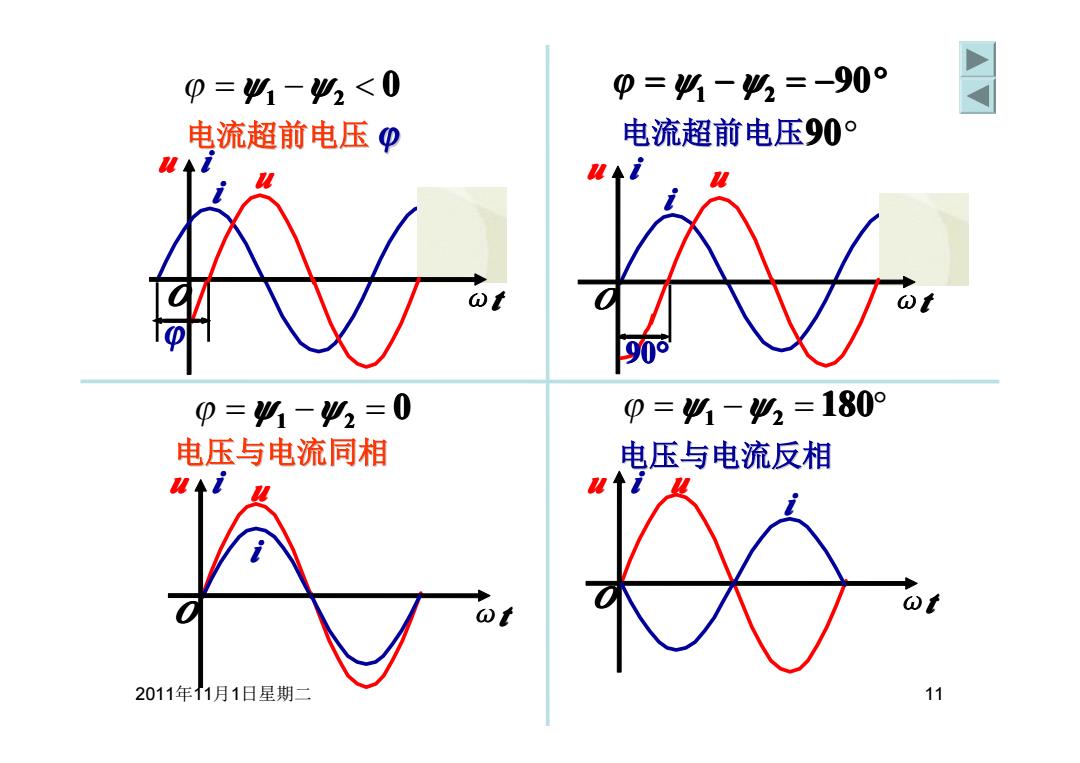
0=91-42<0 0=4-42=-90° 电流超前电压p 电流超前电压0° ◆ u◆d 90° 0=41-42=0 0=4-42=180° 电压与电流同相 电压与电流反相 ◆i 2011年1月1日星期二 11
2011年11月1日星期二 11 电流超前电压 = − = −90° ϕ ψ1 ψ2 90° 电压与电流同相 0 ϕ = ψ1 −ψ2 = 电流超前电压 ϕ 0 ϕ = ψ1 −ψ2 < 电压与电流反相 电压与电流反相 = − = 180° ϕ ψ1 ψ2 u i ωt u i 90° O u i ωt u i O ωt u i u i O u i ωt u i ϕ O
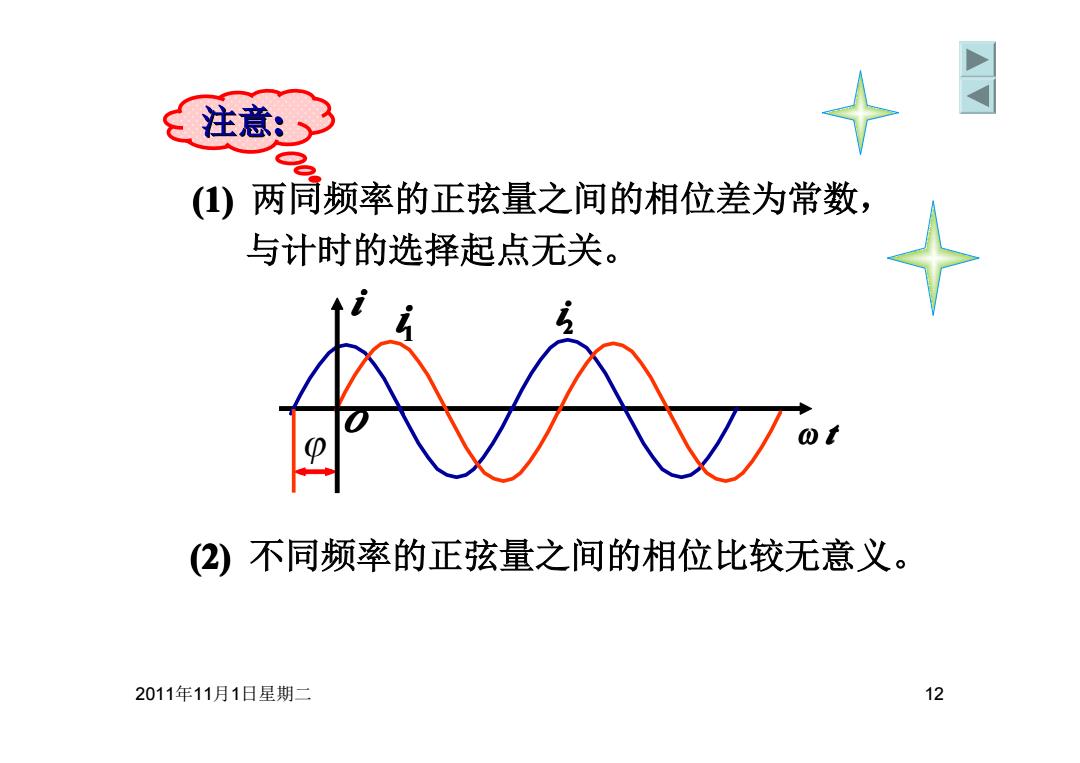
注意: (1)两同频率的正弦量之间的相位差为常数, 与计时的选择起点无关。 2)不同频率的正弦量之间的相位比较无意义。 2011年11月1日星期二 12
2011年11月1日星期二 12 (2) 不同频率的正弦量之间的相位比较无意义。 (1) 两同频率的正弦量之间的相位差为常数, 与计时的选择起点无关。 注意: ω t i 2 i 1 i ϕ O
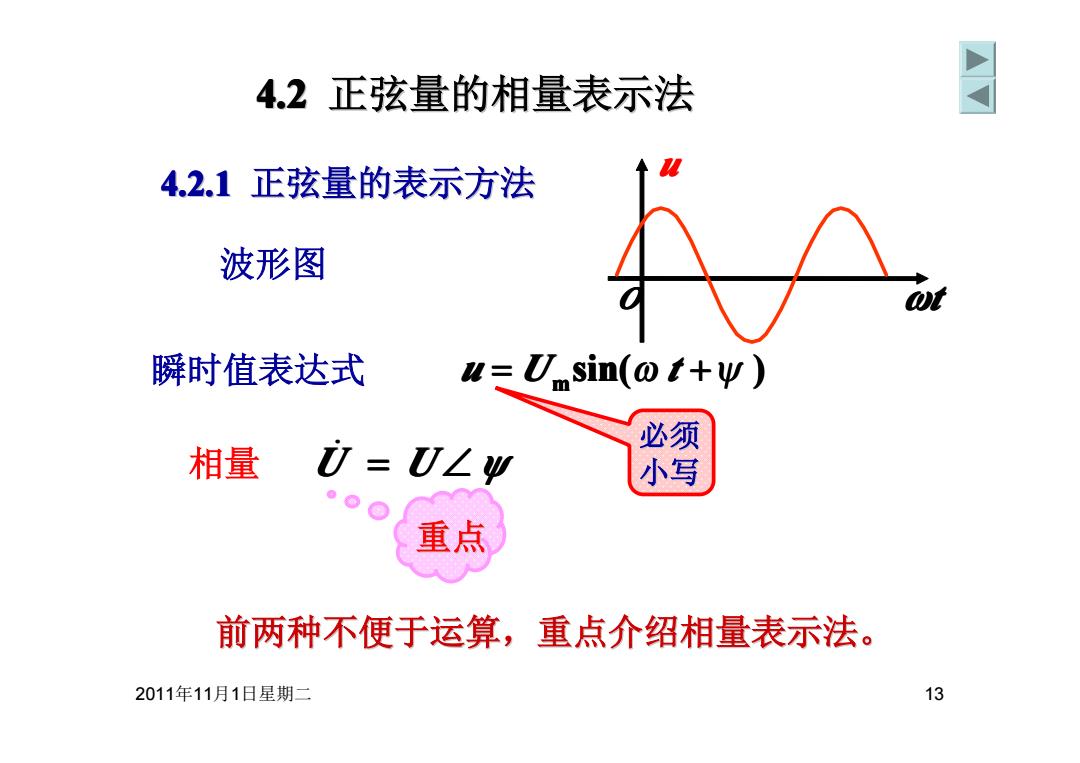
4.2正弦量的相量表示法 4.2.1正弦量的表示方法 波形图 瞬时值表达式 u=U sin(@t+w) 必须 相量 U=U∠ 小写 重点 前两种不便于运算,重点介绍相量表示法。 2011年11月1日星期二 13
2011年11月1日星期二 13 4.2 正弦量的相量表示法 正弦量的相量表示法 瞬时值表达式 sin( ) u = U m ω t +ψ 前两种不便于运算,重点介绍相量表示法。 前两种不便于运算,重点介绍相量表示法。 波形图 4.2.1 正弦量的表示方法 正弦量的表示方法 重点 必须 相量 U = U ∠ ψ 小写 ̇ u O ωt
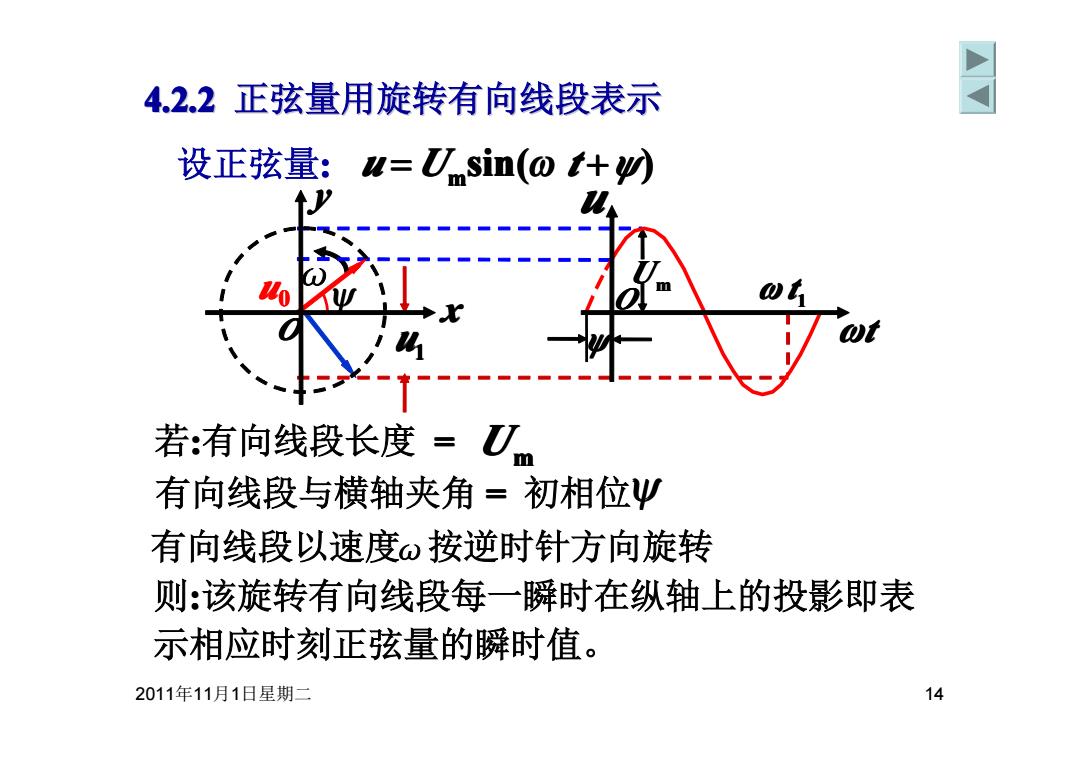
4.2.2正弦量用旋转有向线段表示 设正弦量:u=nsin(ot+) 若:有向线段长度=刀 有向线段与横轴夹角=初相位Ψ 有向线段以速度按逆时针方向旋转 则:该旋转有向线段每一瞬时在纵轴上的投影即表 示相应时刻正弦量的瞬时值。 2011年11月1日星期二 14
2011年11月1日星期二 14 4.2.2 正弦量用旋转有向线段表示 正弦量用旋转有向线段表示 ω sin( ) 设正弦量: u = Um ω t +ψ 若:有向线段长度 = U m 有向线段以速度ω 按逆时针方向旋转 则:该旋转有向线段每一瞬时在纵轴上的投影即表 示相应时刻正弦量的瞬时值。 有向线段与横轴夹角 = 初相位ψ u1 1 u ω t 0 ψ x y O U m ψ u ωt O

4.2.3正弦量的相量表示 实质:用复数表示正弦量 复数表示形式 设为复数: (1)代数式A=a+jb 式中:gr=arctan名 复数的模 复数的辐角 2)三角式 A=cos外jsin(c0sW叶jsinの 由欧拉公式: e”-ejw cOS W= 2 sin= 2j 2011年11月1日星期二 15
2011年11月1日星期二 15 +j +1 b A a r ψ 0 4.2.3 正弦量的相量表示 正弦量的相量表示 复数表示形式 设A为复数: (1) 代数式 A =a + jb a b ψ = arctan 2 2 r = a + b 复数的模 复数的辐角 实质:用复数表示正弦量 实质:用复数表示正弦量 式中: a = r cos ψ b = rsin ψ (2) 三角式 A=rcosψ+jrsinψ=r(cosψ+jsinψ) 由欧拉公式: 2j e e sin j ψ j ψ ψ − − , = 2 e e cos j ψ j ψ ψ − + =