
第四章 随机变量的数字特征 例2(续) §1数学期望 由了的丛问业2 EX=8×0J+∂×03+J0×0Q=∂2 EX=8×0下+∂×02+J0×03=òJ ☑吓·Y本问业下昌·由的斟里水本垂R了的社 合】返回主目录
第四章 随机变量的数字特征 §1 数学期望 解: 例2(续) 甲、乙的平均环数可写为 EX = 80.1+ 90.3+10 0.6 = 9.5 EY =80.2+90.5+100.3= 9.1 因此,从平均环数上看,甲的射击水平要比乙的好. 返回主目录

第四章 随机变量的数字特征 例3 §1数学期望 夺厘『企雪X胳YC9cY业·首最A尿P “+灯 1T司 (0<<+o) 甲1 =十00 -00 深举诅斗丸()业银4·图业E以业基年 +00 合】返回主目录
第四章 随机变量的数字特征 §1 数学期望 设随机变量X 服从Cauchy分布,其密度函数为 由于 ( ) + − x f x dx ( ) (− +) + = x x f x 2 1 1 1 + − + = dx x x 2 1 1 + + = 0 2 1 2 dx x x ( ) + = + 0 2 ln 1 1 x = + 这表明积分 ( ) 不绝对收敛, + − xf x d x 因而EX 不存在. 例3 返回主目录

第四章 随机变量的数字特征 §1数学期望 例4 设离散型随机变量X的分布律为: 1 2 P0.1 0.20.7 则 EX=0*0.1+1*0.2+2*0.7=1.6 若离散型随机变量X的分布律为: X012 P0.70.20.1 则 EX=0*0.7+1*0.2+2*0.1=0.4 此例说明了数学期望更完整地刻化了x的均值状态。 合]返回主目录
设离散型随机变量 X 的分布律为: X 0 1 2 P 0.1 0.2 0.7 例 4 则 EX = 0*0.1+1*0.2+2*0.7 =1.6 若离散型随机变量 X 的分布律为: X 0 1 2 P 0.7 0.2 0.1 则 EX = 0*0.7+1*0.2+2*0.1 =0.4 第四章 随机变量的数字特征 §1 数学期望 此例说明了数学期望更完整地刻化了x的均值状态。 返回主目录
第四章 随机变量的数字特征 例5 按规定,火车站每天800~900,9001000都恰 有一辆客车到站,但到站的时刻是随机的,且两 者到站的时间相互独立,其规律为: 到站时间8:10,9:10 830,930 8:50.9:50 概率 1/6 3/6 2/6 (1)旅客8:00到站,求他侯车时间的数学期望。 (2)旅客820到站,求他侯车时间的数学期望。 解:设旅客的候车时间为X(以分记) (1)X的分布律:X103050 P1/63/62/6 EX=10*(1/6)+30*(376)+50*(2/6)=33.33(分) 合】返回主目录
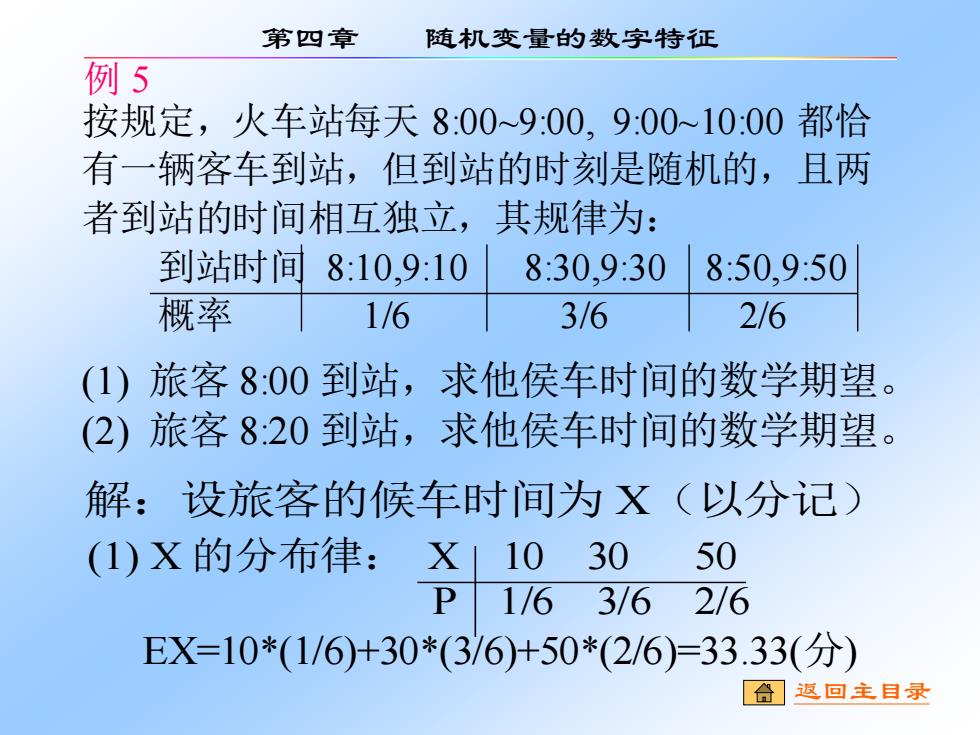
按规定,火车站每天 8:00~9:00, 9:00~10:00 都恰 有一辆客车到站,但到站的时刻是随机的,且两 者到站的时间相互独立,其规律为: 到站时间 8:10,9:10 8:30,9:30 8:50,9:50 概率 1/6 3/6 2/6 例 5 解:设旅客的候车时间为 X(以分记) (1) X 的分布律: X 10 30 50 P 1/6 3/6 2/6 EX=10*(1/6)+30*(3/6)+50*(2/6)=33.33(分) 第四章 随机变量的数字特征 (1) 旅客 8:00 到站,求他侯车时间的数学期望。 (2) 旅客 8:20 到站,求他侯车时间的数学期望。 返回主目录