《电力系统分析》课程教学课件（讲稿）10 电力系统各元件的序阻抗和等值电路

应用叠加原理进行分解 a o ① ①④ (c) ZL ↓ia 27%

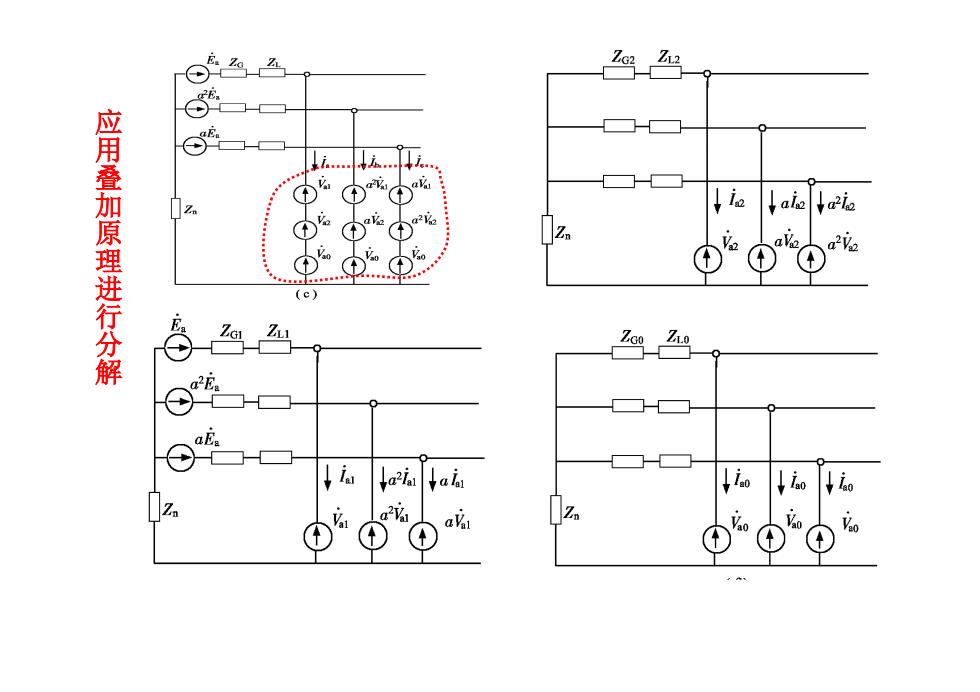
应 用 叠 加 原 理 进 行 分 解

三、对称分量法在不对称短路计算中的应用 >正序网 Ea-ial(ZGl Zu)-(ia +a2ia ala)Zn Val ia +ln +le =ja +a"ia +ala 7=0 E。-ia(ZG1+Zi)='al ↓iaa2iai a27%1 T

三、对称分量法在不对称短路计算中的应用 正序网 1 1 1 2 1 1 1 1 ( ) ( ) a a G L a a a Zn Va E I Z Z I a I aI             1 1 1 1 ( ) a a Z G Z L Va E I       0 1 1 2 1 1 1 1       a a a a b c I I I I I I        

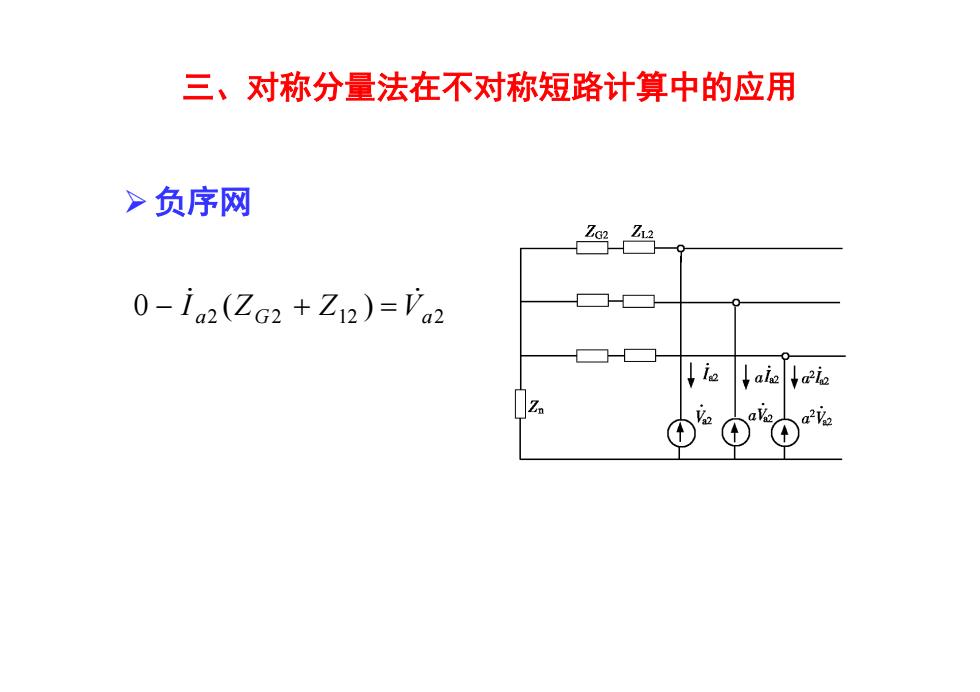
三、对称分量法在不对称短路计算中的应用 >负序网 0-ia2(ZG2+Z12)='a2 ↓ie↓aiaia

三、对称分量法在不对称短路计算中的应用  负序网 2 2 12 2 0 ( ) a Z G Z Va I     

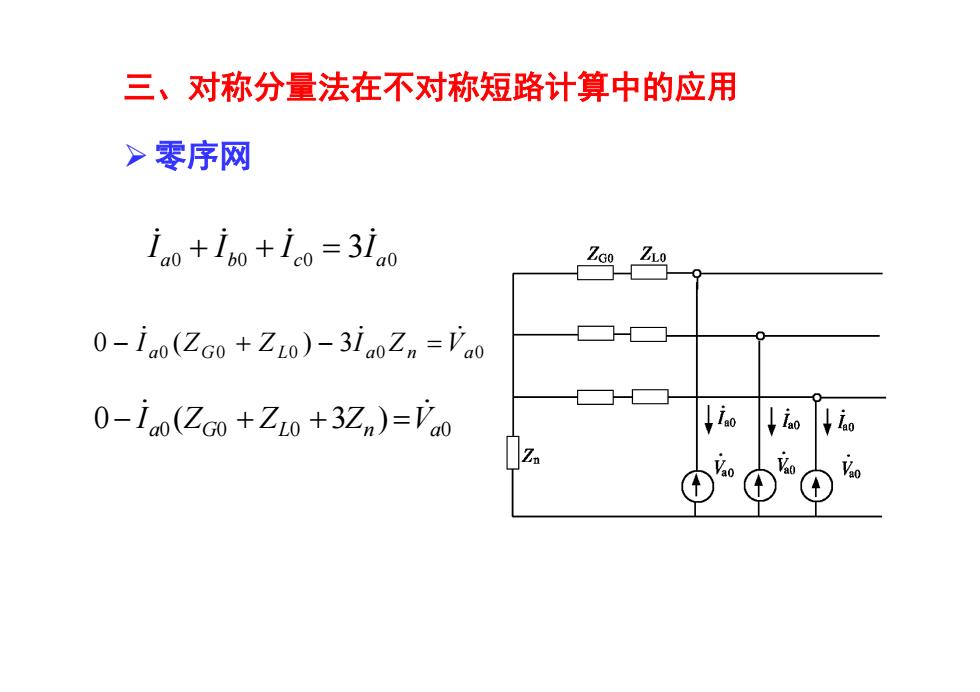
三、对称分量法在不对称短路计算中的应用 >零序网 ioo +Ino+ico=3la0 O-iao(ZGo +ZLo)-3iaoZn Vao O-Iao(ZGo+ZLo+3Zn)=Vao ↓i。↓io

三、对称分量法在不对称短路计算中的应用  零序网 0 0 0 0 0 0 ( ) 3 a G L a Zn Va I Z Z I        0 0 0 0 0 ( 3 ) a ZG ZL Zn Va I       0 0 0 0 3 a b c a I I I I       

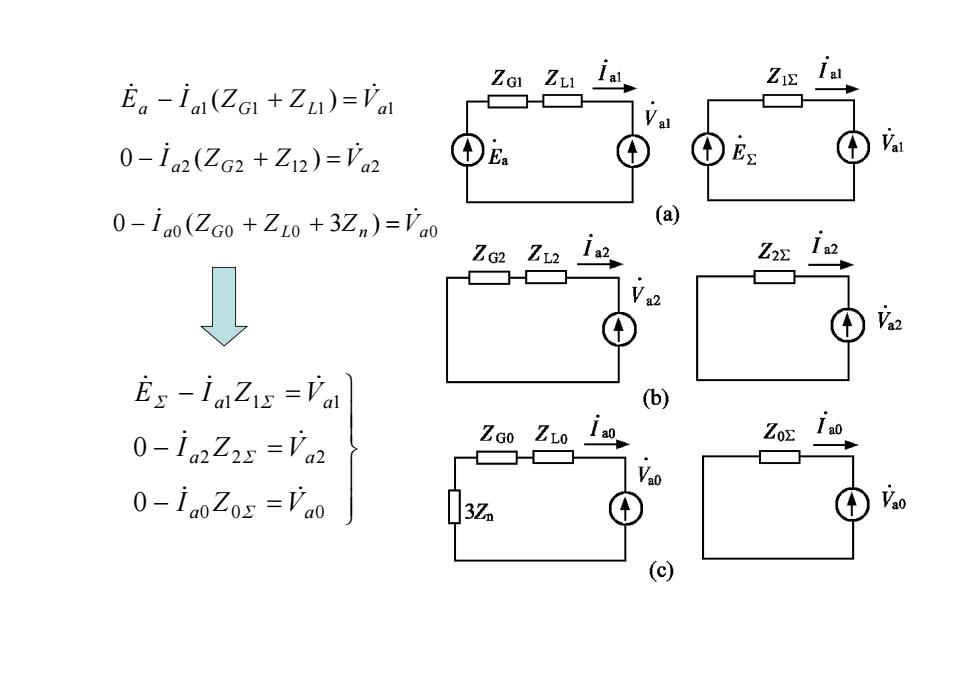
E。-iai(ZG1+Zu)='al 0-i2(ZG2+Z12)='a2 ①Ea ①Ex 0-iao(ZGo +ZLo+3Zn)=Vao (a) ZG2 Z12 1a2 E Es-iaZis=Va (b) a0 0-ig2Z2s =Va2 ZGo ZLo 0-iaoZo=Fao 3Z Vao

1 1 1 1 ( ) a a Z G ZL Va E I       2 2 12 2 0 ( ) a Z G Z Va I      0 0 0 0 0 ( 3 ) a Z G ZL Zn Va I                 0 0 0 2 2 2 1 1 1 0 0 a a a a a a I Z V I Z V E I Z V           