《电力系统分析》课程教学课件（讲稿）10 电力系统各元件的序阻抗和等值电路

二、序阻抗的概念 ·当元件参数完全对称时二a=26b=2cc=2,2b=2c=2ca=二m 「Z-Zm 0 0 Z. 0 0 2z z.+2z0 △'a=Zial 4Y120=ZcI120 AVa2 =Z2ia2 AVao=Zoia0 结论：在三相参数对称的线性电路中，各序对称分量具有独 立性，因此，可以对正序、负序、零序分量分别进行计算

• 当元件参数完全对称时 二、序阻抗的概念 aa bb cc s ab bc ca m z  z  z  z z  z  z  z              0 2 1 0 0 0 0 0 0 0 0 2 0 0 0 0 Z Z Z Z Z Z Z Z Z Z s m s m s m sc 120 120 V Z I   sc           0 0 0 2 2 2 1 1 1 a a a a a a V Z I V Z I V Z I       结论：在三相参数对称的线性电路中，各序对称分量具有独 立性，因此，可以对正序、负序、零序分量分别进行计算

二、序阻抗的概念 ·序阻抗：元件三相参数对称时，元件两端某一序的电压降 与通过该元件的同一序电流的比值。 正序阻抗一Z1=△广ai/ial 负序阻抗一Z2=A广a2/ia2 零序阻抗一Z0=A0/i0

二、序阻抗的概念 • 序阻抗：元件三相参数对称时，元件两端某一序的电压降 与通过该元件的同一序电流的比值。           0 0 0 2 2 2 1 1 1 / / / a a a a a a Z V I Z V I Z V I     正序阻抗   负序阻抗 零序阻抗

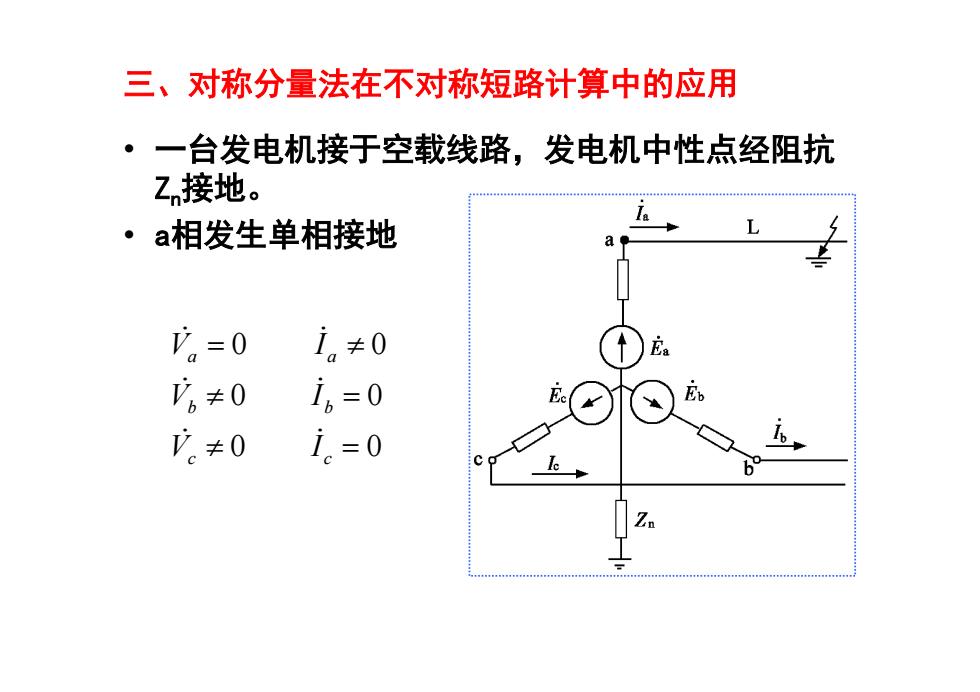
三、对称分量法在不对称短路计算中的应用 ·一台发电机接于空载线路，发电机中性点经阻抗 Zn接地。 ·a相发生单相接地 。=0 i。≠0 。≠0 i。=0 可≠0 i。=0

三、对称分量法在不对称短路计算中的应用 • 一台发电机接于空载线路，发电机中性点经阻抗 Zn接地。 • a相发生单相接地 0 0 0 0 0 0       c c b b a a V I V I V I      

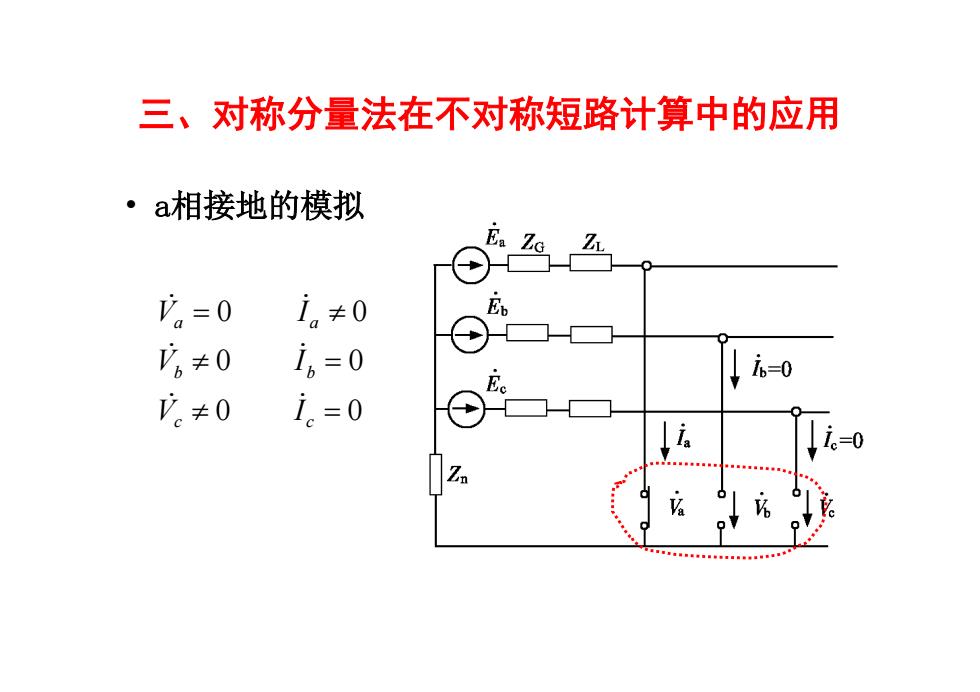
三、对称分量法在不对称短路计算中的应用 ·a相接地的模拟 。=0 in≠0 。≠0 i。=0 ↓-0 。≠0 i。=0

三、对称分量法在不对称短路计算中的应用 • a相接地的模拟 0 0 0 0 0 0       c c b b a a V I V I V I      

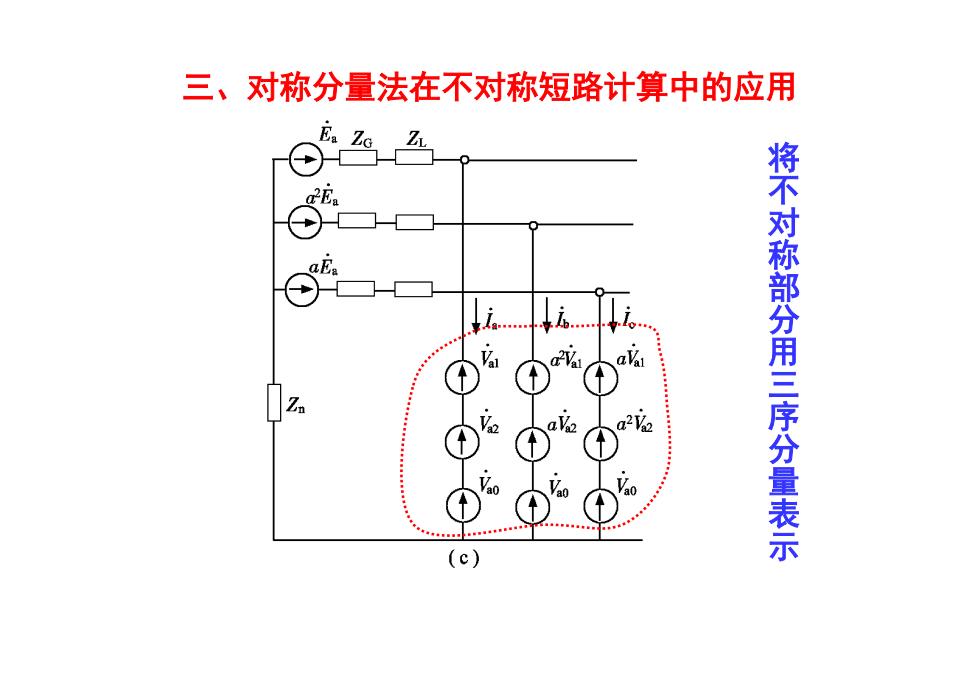
三、对称分量法在不对称短路计算中的应用 Z 2 将不对称部分用三序分量表示 (c)

三、对称分量法在不对称短路计算中的应用 将 不 对 称 部 分 用 三 序 分 量 表 示