河南大学：《电路原理》课程教学资源（课件讲稿）第9章 正弦稳态电路的分析

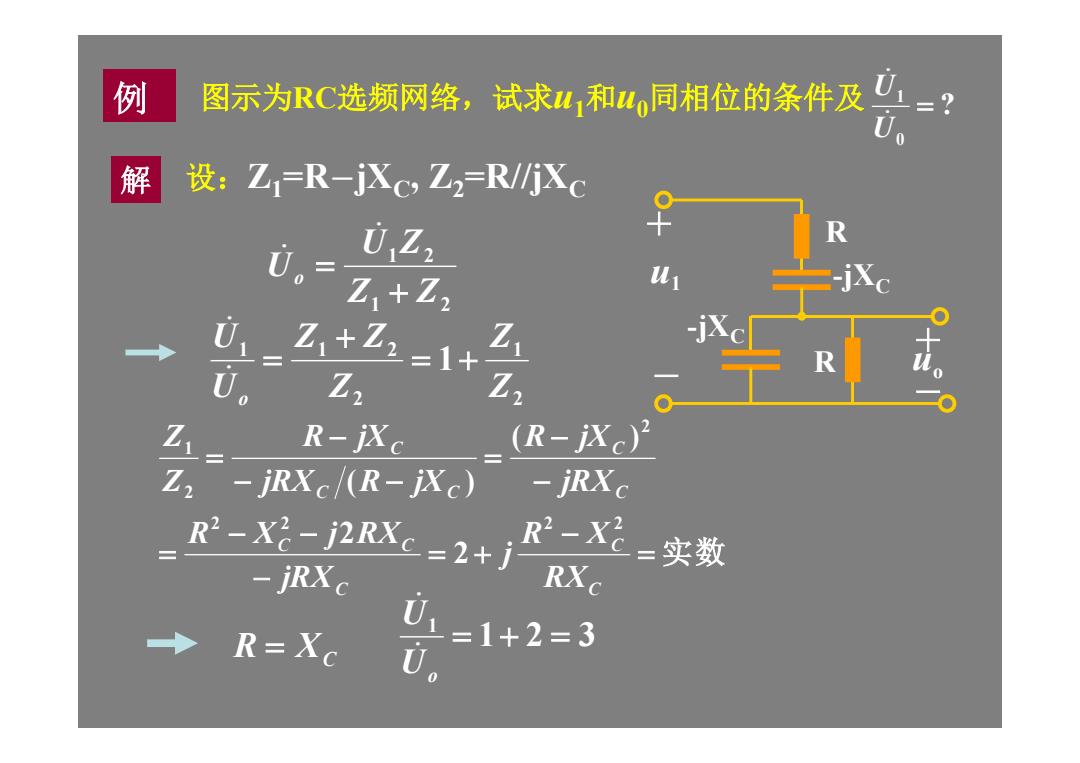
例 图示为RC选频网络， 试求41和同相位的条件及0=？ 解 设：Z1R-jXc,Z2-R/Xc 0+ 0Z2 R Z1+Z2 -jXc Z1+Z2=1+ R R-jXc (-xc)2 Z2-jRXc/(R-jXc)-jRXc R-X-2RXe=2+j R2-X2=实数 -jRXc RX R=Xc 01=1+2=3

例 图示为RC选频网络，试求u1 和u0 同相位的条件及 ? 0 1  U U   -jXC － R － ＋ ＋ R uo u1 -jXC 解 设：Z1=R－jXC , Z2=R//jXC 1 2 1 2 Z Z U Z Uo     2 1 2 1 1 2 1 Z Z Z Z Z U U o        实数               C C C C C C C C C C RX R X j jRX R X j RX jRX R jX jRX R jX R jX Z Z 2 2 2 2 2 2 1 2 2 ( ) ( ) R  XC 1 2 3 1    Uo U  

9.3 正弦稳态电路的分析 电阻电路与正弦电流电路的分析比较： 电阻电路 正弦电路相量分析： KCL: ∑1=0 KCL:∑i=0 KVL: ∑4=0 KVL:∑0=0 元件约束关系：u=R 元件约束关系 :0=Zi 或1=Gu 或i=y0 可见，二者依据的电路定律是相似的。只要作出正弦 电流电路的相量模型，便可将电阻电路的分析方法推广应 用于正弦稳态电路的相量分析中

9. 3 正弦稳态电路的分析 电阻电路与正弦电流电路的分析比较：            i Gu u Ri u i : KVL : 0 KCL: 0 : 或 元件约束关系 电阻电路 : KVL : 0 KCL: 0 :           I Y U U Z I U I       或 元件约束关系 正弦电路相量分析 可见，二者依据的电路定律是相似的。只要作出正弦 电流电路的相量模型，便可将电阻电路的分析方法推广应 用于正弦稳态电路的相量分析中

结论 1.引入相量法，把求正弦稳态电路微分方程的特解 问题转化为求解复数代数方程问题。 2.引入电路的相量模型，不必列写时域微分方程， 而直接列写相量形式的代数方程。 3.:引入阻抗以后，可将所有网络定理和方法都应用 于交流，直流(f=0)是一个特例

结论 1. 引入相量法，把求正弦稳态电路微分方程的特解 问题转化为求解复数代数方程问题。 2. 引入电路的相量模型，不必列写时域微分方程， 而直接列写相量形式的代数方程。 3. 引入阻抗以后，可将所有网络定理和方法都应用 于交流，直流（f =0)是一个特例

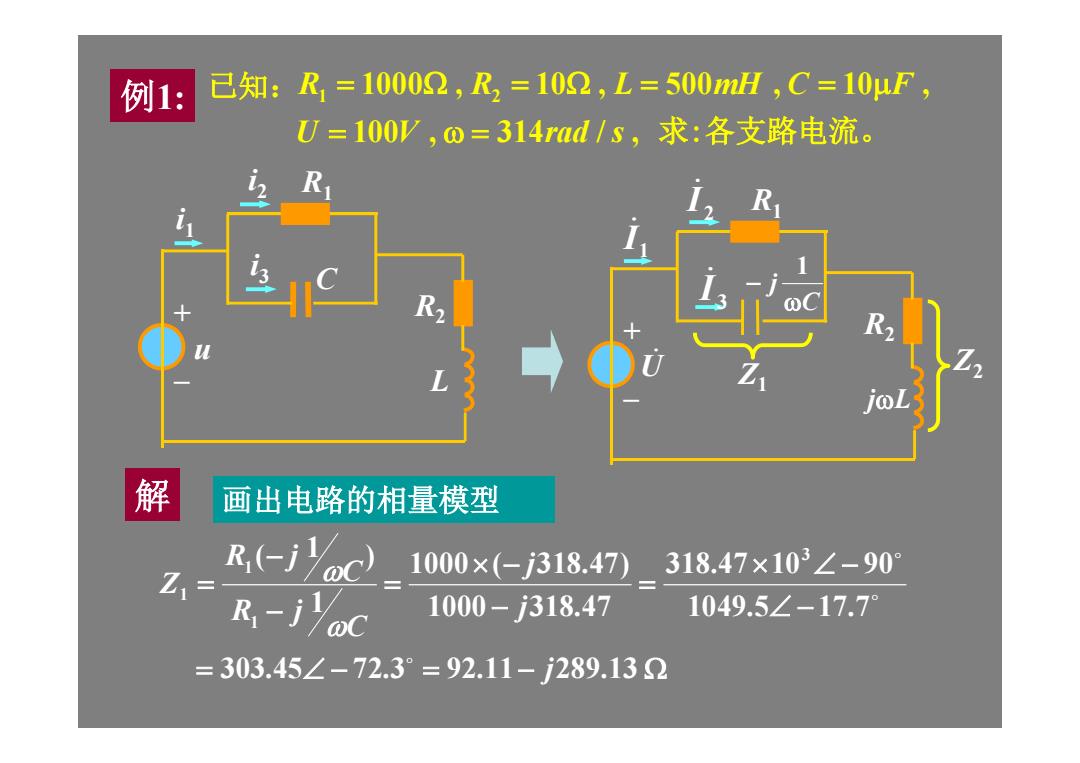
例1： 已知：R=10002,R2=102,L=500mH,C=10μF, U=100V,o=314rad/s，求：各支路电流。 R2 L 解 画出电路的相量模型 R.(-jYoc) 1000×(-j318.47) 318.47×103∠-90 Z1 R,-jYoC 1000-318.47 1049.5∠-17.7° =303.45∠-72.3°=92.11-289.132

例1: + R2 _ L i1 i2 i3 R1 C u Z1 U Z2  + R2 _ R1 1 I  2 I  3 I  C j   1 jL 画出电路的相量模型                    303.45 72.3 92.11 289.13 1049.5 17.7 318.47 10 90 1000 318.47 1000 ( 318.47) 1 ) 1 ( 3 1 1 1 j j j C R j C R j Z      100 , 314 / , 1000 , 10 , 500 , 10 , 1 2 U V rad s R R L mH C F           求:各支路电流。 已知： 解

Z2=R2+j0L=10+j1572 Z=Z+Z =92.11-289.13+10+j157 =102.11-j132.13 =166.99∠-52.3°2 U 100∠0° =0.6∠52.3°A Z 166.99∠-52.3° -j318.47 ×0.6∠52.3°=0.181∠-20°A 1049.5∠-17.7° R 1000 1049.5∠-17.7x0.6∠52.3°=0.57∠70°A R

Z2  R2  jL  10  j157               166.99 52.3 102.11 132.13 92.11 289.13 10 157 1 2 j j j Z Z Z A Z U I      0.6 52.3 166.99 52.3 100 0 1        A j I C R j C j I      0.6 52.3 0.181 20 1049.5 17.7 318.47 1 1 1 1 2               I A C R j R I      0.6 52.3 0.57 70 1049.5 17.7 1000 1 1 1 1 3           Z1 U Z2  + R2 _ R1 1 I  2 I  3 I  C j   1 jL