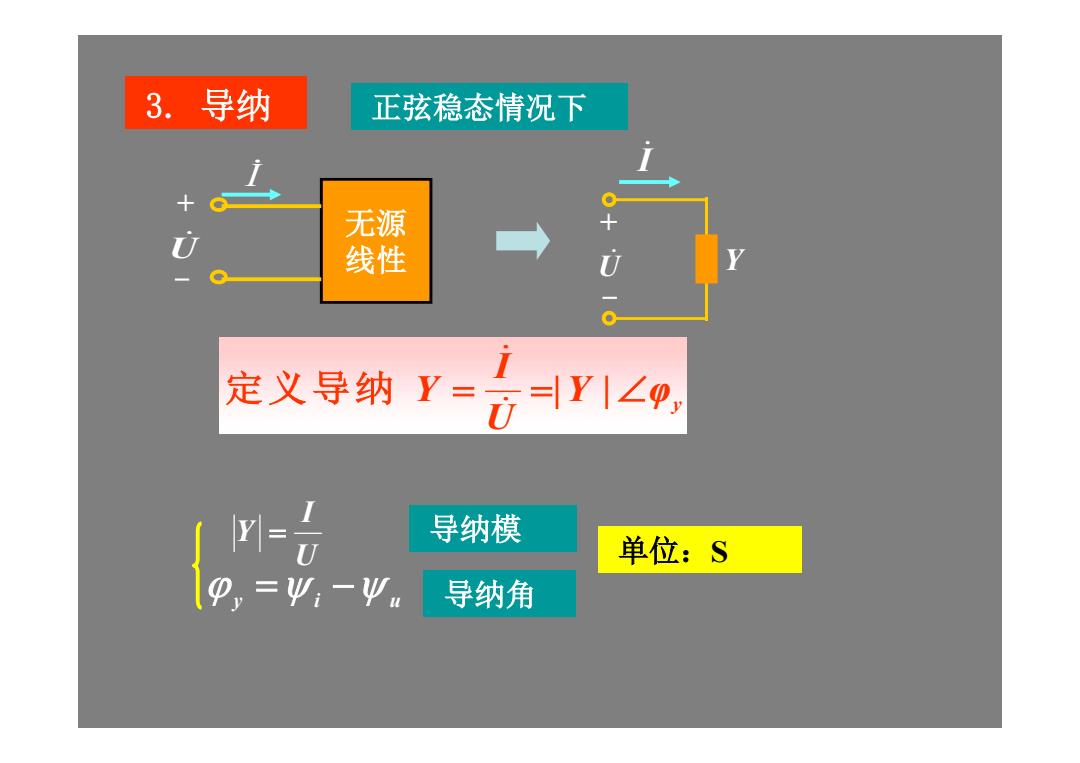
3.导纳 正弦稳态情况下 无源 线性 定义导纳Y= 0=|r1∠p, 导纳模 单位:S 导纳角
3. 导纳 正弦稳态情况下 I U Y + - 无源 线性 I U+ - Y φy U I Y | | 定义导纳 y i u U 单位:S I Y 导纳模 导纳角
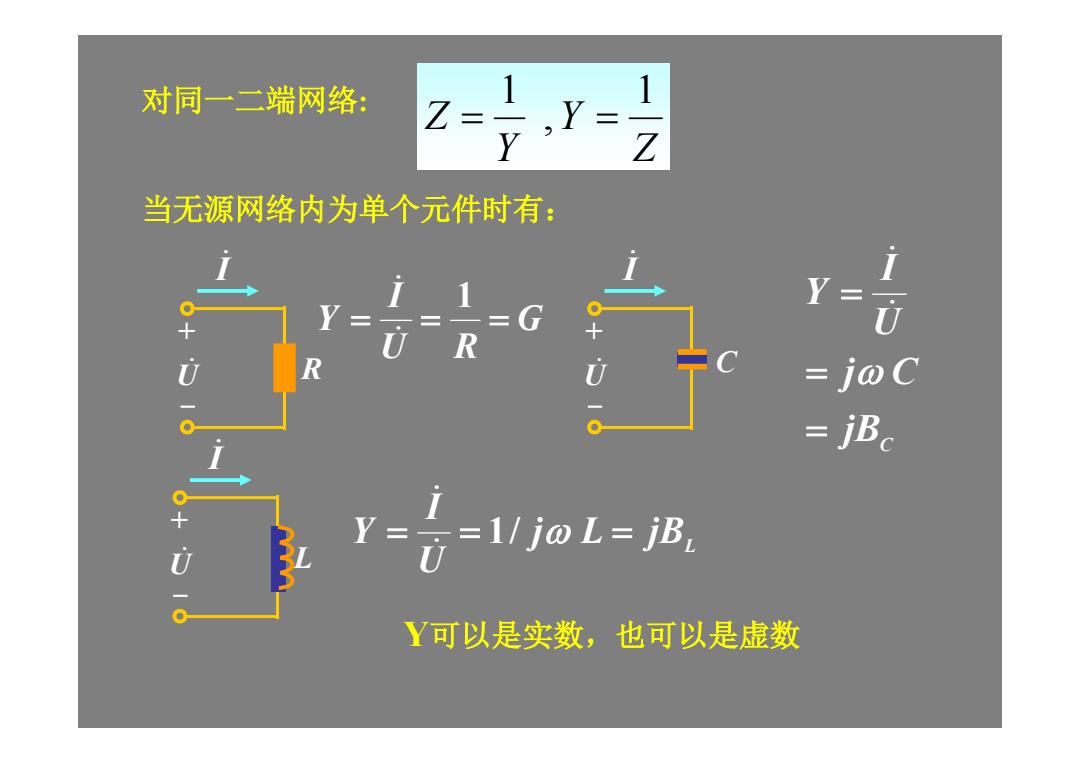
对同一二端网络: 1-Z 当无源网络内为单个元件时有: Y= 而 宁C joC =B。 Y= 7=1/j0L=B Y可以是实数,也可以是虚数
Z Y Y Z 1 , 1 对同一二端网络: 当无源网络内为单个元件时有: G U R I Y 1 L j L jB U I Y 1/ C jB j C U I Y I U R + - I C U+ - I U L + - Y可以是实数,也可以是虚数
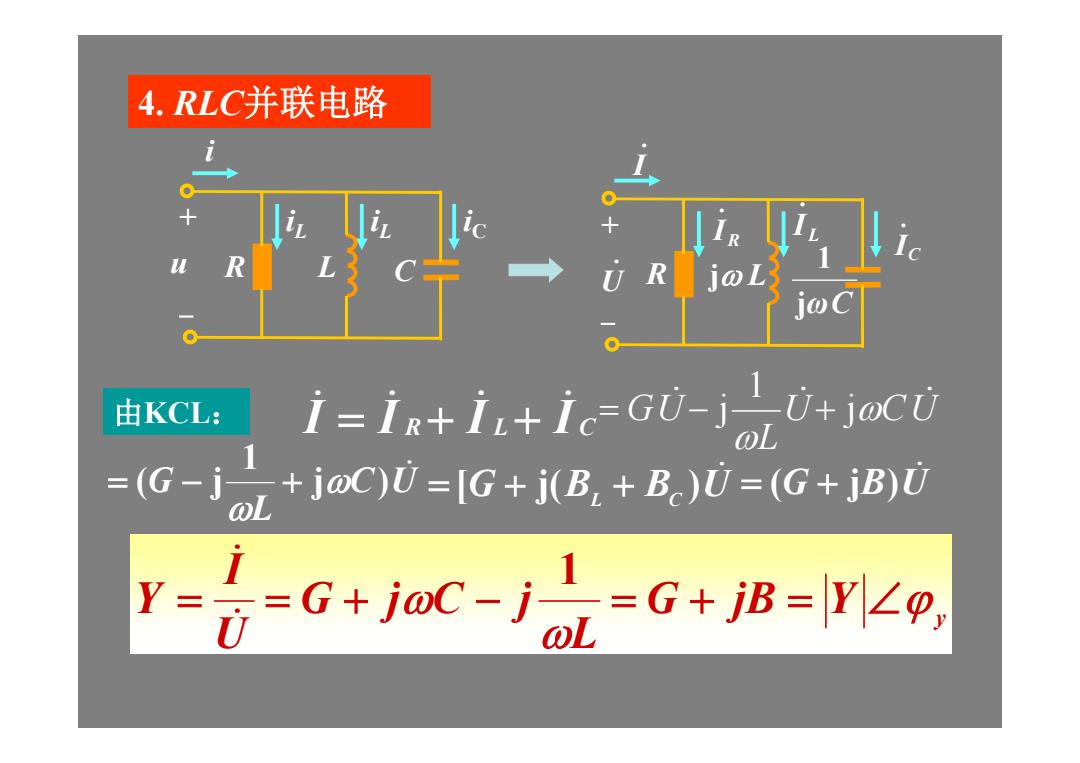
4.RLC并联电路 jωC 由KCL: i=ix+i.+ic=GU-j-U+jocU ol (G-j1+joC)0=G+j(B,+B)0=(G+jB)0 Y= G-G+Joc-J ot=G
4. RLC并联电路 由KCL: I I R I L I C i u R L C iL iC + - iL j 1 j U CU L GU j ) 1 ( j C U L G [G j(BL BC )U (G jB)U .I j L . U I L . IC . jωC 1 IR . R + - Y y G jB L G j C j U I Y 1

Y一复导纳;G一电导(导纳的实部);B一电纳(导纳的虚部): 一复导纳的模;P,一导纳角。 转换关系:1|Y=VG2+B2 B 9,arct G 或 C 导纳三角形 Y B G
Y— 复导纳;G—电导(导纳的实部);B—电纳(导纳的虚部); |Y|—复导纳的模; y—导纳角。 转换关系: arctg | | 2 2 G B φ Y G B y 或 G=|Y|cos y B=|Y|sin y 导纳三角形 |Y| G B y y i u U I Y
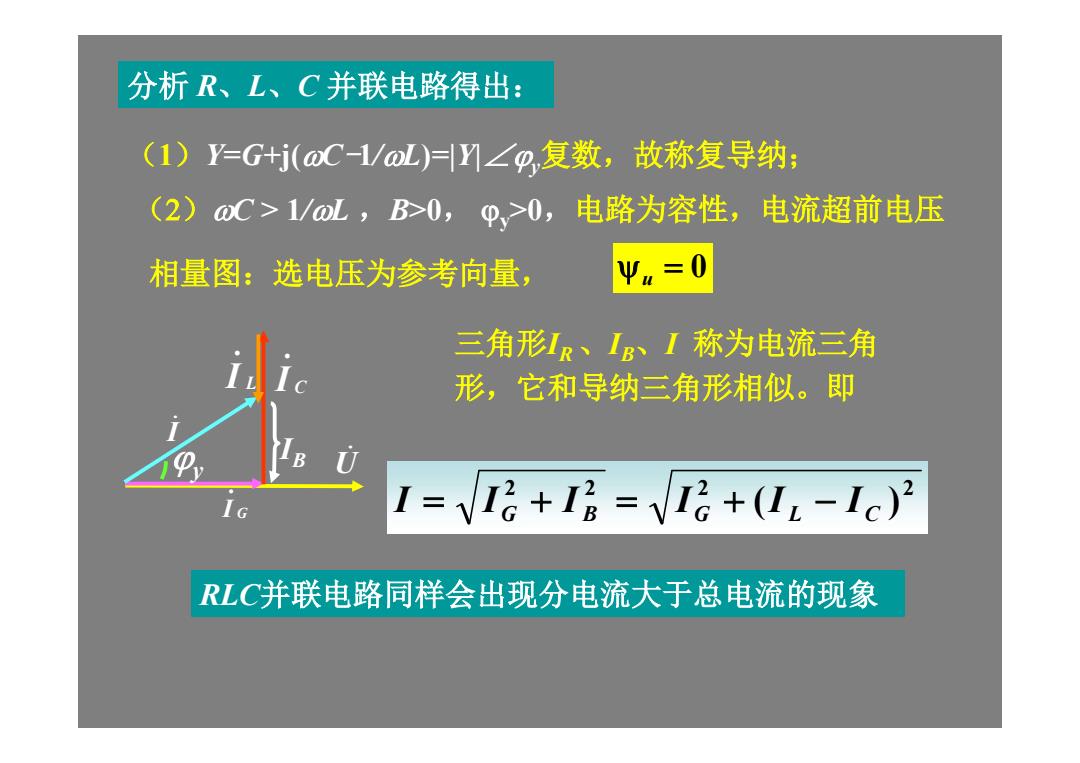
分析R、L、C并联电路得出: (1)Y=G+j(oC-1/oL)=I∠g复数,故称复导纳: (2)oC>1/oL,B>0,p,>0,电路为容性, 电流超前电压 相量图:选电压为参考向量, y=0 三角形IR、IB、I称为电流三角 形,它和导纳三角形相似。即 I=Ig+I=Ig+(I1-Ic)2 RLC并联电路同样会出现分电流大于总电流的现象
(1)Y=G+j(C-1/L)=|Y|∠y 复数,故称复导纳; (2)C > 1/L ,B>0, y>0,电路为容性,电流超前电压 相量图:选电压为参考向量, 2 2 2 2 ( ) G B G L C I I I I I I U I G . I C . I y I L . u 0 分析 R、L、C 并联电路得出: 三角形IR 、IB 、I 称为电流三角 形,它和导纳三角形相似。即 RLC并联电路同样会出现分电流大于总电流的现象 IB