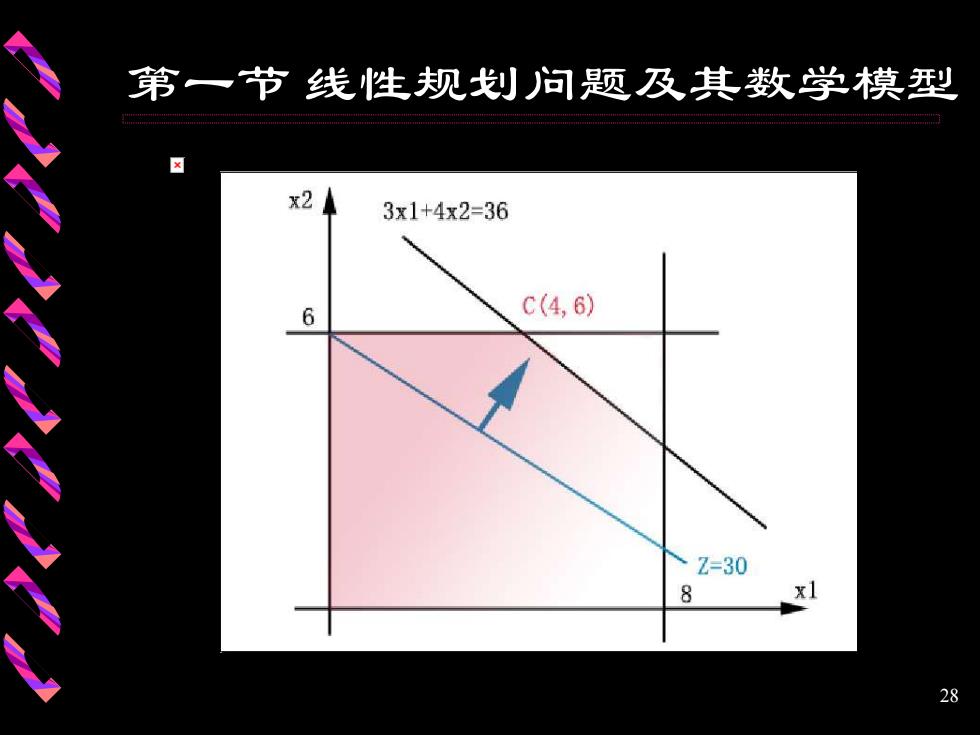
第一节线性规划问题及其数学模型 x2 3x1+4x2=36 6 C(4,6) Z=30 8 x1 28
28 第一节 线性规划问题及其数学模型

第二节线性规划的解及其性质 线性规划解的概念 (1)可行解 满足LP问题所有约束条件的向量X称为可行 解,所有可行解构成的集合称为可行域,记为R。 譬如标准形LP问题的可行解为满足(1-4)的向 量X=(x1”x2,X)T,其可行域为: R={X|AX=b,X≥0,b≥0}。 般来说,可行解有无限多个。 29
29 第二节 线性规划的解及其性质 一、线性规划解的概念 (1)可行解 满足LP问题所有约束条件的向量X称为可行 解,所有可行解构成的集合称为可行域,记为R。 譬如标准形LP问题的可行解为满足(1-4)的向 量X = ( x1,x2,.,xn ) T ,其可行域为: R= { X | AX = b,X≥0,b≥0 }。 一般来说,可行解有无限多个

第二节线性规划的解及其性质 (2)最优解 满足目标要求的可行解称之为最优解,记为 X*,它所对应的目标函数值称为最优值,记为Z*。 有时把X,Z*统称为最优解 。 譬如标准形LP问题的最优解是满(1-4),同时 使目标函数Z=CX达到最大值的解向量为: X*=(X1*,X2*, 最优值为Z*=CTX 30
30 第二节 线性规划的解及其性质 (2)最优解 满足目标要求的可行解称之为最优解,记为 X* ,它所对应的目标函数值称为最优值,记为Z* 。 有时把X* ,Z*统称为最优解。 譬如标准形LP问题的最优解是满(1-4),同时 使目标函数Z=CTX达到最大值的解向量为: X* = ( x1 * ,x2 * ,.,xn * ) T , 最优值为Z* = C TX*

第二节线性规划的解及其性质 (3)基与基解 基的概念只适用于LP问题的标准形。在引出 这一概念之前,先就范例的标准形进行研讨。 maxZ=3x1+5x2+0x3+0x4+0x5 1x1+0x2+1x3+0x4+0x5=8 0x1+2x2+0x3+1x4+0x5=12 (1-5) 3x1+4x2+0x3+0x4+1x5=36 X1,X2?x3yX4?x5≥0 31
31 第二节 线性规划的解及其性质 (3)基与基解 基的概念只适用于LP问题的标准形。在引出 这一概念之前,先就范例的标准形进行研讨。 max Z = 3x1+ 5x2+ 0x3+0x4+ 0x5 + + + + = + + + + = + + + + = 0 3 4 0 0 1 36 0 2 0 1 0 12 1 0 1 0 0 8 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 x x x x x x x x x x x x x x x x x x x x , , , , (1-5)
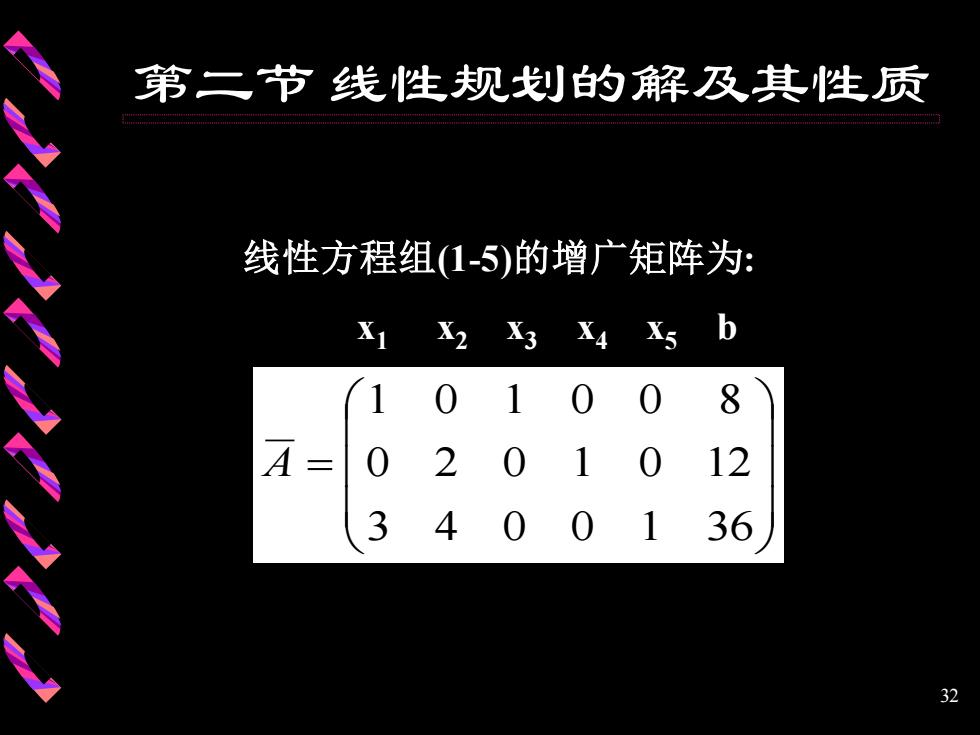
第二节线性规划的解及其性质 线性方程组(1-5)的增广矩阵为: X1 X2 X3 X4 X5 b 8 A = 0 2 1 12 3 4 36 32
32 第二节 线性规划的解及其性质 线性方程组(1-5)的增广矩阵为: x1 x2 x3 x4 x5 b = 3 4 0 0 1 36 0 2 0 1 0 12 1 0 1 0 0 8 A