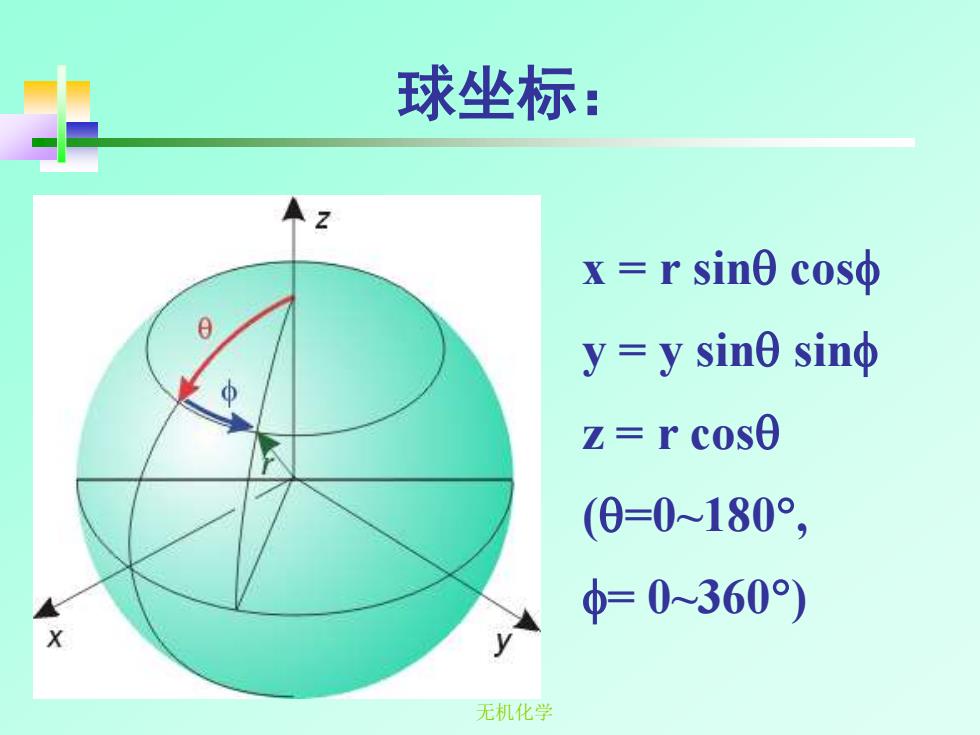
球坐标: x=rsin0cosφ y =y sine sino z=r cos0 (0=0~180°, φ=0-360) 无机化学
无机化学 球坐标: x = r sin cos y = y sin sin z = r cos (=0~180 , = 0~360)

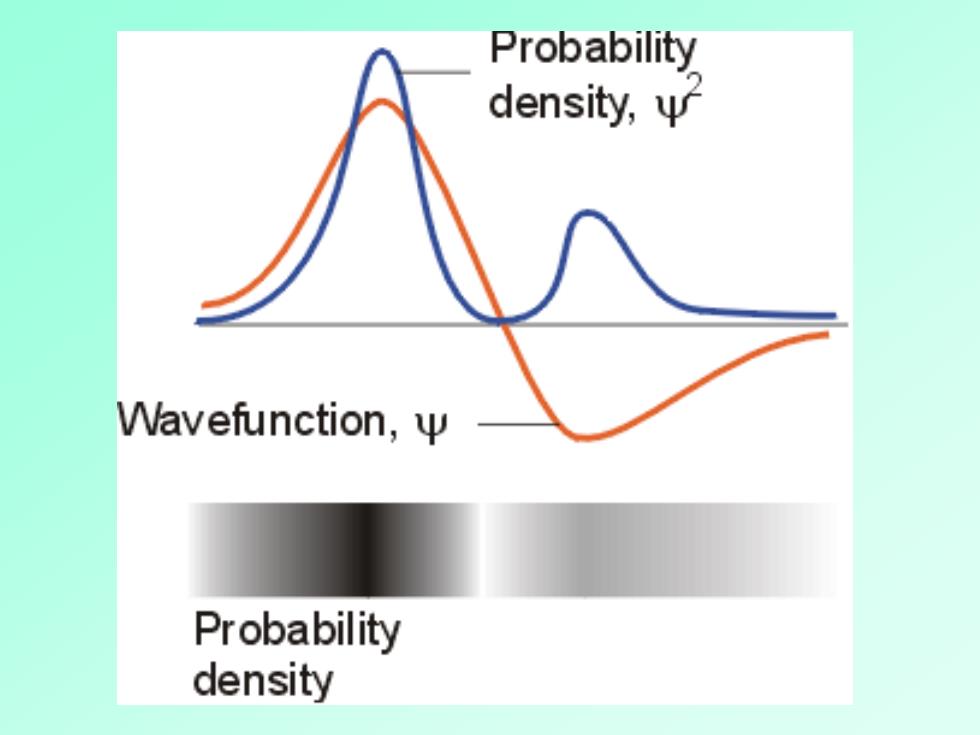
几率密度(y2) 几率密度(Ψ川2):电子在原子空间上某点附近 单位微体积内出现的几率。 IΨ2的物理意义:(1926年,德国,Borm) Ψ2值大,表明单位体积内电子出现的几率大, 即电荷密度大;Ψ2值小,表明单位体积内电 子出现的几率小,即电荷密度小。 电子在空间的几率分布,即Ψ2在空间的 分布称“电子云”。 无机化学
无机化学 几率密度(|| 2) 几率密度(|| 2):电子在原子空间上某点附近 单位微体积内出现的几率。 | | 2的物理意义: (1926年,德国, Born) | | 2 值大,表明单位体积内电子出现的几率大, 即电荷密度大;| | 2 值小,表明单位体积内电 子出现的几率小,即电荷密度小。 电子在空间的几率分布,即| | 2 在空间的 分布称“电子云
Probability density,y Wavefunction,y Probability density

波函数以及常数n,/,m 电子的运动状态可由Schr6 dinger方程解得的波函 数y来描述。为得到合理解,在解Schrodinger方 程中,波函数中引入了常数项n、1、m、m,其 意义见后,取值范围为: n=1,2,3,.0 l=0,1,2,.n-1 m=0,±1,±2,.±l m,=±1/2 每种波函数对应于电子的一种运动状态。通常把 一种波函数称为一个原子轨道。但这里的轨道, 不是经典力学意义上的轨道,而是服从统计规律 的量子力学意义上的轨道。 无机化学
无机化学 波函数以及常数 n、 l、m 电子的运动状态可由Schrődinger方程解得的波函 数来描述。为得到合理解,在解Schrődinger方 程中,波函数中引入了常数项 n、 l、m、ms,其 意义见后,取值范围为: n = 1, 2, 3, . l = 0, 1, 2, .n-1 m = 0, 1, 2, . l ms = 1/2 每种波函数对应于电子的一种运动状态。通常把 一种波函数称为一个原子轨道。但这里的轨道, 不是经典力学意义上的轨道,而是服从统计规律 的量子力学意义上的轨道

3、四个量子数 Name Symbol Values Meaning Indicates 名称 符号 取值 表示 指明 principle n 1,2, shell,电子层 size 主量子数 energy能层 尺寸 Orbital 0,1 subshell shape angular 1 energy 形状 momentum 亚层能级 角量子数 magnetic m 0,±1,±2, orbitals of direction 磁量子数 .y±/ subshelli亚层 方向 轨道 Spin magnetic ms +1/2,- spin state Spin 自旋磁量子数 1/2 自旋状态 direction 自旋方向
无机化学 3、四个量子数 Name 名称 Symbol 符号 Values 取值 Meaning 表示 Indicates 指明 principle 主量子数 n 1, 2, shell, 电子层 energy 能层 size 尺寸 Orbital angular momentum 角量子数 l 0, 1,, n- 1 subshell energy 亚层能级 shape 形状 magnetic 磁量子数 m 0, 1, 2, , l orbitals of subshell亚层 轨道 direction 方向 Spin magnetic 自旋磁量子数 ms + 1 / 2 , - 1/2 spin state 自旋状态 Spin direction 自旋方向