[n]一个周期的DTT: ee Ex.8.6 IX(ej)1,Ik]l magnitude 0= sampling 3元 4π 0 8 20 X[-et4aMo)sinπk/2 phase 文X(ei),文X[k] sin(πk/10) 4 20 k
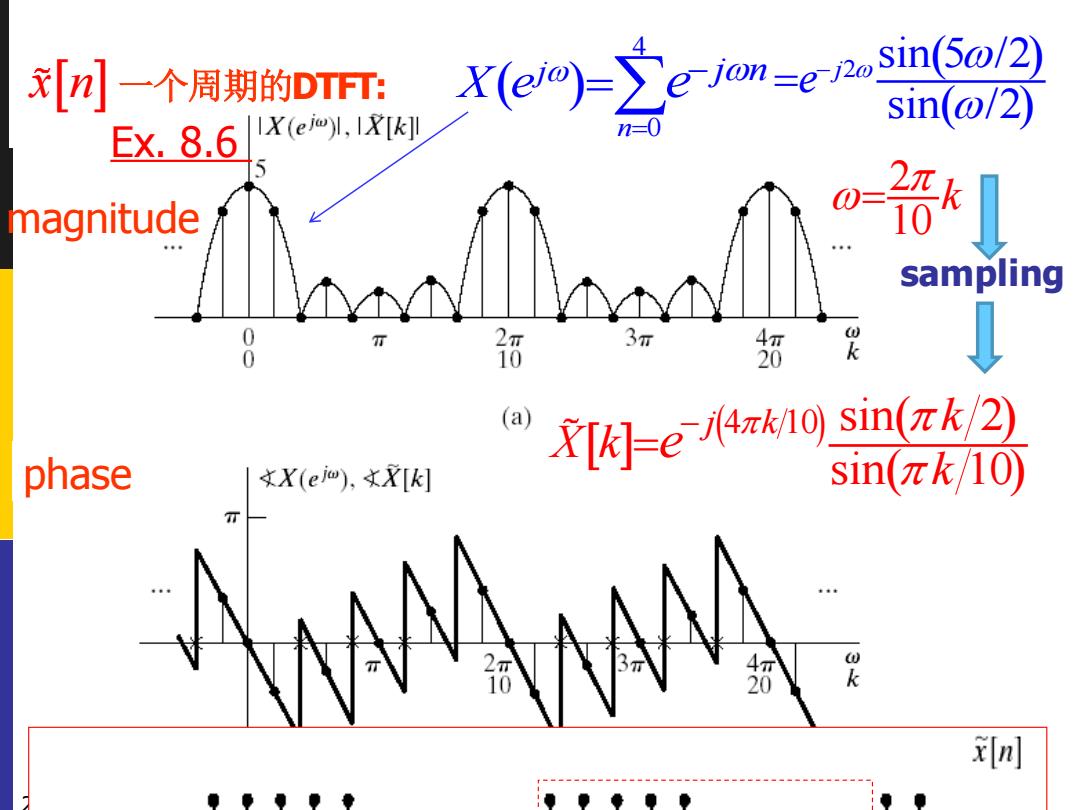
magnitude of the DFS 21 ( ) ( ) ( ) 4 10 sin 2 sin 10 j k k X k k e − = magnitude phase ( ) 4 n 0 j j n X e e = − = ( ) ( ) 2 sin 5 /2 sin /2 j e − = sampling x n 一个周期的DTFT: Ex. 8.6 2 10 k =

8.2 Properties of the Discrete Fourier Series ◆8.2.1 Linearity For two periodic sequence,both with period N,such that: DFS [刊←>[k],《→[k] then DFS a [n]+b[n<axi[k]+bx2[] 7
22 8.2 Properties of the Discrete Fourier Series ◆8.2.1 Linearity ◆For two periodic sequence, both with period N, such that: 1 1 , DFS x n X k x n X k DFS 2 2 ~ ~ 1 2 1 2 DFS ax n bx n aX k bX k + + then

8.2 Properties of the Discrete Fourier Series 8.2.2 Shift of a sequence DFS ◆if [n]←→[k] DFS then n-m←>W"X[k],W侬m=e2πMm DFS and Wymlnx[k-l],wml-ereriNyl shift in the Fourier coefficients by an integer / 72
23 8.2 Properties of the Discrete Fourier Series ◆8.2.2 Shift of a sequence DFS x n X k DFS N km x n X k −m W , DFS N nl W l x n X k − − , j N km (2 ) N W e km − = j N (2 ) N W e −nl nl = ◆if then and shift in the Fourier coefficients by an integer l

8.2 Properties of the Discrete Fourier Series ◆8.2.3 Duality DFS DFS [n←→[k] →[n]←>N[-k] 刘川 1, [n川 n 01 2 …N-1 012.N-1 [k] N [-K] k 012·N-1 0 12…N-1 24 Example 8.2
24 8.2 Properties of the Discrete Fourier Series ◆8.2.3 Duality DFS x n X k DFS X n Nx k− 0 1 2 …… N-1 X n n 1 1 X k 0 1 2 …… N-1 k x n 0 1 2 …… N-1 n 1 0 1 2 …… N-1 Nx k − k N Example 8.2

8.2 Properties of the Discrete Fourier Series ◆8.2.3 Duality DFS DFS [n]←>[k] →[n]→[-k] Proof: n][n]PFS coefficients [k]=∑nw according Y[k]=[n]w n=0 defination n=0 V- interchang the roles of n and k [-k]=∑[n]w n=0 网=∑[例w NXn time inverse →[-n川]=∑[W defination 8.2.4 Symmetry Properties 25
25 8.2 Properties of the Discrete Fourier Series ◆8.2.3 Duality DFS x n X k DFS X n Nx k− ◆8.2.4 Symmetry Properties 1 0 1 N kn N k x n X k W N − − = = 1 0 N kn N n X k x n W − = = Proof: 1 0 N N kn k Nx X W n k − = − = 1 0 kn n N Y X WN k n − = = interchang the roles of n and k according defination 1 0 N N kn n Nx X W k n − = − = yn = X n defination N× time inverse DFS coefficients x n