
Ex.8.1 DFS of a impulse train N points 河 -N-N+1…·-2-101 2 N-1NN+1N+2 之--收m N points [k] k -N-N+1…·-2 -1 0 1 ·N-1N N+1N+2 N- 2π [k]=∑δ[nW"=W8=l, =e - n=0 网天Σ]= 21 kn 入 orthogonality
15 Ex. 8.1 DFS of a impulse train 1 0 0 1, N kn N N n X k n W W − = = = = 0 1 -N -N+1…… -2 -1 2 …… N-1 N N+1 N+2 …… N points X k ~ k 1 1 0 1 N kn N k x n X k W N − − = = 1, , 0, n rN r is any integer otherwise = = r x n n rN =− = − 0 1 -N -N+1…… -2 -1 2 …… N-1 N N+1 N+2 …… N points xn 1 ~ 0 1 2 1 N j k N n k e N − = = 2 N j W N e − = orthogonality

Example 8.2 Duality in the Discrete Fourier Series If the Discrete Fourier Series coefficients is the periodic impulse train,determine the signal. N points []=∑Nδ[k-rN] N [内 -N ·-2-1012…N-1N ...k Solution: 2w-艺6[-时-1 k=0 k=0 =∑[w“DS[]-∑[]w n=0
16 Example 8.2 Duality in the Discrete Fourier Series ◆If the Discrete Fourier Series coefficients is the periodic impulse train, determine the signal. r Y k k rN N =− = − 1 0 1 kn N N k y Y k W N n − − = = 1 0 1 N kn N k x n X k W N − − = = 0 1 2 … … N … -2 -1 … … -N … N points N Y k N N N-1 k Solution: DFS 0 1 0 1 1 k N k n N N k W N N W − = − = = = 1 0 N kn N n X k x n W − = = y n N points
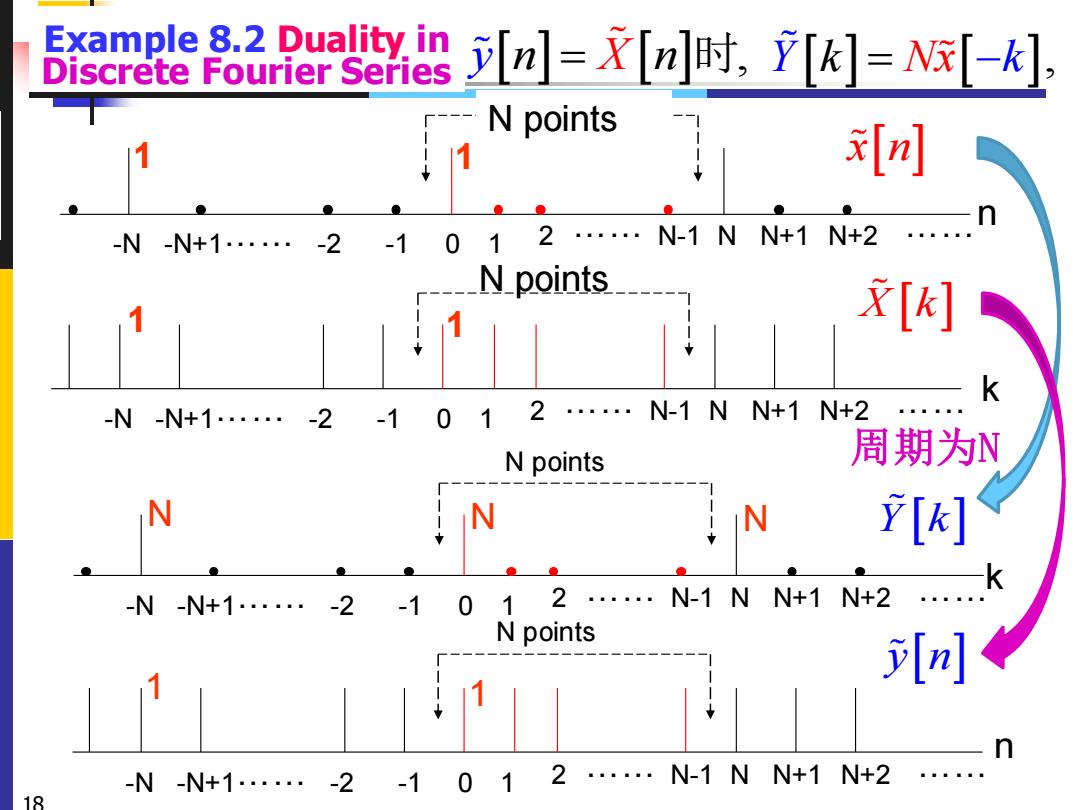
Example 8.2 Duality in Discrete Fourier Series n]=[n]时,[k]=[-] N points 7 [川 -N-N+1·-2-101 2 ·N-1NN+1N+2 Npoints x[灯 -N-N+1·-2-101 2·N-1N N+1N+2 N points 周期为N N N N [k] -N-N+1·-2-10 1 2 .·N-1NN+1N+2 N points [ n -N-N+1·-2 2 -101 ··N-1NN+1N+2 18
18 k X k 0 1 -N -N+1…… -2 -1 2 …… N-1 N N+1 N+2 …… N points 1 1 0 1 -N -N+1…… -2 -1 2 …… N-1 N N+1 N+2 …… N points N N N Y k y n 0 1 -N -N+1…… -2 -1 2 …… N-1 N N+1 N+2 …… N points 1 1 n 0 1 -N -N+1…… -2 -1 2 …… N-1 N N+1 N+2 …… N points 1 1 x n Example 8.2 Duality in Discrete Fourier Series k n yn = X n时, Y k k = Nx− , 1 0 2 1 [ ] N k j kn N x n X k N e − = = 周期为N

Example 8.3 The Discrete Fourier Series of a Periodic Rectangular Pulse Train Periodic sequence with period N=10 n] 1 11 -10 012345678910 Solution:9 []=∑W 1-W8_1-e5k21o0 1-W踏 1-ek(2π10 Wo-e n=0 ejk(π1o)eI5kπ1o)-ej5k(π/1o) =ej4πko)sin(πk/2) eJk(a10ekro,-ek(π1o sin(πk/10) 10 W-1
19 Example 8.3 The Discrete Fourier Series of a Periodic Rectangular Pulse Train ◆Periodic sequence with period N=10 5 10 10 1 1 k k W W − = − 0 4 10 = = kn n X k W ( ) ( ) ( ) 4 10 sin 2 sin 10 j k k k e − = 1 Solution: 10 2 10 j W e − = ( ) ( ) ( ) ( ) ( ) ( ) 10 10 10 10 10 10 j j j 5 5 5 j j j k k k k k k e e e e e e − − − − − = − ( ) ( ) 2 10 2 10 5 1 1 jk j k e e − − − = − x n 9 9 1 0 1 N kn N k x n X k W N − − = = DFS 1 0 N kn N n X k x n W − = = 1 0 1 2 3 4 1 5
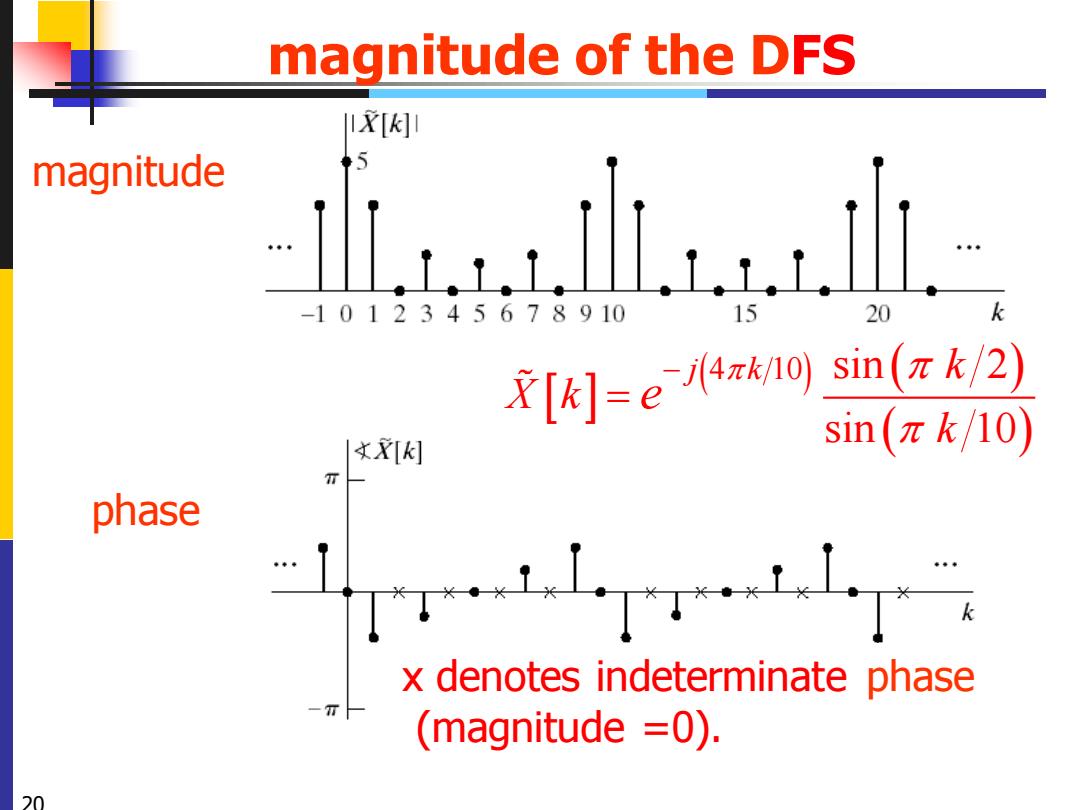
magnitude of the DFS IX[k]1 magnitude -a 5 -1012345678910 20 文[k 1-ea”编 sin(πk/10) T phase x denotes indeterminate phase (magnitude =0). 20
20 magnitude of the DFS magnitude phase x denotes indeterminate phase (magnitude =0). ( ) ( ) ( ) 4 10 sin 2 sin 10 − = j k k X k k e