2021/11/4 固体材料热膨胀机理 ·固体材料的热膨胀本质,归结为点阵结 构中的质点间平均距离随温度升高而增 大。 ·原子在平衡位置两侧,受力并不对称。 在平衡位置。的两侧, 曲线的 率较大斥力位移增大得相对地快 斜率较小 引力随位移的增大 要些这致热振动时均位 诉力胞 不左。 而要向右移。温度越高,右移 越多导致热膨胀 图38品体电质点间 力斥力曲线和位能曲线 固体材料热膨胀机理 ·升温时,原子在平衡位置附近振动。 在T时原子在 b间振动。其平均位 置在A点 当继续升温时」 平均位置沿 着A-B移动,导致热膨胀 ·在热振动时,某一原子的能量为为 Vro+δ,δ为偏离平衡位置的距离(δ <r,则 V() 其中,-,到 西3华束夜有接商商对所 ·对于热容,可只考虑到第二项,即 Vo=r()+2 P=一=一脑 11
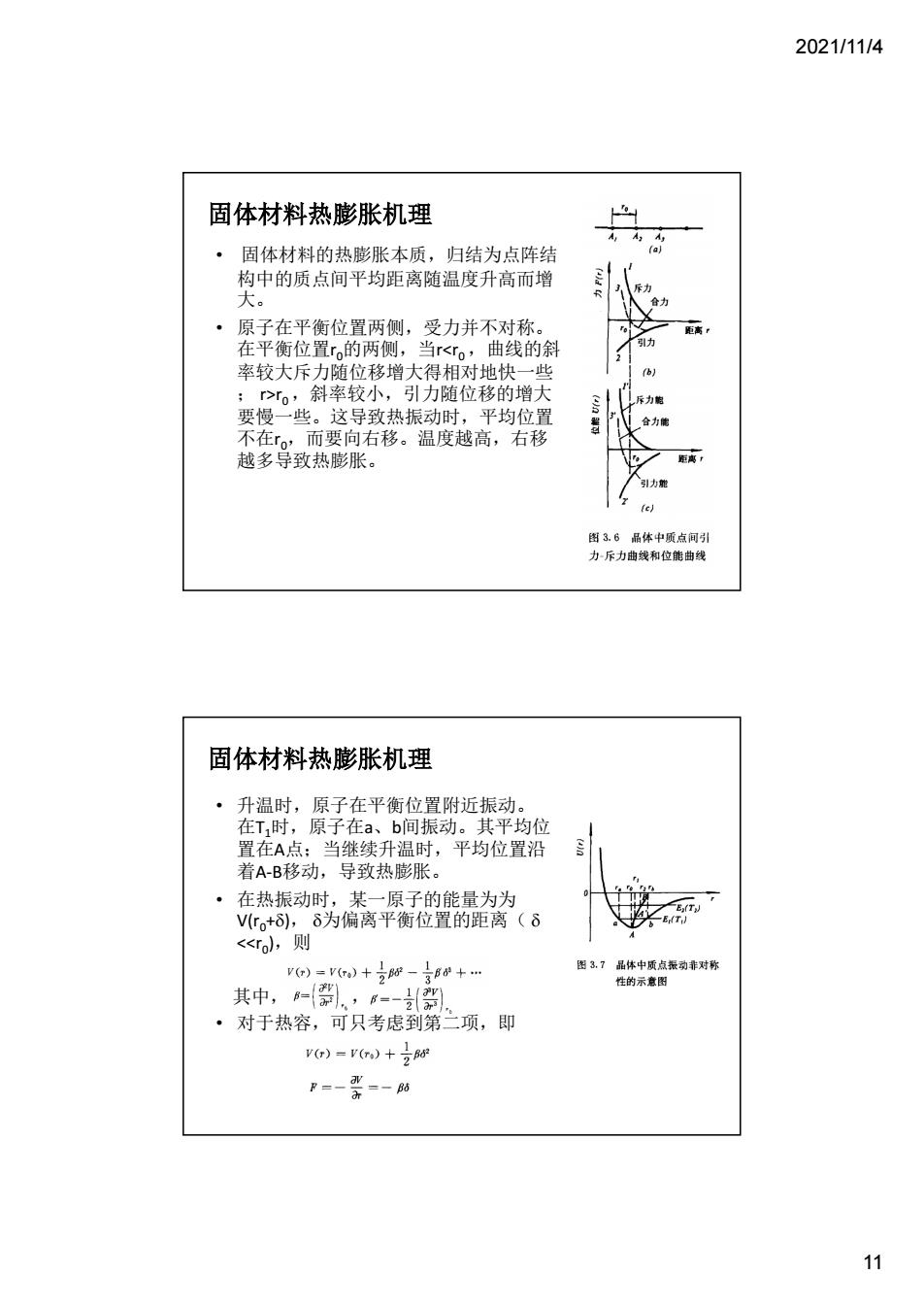
2021/11/4 11 • 固体材料的热膨胀本质,归结为点阵结 构中的质点间平均距离随温度升高而增 大。 • 原子在平衡位置两侧,受力并不对称。 在平衡位置r0 的两侧,当r<r0 ,曲线的斜 率较大斥力随位移增大得相对地快一些 ; r>r0 ,斜率较小,引力随位移的增大 要慢一些。这导致热振动时,平均位置 不在r0 ,而要向右移。温度越高,右移 越多导致热膨胀。 固体材料热膨胀机理 • 升温时,原子在平衡位置附近振动。 在T1 时,原子在a、b间振动。其平均位 置在A点;当继续升温时,平均位置沿 着A-B移动,导致热膨胀。 • 在热振动时,某一原子的能量为为 V(r0 +), 为偏离平衡位置的距离( <<r0 ),则 其中, , • 对于热容,可只考虑到第二项,即 固体材料热膨胀机理

2021/11/4 固体材料热膨胀机理 ·萃钙热警务需买座前三项热报动为非线性振动。其 ·膨胀系数可表达为 ·如果讨论膨胀系数随温度的变化,还须考虑更高次项。 ·简谐振动不产生热膨胀 ·除了晶格振动,品体中各种热缺陷的形成将造成局部点阵 的畸变和膨胀,也可以导致热膨胀,但随着温度的升高, 热缺陷浓度呈指数增加,在高温时,这方面的影响对某些 晶体也就变得重要了。 热膨胀与其他性能的关系 ·热膨胀和结合能、熔点的关系:于固体材料的热膨胀与晶 体点阵中质点的位能性质有关。质点的位能性质是由质点 间的结合力特性所决定的。质点间结合力很强,则位阱深 而狭窄,升高同样的温度差,质点振幅增加得较少,故平 均位置的位移量增加得较少,因此,热膨胀系数较小。 表3.2 单质材料(10-m)结合腰(×10/mD熔点(C)a(×10-) 金刚石 712. 12
2021/11/4 12 • 对于热膨胀,需要考虑前三项,热振动为非线性振动。其 平均位置为 • 膨胀系数可表达为 • 如果讨论膨胀系数随温度的变化,还须考虑更高次项。 • 简谐振动不产生热膨胀 • 除了晶格振动,晶体中各种热缺陷的形成将造成局部点阵 的畸变和膨胀,也可以导致热膨胀,但随着温度的升高, 热缺陷浓度呈指数增加,在高温时,这方面的影响对某些 晶体也就变得重要了。 固体材料热膨胀机理 • 热膨胀和结合能、熔点的关系:于固体材料的热膨胀与晶 体点阵中质点的位能性质有关。质点的位能性质是由质点 间的结合力特性所决定的。质点间结合力很强,则位阱深 而狭窄,升高同样的温度差,质点振幅增加得较少,故平 均位置的位移量增加得较少,因此,热膨胀系数较小。 热膨胀与其他性能的关系

2021/1114 热膨胀与其他性能的关系 表达为 -告=产岩-六 ·温度越高,膨胀系数增加。 ·热膨胀是固体材料受热以后品格振动 tgf-ca 加剧而引起的容积膨胀,而品格振动 的激化就是热运动能量的增大。升高 单位温度时能量的增量也就是热容的 奢希相被囊数与热容密切相天并 低温下, 高温下,缺陷的贡献使α增加。 热膨胀与其他性能的关系 热膨胀和结构的关系:对于相同组成的 物质 结构不同 系数也不同。通 系数较 定形的玻盘.奥往有较小的 ~瓦黄的膨张系数1210K,石英玻瑞05x10 离美视文翁地整锁配内部的空隙所容纳 图3102r0的热张曲线 .+mol 由于温度变化时发生晶型转换,也会引 起体积变化。比如zrO, 因为材料的各向异性,会使整体的α值 为负值,在陶瓷材料中α低的有革青石 石、钡长石及硅酸铝等。 13
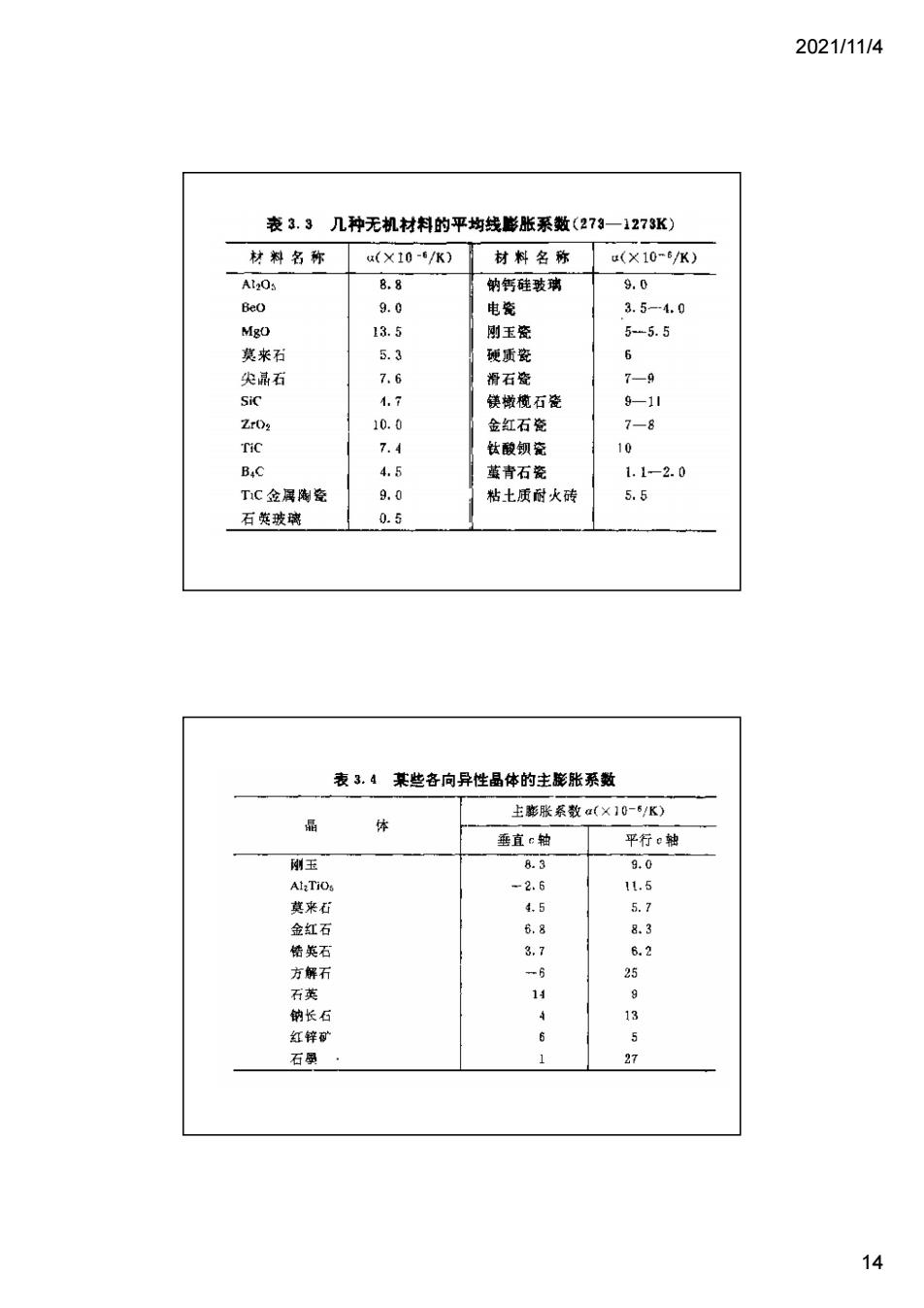
2021/11/4 13 • 热膨胀与温度、热容的关系:热膨胀 系数与图中的A-B曲线的斜率有关。可 表达为 • 温度越高,膨胀系数增加。 • 热膨胀是固体材料受热以后晶格振动 加剧而引起的容积膨胀,而晶格振动 的激化就是热运动能量的增大。升高 单位温度时能量的增量也就是热容的 定义。热膨胀系数与热容密切相关并 有着相似的规律。 • 两种性质随温度变化曲线近于平行, 变化趋势相同。低温下,趋近于0; 高温下,缺陷的贡献使增加。 热膨胀与其他性能的关系 • 热膨胀和结构的关系:对于相同组成的 物质,结构不同,膨胀系数也不同。通 常结构紧密的晶体,膨胀系数较大,而 类似于无定形的玻璃,则往往有较小的 膨胀系数。 – 石英的膨胀系数1210-6/K,石英玻璃0.510- 6 /K。 – 主要原因玻璃玻璃的结构较琉松,内部空隙 较多,温度升高,原子振幅加大,原子间距 离增加时,部分地被结构内部的空隙所容纳 ,表现出较低的膨胀系数。 • 由于温度变化时发生晶型转换,也会引 起体积变化。比如ZrO2 • 因为材料的各向异性,会使整体的值 为负值,在陶瓷材料中低的有堇青石 石、钡长石及硅酸铝等。 热膨胀与其他性能的关系
2021/11/4 表3.3几种无机材料的平均线影胀系数(273一1273K) 材料名称 u(X10-6/K) 材料名称 u(X10-6K) B. 0 9.0 电瓷 3.5-4.0 Mgo 13.5 刚玉瓷 5-5.5 莫来石 硬质瓷 6 尖石 滑石瓷 79 S 快橄榄石瓷 9-11 Zro 10.0 金红石 7-8 7.4 10 粘土质耐火砖 石玻璃 表3,4某些各向异性品体的主影张系数 主整张系数a(X10-/K) 垂直c柏 平行0袖 玉 8.3 9.0 -2.6 1l.5 93- 石 14
2021/11/4 14

2021/11/4 多晶体和复合材料的热膨胀 ·如果晶体是各向异性的,或复合材料中各相的膨胀系数不 相,则它们在烧成后的冷却过程中产生内应力。 ·对活组务含树整备架鞋穷含向同作,升温时产生内应力 a=k(av-a.)AT 模量:=300 ·总体的应力为零,即2-∑xa-4w-g V,为第组成的体积分数。 多晶体和复合材料的热膨胀 ·若W,为第组分的重量百分比则 V=WIp ·则体膨胀系数可表达为 a-xw/a 云=R ·以上推导微观的内应力都看成是纯拉应力 和压应力,对交界面上的剪应力不考虑。 若计入剪应力的影响,对于为二相材料的 热膨胀系数(G为剪切模量)为 网a,+(2-) 15
2021/11/4 15 • 如果晶体是各向异性的,或复合材料中各相的膨胀系数不 相,则它们在烧成后的冷却过程中产生内应力。 • 对于一复合材料,各组分为各向同性,升温时产生内应力 ,各组分的内应力可表达为 其中 为复合体的平均体积膨胀系数,i 为第i组成的体膨 胀系数,T为应力松弛状态算起的温度变化。K为体弹性 模量: • 总体的应力为零,即 Vi 为第i组成的体积分数。 多晶体和复合材料的热膨胀 v • 若Wi 为第i组分的重量百分比则 • 则体膨胀系数可表达为 • 以上推导微观的内应力都看成是纯拉应力 和压应力,对交界面上的剪应力不考虑。 若计入剪应力的影响,对于为二相材料的 热膨胀系数(Gi 为剪切模量)为 多晶体和复合材料的热膨胀 / V W i i i