消息空间 信号空间 观察空间 判决空间 判决 X S 规则 n 噪声空间 数字信号接收的统计模型 消息空间、信号空间、噪声空间、观察空间及判决空间分别 代表消息、信号、噪声、接收波形及判决的所有可能状态的 集合
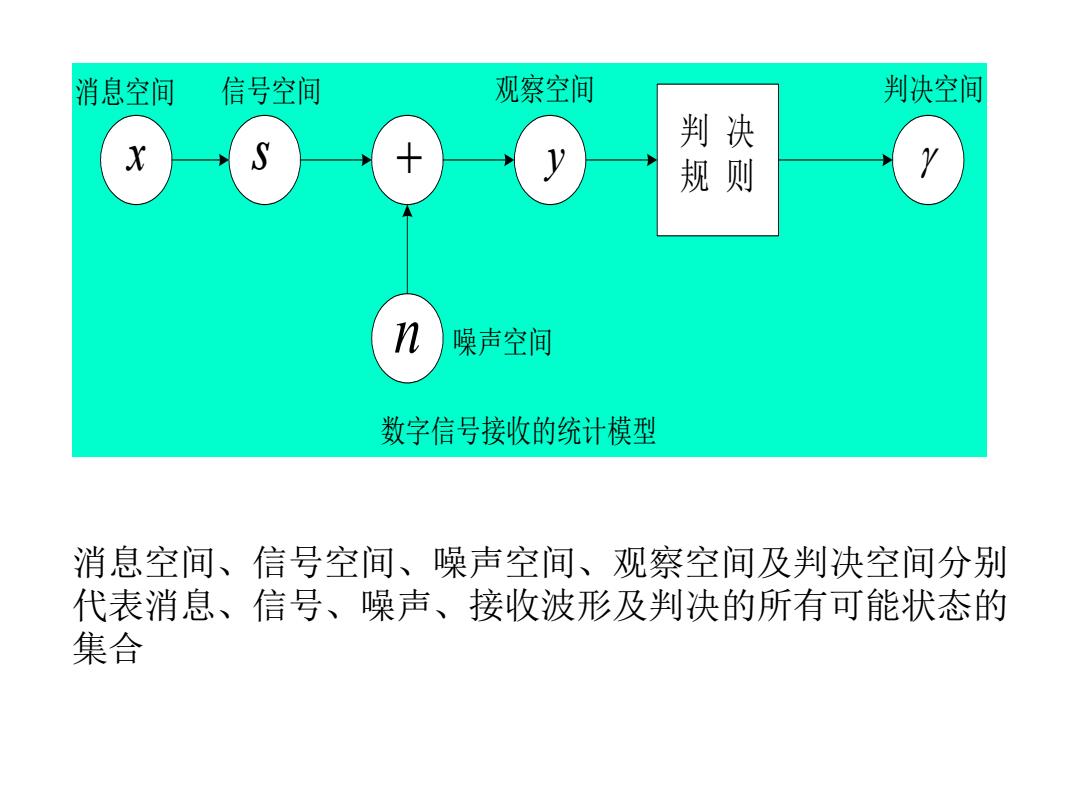
x s + y n 判 决 规 则 消息空间 信号空间 观察空间 判决空间 噪声空间 数字信号接收的统计模型 消息空间、信号空间、噪声空间、观察空间及判决空间分别 代表消息、信号、噪声、接收波形及判决的所有可能状态的 集合

在数字通信系统中,消息是离散的状态,设消息的 状态集合为 X={x1,X2,,xm} 若消息集合中每一状态的发送是统计独立的,第个 状态x的出现概率为P(x), 则消息X的一维概率分布为 Xj X2 Xm P(X1)P(X2). P(Xm) 根据概率的性质有 ∑p(x)=1
在数字通信系统中, 消息是离散的状态, 设消息的 状态集合为 X={x1 , x2 , …, xm} 若消息集合中每一状态的发送是统计独立的, 第i个 状态xi的出现概率为P(xi ), 则消息X的一维概率分布为 X1 x2 … xm P(x1 ) P(x2 ) … P(xm) 根据概率的性质有 1 ( ) 1 m i i p x = =

若消息各状态x1,x2,,Xm出现的概率相等,则有 1 P(x)=P(x2)=…=P(xm)= m 消息是各种物理量,本身不能直接在数字通信系统 中进行传输 因此 需要将消息变换为相应的电信号s(),用参数$来表示
若消息各状态x1 , x2 , …, xm出现的概率相等,则有 1 2 1 ( ) ( ) ( ) P x P x P xm m = = = = 消息是各种物理量, 本身不能直接在数字通信系统 中进行传输 需要将消息变换为相应的电信号s(t),用参数S来表示。 因此

将消息变换为信号可以有各种不同的变换关系, 通常最直接的方法是建立消息与信号之间一一对 应的关系,即消息x与信号s(=1,2,,m)相对 应。 这样,信号集合S也由m个状态所组成 即 S={S1,S2,,Sm}
将消息变换为信号可以有各种不同的变换关系, 通常最直接的方法是建立消息与信号之间一一对 应的关系,即消息xi与信号si (i=1, 2, …, m)相对 应。 这样,信号集合S也由m个状态所组成 即 S={s1 , s2 , …, sm}

并且信号集合各状态出现概率与消息集合各状 态出现概率相等,即 P(s)=P(x) P(S2)=P(x2) P(Sm)=P(xm) 同时也有 ∑ps,)=1 i1
并且信号集合各状态出现概率与消息集合各状 态出现概率相等,即 1 1 2 2 ( ) ( ) ( ) ( ) P s P x P s P x = = ( ) ( ) P s P x m m = . . . 同时也有 = = n i i p s 1 ( ) 1