
=a-台 (e≤eo) (3-2) 式中0。为峰值应力。CEP.P规范取o-0.85k,:为混凝土标准圆柱体抗压强度, 0.85为折减系数。同时,CEP-FIP规范取:0.002 图3-15中直线段AB为水平线,应力0=00,B点的应变c=0.0035,cm为混凝土极 限压应变。 (2)钢筋的应力应变曲线,多采用简化的理想弹塑性应力应变关系(图3-16)。对于 有明显屈服台阶的钢筋,OA为弹性阶段,A点对应的应力为钢筋屈服强度·,相应的应 变为屈服应变c,OA的斜率为弹性模量E。AB为塑性阶段,B点对应的应变为强化段开 始的应变:,由(图3-6)可得到普通钢筋的应力应变关系表达式为 0=EsE:(0≤6s5Ev】 (3-3) 0=0y(e,>e) (3-4) A 6 图3-15CEB一FP标准规范采用的混凝士 图3-16钢筋应力应变曲线模式图 应力应变曲线模式图 式(33)中钢筋应力取等于钢筋应变与弹性模量的乘积,但其绝对值不大于相应的强 度设计值。对钢筋混凝土受弯构件进行正截面承载力计算时,钢筋的应力-应变关系可以采 用弹性全塑性曲线:在钢筋受拉屈服之前,钢筋应力和应变成正比:钢筋受拉屈服后,钢 筋应力保持不变。同时,《公路桥规》规定纵向钢筋的受拉极限应变为Q.01,这也是构件 到承载能力极限状态的标志之一,实际上限制了钢筋的强化强度以保证结构构件具有必要 的延性。 3.3.2压区混凝土等效矩形应力图形 钢筋混凝土受弯构件正截面承载力M。的计算前提是要知道破坏时混凝土压应力的分 布图形,特别是压区混凝土的压应力合力C及其作用位置(图3-17) 图317受压区混凝土等效矩形应力图 )截面b)平均应变分布c压区混凝土应力分布模式d)等效矩形混凝土压应力分布 钢筋混凝土梁正截面破坏时混凝土压应力的分布图形与混凝土的应力应变曲线(受压 时)是相似的,现取图子15所示的混凝土应力应变曲线模式图,即当≤。时 山
3-11 2 0 0 0 2( ) ( ) = − (ε≤ε0) (3-2) 式中σ0 为峰值应力。CEP-FIP 规范取σ0=0.85fck,fck 为混凝土标准圆柱体抗压强度, 0.85 为折减系数。同时,CEP-FIP 规范取ε0=0.002。 图 3-15 中直线段 AB 为水平线,应力σ=σ0,B 点的应变εcu=0.0035,εcu 为混凝土极 限压应变。 (2)钢筋的应力应变曲线,多采用简化的理想弹塑性应力应变关系(图 3-16)。对于 有明显屈服台阶的钢筋,OA 为弹性阶段,A 点对应的应力为钢筋屈服强度σy,相应的应 变为屈服应变εy,OA 的斜率为弹性模量 Es。AB 为塑性阶段,B 点对应的应变为强化段开 始的应变εk,由(图 3-16)可得到普通钢筋的应力应变关系表达式为 σs=εsEs (0≤εs≤εy) (3-3) σs=σy (εs>εy) (3-4) = α α = [ ( ) ] 图 3-15 CEB-FIP 标准规范采用的混凝土 图 3-16 钢筋应力应变曲线模式图 应力应变曲线模式图 式(3-3)中钢筋应力取等于钢筋应变与弹性模量的乘积,但其绝对值不大于相应的强 度设计值。对钢筋混凝土受弯构件进行正截面承载力计算时,钢筋的应力-应变关系可以采 用弹性-全塑性曲线:在钢筋受拉屈服之前,钢筋应力和应变成正比;钢筋受拉屈服后,钢 筋应力保持不变。同时,《公路桥规》规定纵向钢筋的受拉极限应变为 0.01,这也是构件达 到承载能力极限状态的标志之一,实际上限制了钢筋的强化强度以保证结构构件具有必要 的延性。 3.3.2 压区混凝土等效矩形应力图形 钢筋混凝土受弯构件正截面承载力 Mu 的计算前提是要知道破坏时混凝土压应力的分 布图形,特别是压区混凝土的压应力合力 C 及其作用位置 yc(图 3-17)。 ) ) ) ) = σ γ = = 图 3-17 受压区混凝土等效矩形应力图 a)截面 b)平均应变分布 c)压区混凝土应力分布模式 d)等效矩形混凝土压应力分布 钢筋混凝土梁正截面破坏时混凝土压应力的分布图形与混凝土的应力应变曲线(受压 时)是相似的,现取图 3-15 所示的混凝土应力应变曲线模式图,即当ε≤ε 0 时

口=02会-(学当>,时,=0而-,的点距中和轴的距离为州国 3-17b)1。 由平截面假定可得到混凝土受压区高度x=5h[图3-17c)],同样得到e/e,及 V=605cho/Ece 现以图317所示的矩形截面,米推导破坏时压区混凝土的压应力合力C及其合力作用 位置必的表达式。 压区混凝土的应力应变曲线为两段,须分段积分才能得到压应力合力C为 C=o(e)bdy -r[店-海+ 注意到e1e,及=h加,积分后可得到 E C=a5AM1-是 (3-5) 混凝土压应力合力C的作用点至受压边缘的距离,可由下式计算: C 将式中的积分计算后,可得到 11 上=54122会 (3-6) 显然,用混凝士受压时的应力应变曲线=0(©)米求应力合力C和合力作用点北是比 较麻烦的。因此,为了计算方便起见 可以设想在保持压应力合力C的大小及其作用位置 不变条件下,用等效矩形的混凝土压应力图图3-17d)]来替换实际的混凝土压应力分布 图形[图3-17c)]。这个等效的矩形压应力图形由无量纲参数B和y确定。B为矩形压应 力图的高度x与按平截面假定的中和轴高度x的比值,即B=x:y为矩形压应力图的应 力与受压区混凝土最大应力o0的比值[图3-17d)]。 在图3-17)中可得到等效矩形压应力图形的合力C为 C=yobr=yob。=yBab5h (3-7) 合力C的作用位置y为 3-12
3-12 2 0 0 0 2( ) ( ) = − ;当ε>ε0 时,σ=σ0,而ε=ε0 的点距中和轴的距离为 y0[图 3-17b)]。 由平截面假定可得到混凝土受压区高度 xc=ξch0[图 3-17c)],同样得到ε/ε0=y/y0,及 y0=ε0ξch0/εcu。 现以图 3-17 所示的矩形截面,来推导破坏时压区混凝土的压应力合力 C 及其合力作用 位置 yc的表达式。 压区混凝土的应力应变曲线为两段,须分段积分才能得到压应力合力 C 为 ( ) 0 0 0 0 0 2 0 0 0 0 0 2 ( ) c c h y h y C bdy bdy bdy = = − + 注意到ε/ε0=y/y0,及 y0= cu 0 ξch0,积分后可得到 0 0 0 1 (1 ) 3 c cu C h b = − (3-5) 混凝土压应力合力 C 的作用点至受压边缘的距离 yc,可由下式计算: ( ) C bydy y h h c c c = − 0 0 0 将式中的积分计算后,可得到 0 2 0 0 1 1 ( ) 2 12 1 1 1 3 cu c c cu y h − = − − (3-6) 显然,用混凝土受压时的应力应变曲线σ=σ(ε)来求应力合力 C 和合力作用点 yc是比 较麻烦的。因此,为了计算方便起见,可以设想在保持压应力合力 C 的大小及其作用位置 yc不变条件下,用等效矩形的混凝土压应力图[图 3-17d)]来替换实际的混凝土压应力分布 图形[图 3-17c)]。这个等效的矩形压应力图形由无量纲参数 和 确定。 为矩形压应 力图的高度 x 与按平截面假定的中和轴高度 xc的比值,即 =x/xc; 为矩形压应力图的应 力与受压区混凝土最大应力σ0 的比值[图 3-17d)]。 在图 3-17d)中可得到等效矩形压应力图形的合力 C 为 0 0 0b h0 C bx b xc c = = = (3-7) 合力 C 的作用位置 yc为

y.= (3-8) 根据等代原则:压应力合力C不变,即式(35)等于式(3-7):压应力合力位置 不变,即式(3-6)等于式(3-8)。解含有求知数B和y的联立方程,可得到 -2+ B= (3-9) 036 (3-10) 当确定c、£值后,即可将图317c)的压区混凝土实际压应力分布图,换成等效的 矩形压应力分布图形 若取c0.002,混凝土极限压应变8=-0.0033,而不是按CEB-FP那样取8m=0.0035。 由式(3-9)和式(3-10)可得到B=0.8095,Y-0.9608,即等效矩形压应力图形高度x0.8095x 等效压应力值为y000.960800。 对于受弯构件截面受压区边缘混凝土的极限压应变和相应的系数B,《公路桥规》 按混凝土强度级别来分别取值,详见表31。基于上述受压区混凝土应力计算图形采用等效 矩形图形的分析,结合国内外试验资料,《公路桥规》对所取用的混凝土受压区等效矩形应 力值取yo。,a为混凝土的轴心抗压强度设计值。 混凝土极限压应变6与系数B值 表3-1 00330.032500200315003100305003 B 04 3.3.3相对界限受压区高度5。 当钢筋混凝土梁的受拉区钢筋达到屈服应变¢,而开始屈服时,受压区混凝土边缘也同 时达到其极限压应变:,而破坏,此时被称为界限破坏。 根据给定的 和平截面假定可以做出如图3-18所示截面应变分布的直线。 ,这就是 梁截面发生界限破坏的应变分布。受压区高度为一5,56被称为相对界限混凝土受压 区高度。 适筋截面受弯构件破坏始于受拉区钢筋屈服,经历一段变形过程后压区边缘混凝土达 到极限压应变cm后才破坏,而这时受拉区钢筋的拉应变c,>c,由此可得到适筋截面破 坏时的应变分布如图3-8中的ac直线。此时受压区高度x 超筋裁面受弯枸件 压区边缘混凝 到极限压 不,这时 拉区钢 筋的拉应变:,<e,由此可得到超筋截面破坏时的应变分布如图3-18中的ad直线,此时 3
3-13 c 0 2 1 2 1 2 y x h x = = c = c (3-8) 根据等代原则:压应力合力 C 不变,即式(3-5)等于式(3-7);压应力合力位置 yc 不变,即式(3-6)等于式(3-8)。解含有求知数 和 的联立方程,可得到 ) 3 1 (1 ( ) 6 1 ( ) 3 2 1 0 0 0 2 cu cu cu − − + = (3-9) ) 3 1 (1 1 0 cu = − (3-10) 当确定ε0、 cu 值后,即可将图 3-17c)的压区混凝土实际压应力分布图,换成等效的 矩形压应力分布图形。 若取ε0=0.002,混凝土极限压应变 cu =0.0033,而不是按 CEB-FIP 那样取 cu =0.0035。 由式(3-9)和式(3-10)可得到β=0.8095,γ=0.9608,即等效矩形压应力图形高度 x=0.8095xc, 等效压应力值为 σ0=0.9608σ0。 对于受弯构件截面受压区边缘混凝土的极限压应变εcu 和相应的系数 ,《公路桥规》 按混凝土强度级别来分别取值,详见表 3-1。基于上述受压区混凝土应力计算图形采用等效 矩形图形的分析,结合国内外试验资料,《公路桥规》对所取用的混凝土受压区等效矩形应 力值取 0 =fcd,fcd 为混凝土的轴心抗压强度设计值。 混凝土极限压应变 cu 与系数 值 表 3-1 混凝土强度等级 C50 以下 C55 C60 C65 C70 C75 C80 cu 0.0033 0.00325 0.0032 0.00315 0.0031 0.00305 0.003 0.8 0.79 0.78 0.77 0.76 0.75 0.74 3.3.3 相对界限受压区高度ξb 当钢筋混凝土梁的受拉区钢筋达到屈服应变εy而开始屈服时,受压区混凝土边缘也同 时达到其极限压应变εcu 而破坏,此时被称为界限破坏。 根据给定的εcu 和平截面假定可以做出如图 3-18 所示截面应变分布的直线 ab,这就是 梁截面发生界限破坏的应变分布。受压区高度为 xb=ξbh0,ξb 被称为相对界限混凝土受压 区高度。 适筋截面受弯构件破坏始于受拉区钢筋屈服,经历一段变形过程后压区边缘混凝土达 到极限压应变εcu 后才破坏,而这时受拉区钢筋的拉应变εs>εy,由此可得到适筋截面破 坏时的应变分布如图 3-18 中的 ac 直线。此时受压区高度 xc<ξbh0。 超筋截面受弯构件破坏是压区边缘混凝土先达到极限压应变εcu 破坏,这时受拉区钢 筋的拉应变εs<εy,由此可得到超筋截面破坏时的应变分布如图 3-18 中的 ad 直线,此时
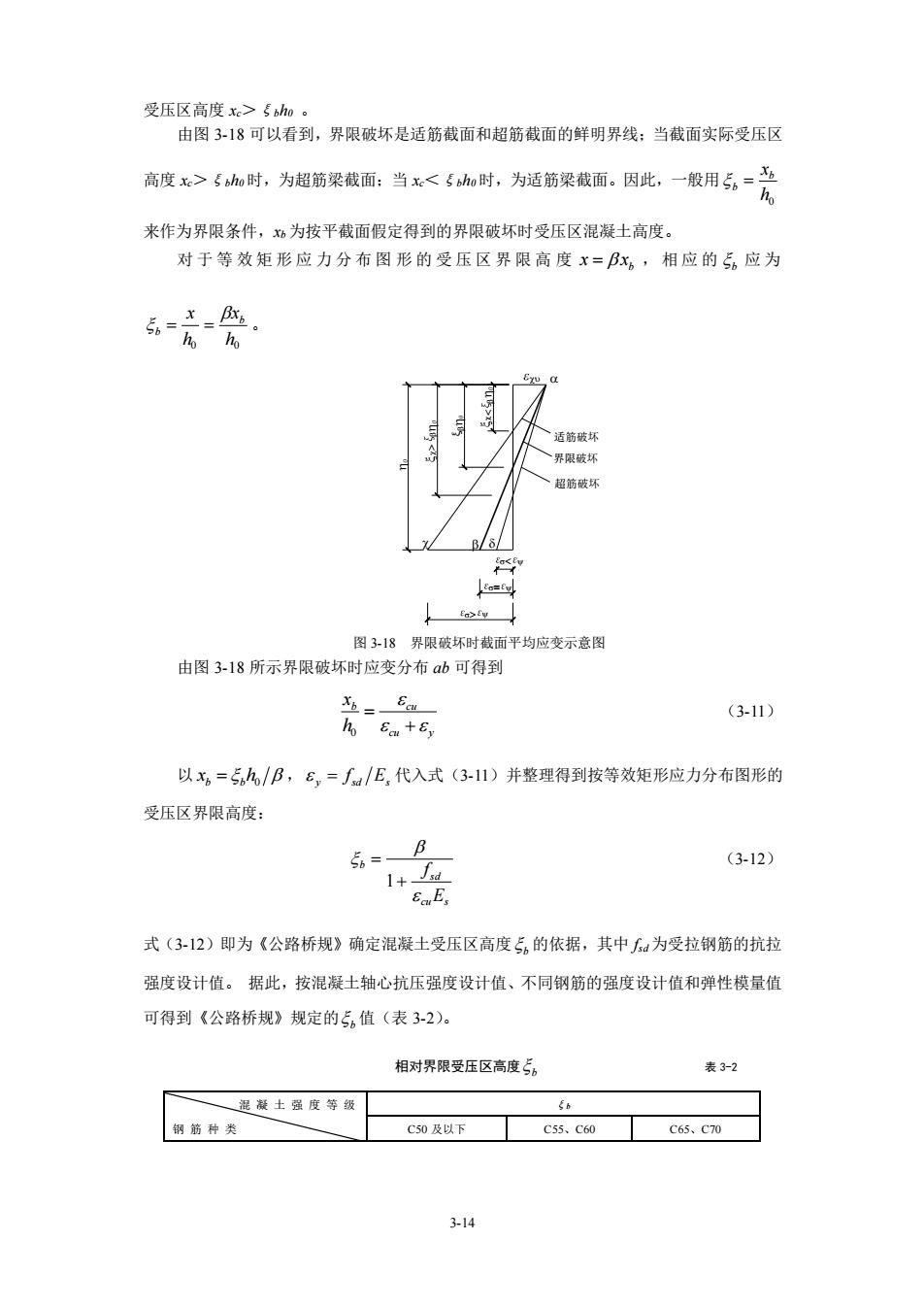
受压区高度x>5h加。 由图318可以看到,界限破坏是适筋截面和超筋截面的鲜明界线:当截面实际受压区 高度x>5时,为超筋梁截面:当x<5h时,为适筋梁截面。因此,一般用5=产 来作为界限条件,场为按平截面假定得到的界限破坏时受压区混凝土高度。 对于等效矩形应力分布图形的受压区界限高度x=Bx,相应的5应为 ↓ 图318界限破坏时截而平均应变示意图 由图3-18所示界限破坏时应变分布b可得到 £u (3-11) 以x。-5h/B,6,-∫/E,代入式(3-11)并整理得到按等效矩形应力分布图形的 受压区界限高度: 5=-B (3-12) 1+ EaE: 式(312)即为《公路桥规》确定混凝土受压区高度5的依据,其中为受拉钢筋的抗拉 强度设计值。据此,按混凝士轴心抗压强度设计值、不同钢筋的强度设计值和弹性模量值 可得到《公路桥规》规定的。值(表3-2)。 相对界限受压区高度5 表3-2 一退凝士强度等级 C50及以下 c5.c60c65.C0 314
3-14 受压区高度 xc>ξbh0 。 由图 3-18 可以看到,界限破坏是适筋截面和超筋截面的鲜明界线;当截面实际受压区 高度 xc>ξbh0 时,为超筋梁截面;当 xc<ξbh0 时,为适筋梁截面。因此,一般用 h0 xb b = 来作为界限条件,xb 为按平截面假定得到的界限破坏时受压区混凝土高度。 对 于 等效矩形应力分布图形的受压区界限高度 b x x = ,相应的 b 应 为 0 h0 x h x b b = = 。 界限破坏 超筋破坏 适筋破坏 ξ = 图 3-18 界限破坏时截面平均应变示意图 由图 3-18 所示界限破坏时应变分布 ab 可得到 cu y b cu h x + = 0 (3-11) 以 b b 0 x h = , y sd s = f E 代入式(3-11)并整理得到按等效矩形应力分布图形的 受压区界限高度: cu s sd b E f + = 1 (3-12) 式(3-12)即为《公路桥规》确定混凝土受压区高度 b 的依据,其中 fsd 为受拉钢筋的抗拉 强度设计值。 据此,按混凝土轴心抗压强度设计值、不同钢筋的强度设计值和弹性模量值 可得到《公路桥规》规定的 b 值(表 3-2)。 相对界限受压区高度 b 表 3-2 混 凝 土 强 度 等 级 钢 筋 种 类 ξb C50 及以下 C55、C60 C65、C70

R235 062 0.60 0.58 HRB335 0.56 0.54 0.52 1HRB400.K1400 0.53 051 0.49 而受拉区内配置不种类锅的受弯构件,其5值应选用相应于各种箭的较小者。 3.3.4最小配筋率pm 为了避免少筋梁破坏,必须确定钢筋混凝土受弯构件的最小配筋率 最小配筋率是少筋梁与适筋梁的界限 当梁的配筋率由 P 逐渐减少,梁的工作特性 也从钢筋混凝士结构逐渐向素混凝土结构过渡,所以,P可按采用最小配筋率P的钢 筋混凝土梁在破坏时,正截面承载力M等于同样截面尺寸、同样材料的素混凝土梁正截面 开裂弯矩标淮值的原则确定。 由上述原则的计算结果,同时考虑到温度变化、混凝土收缩应力的影响以及过去的设 计经验,《公路桥规》规定了受弯构件纵向受力钢筋的最小配筋率P(),详见附表19。 3.4单筋矩形截面受弯构件 3.4.1基本公式及适用条件 根据受弯构件正截面承载力计算的基本原则,可以得到单筋矩形截面受弯构件承载力 计算简图(图319)。 X=dB 图319单筋矩形截面受弯构件正截而承截力计算图式 按照第2章所述钢筋混凝土结构设计计算基本原则,在受弯构件计算截面上的最不利 荷载基本组合效应计算值YM不应超过截面的承载能力(抗力)M 由图319可以写出单筋矩形截面受弯构件正截面计算的基本公式。 由截面上水平方向内力之和为零的平衡条件,即T+C=0,可得到 foubx =fA, (3-13) 由截面上对受拉钢筋合力T作用点的力矩之和等于零的平衡条件,可得到 oM,≤M.=f.bx(h,-2 (3-14 由对压区混凝士合力C作用点取力矩之和为零的平衡条件,可得到 YoMa≤M.=fa4,h- (3-15) 式中M一一计算截面上的弯矩组合设计值 。一一结构的重要性系数: 315
3-15 R235 0.62 0.60 0.58 HRB335 0.56 0.54 0.52 HRB400,KL400 0.53 0.51 0.49 注:截面受拉区内配置不同种类钢筋的受弯构件,其ξb 值应选用相应于各种钢筋的较小者。 3.3.4 最小配筋率 min 为了避免少筋梁破坏,必须确定钢筋混凝土受弯构件的最小配筋率ρmin。 最小配筋率是少筋梁与适筋梁的界限。当梁的配筋率由ρmin 逐渐减少,梁的工作特性 也从钢筋混凝土结构逐渐向素混凝土结构过渡,所以,ρmin 可按采用最小配筋率ρmin 的钢 筋混凝土梁在破坏时,正截面承载力 Mu 等于同样截面尺寸、同样材料的素混凝土梁正截面 开裂弯矩标准值的原则确定。 由上述原则的计算结果,同时考虑到温度变化、混凝土收缩应力的影响以及过去的设 计经验,《公路桥规》规定了受弯构件纵向受力钢筋的最小配筋率 (%) min ,详见附表 1-9。 3.4 单筋矩形截面受弯构件 3.4.1 基本公式及适用条件 根据受弯构件正截面承载力计算的基本原则,可以得到单筋矩形截面受弯构件承载力 计算简图(图 3-19)。 = = γ = = 图 3-19 单筋矩形截面受弯构件正截面承载力计算图式 按照第 2 章所述钢筋混凝土结构设计计算基本原则,在受弯构件计算截面上的最不利 荷载基本组合效应计算值γoMd 不应超过截面的承载能力(抗力)Mu。 由图 3-19 可以写出单筋矩形截面受弯构件正截面计算的基本公式。 由截面上水平方向内力之和为零的平衡条件,即 T+C=0,可得到 cd sdAs f bx = f (3-13) 由截面上对受拉钢筋合力 T 作用点的力矩之和等于零的平衡条件,可得到 0Md ≤ ) 2 ( 0 x Mu = f cd bx h − (3-14) 由对压区混凝土合力 C 作用点取力矩之和为零的平衡条件,可得到 0Md ≤ ) 2 ( 0 x Mu = f sd As h − (3-15) 式中 Md——计算截面上的弯矩组合设计值; 0 ——结构的重要性系数;