
试验梁上用油压千斤项施加两个集中荷载F,其弯矩图和剪力图如图39所示。在梁 CD段,剪力为零(忽略梁自重),而弯矩为常数,称为“纯弯曲”段,它是试验研究的主 要对象 试验全衬程要测读荷载常加力值、将度和应变的影据。集中力F大小用刑力传成器别 读:挠度用百分表测量, 设置在试验梁跨中的E点:混凝土应变用标距为200mm的手持 应变仪测读,沿梁跨中截面段的高度方向上布置测点a、b、cd和。 集中力F分级施加。每级加载后,即测读梁的挠度和混凝土应变值。 1)受弯构件正截面工作的三个阶段 图3-10表示试验梁受力全过程中实测的集中力F值与跨中挠度6的关系曲线图,纵向 坐标为力F(kN ,横坐标为跨中挠度w(mm。由图310可见到,当荷载较小时,挠度随 着力F的增加而不断增长,两者基本上成比例:当F≈4.4W时,梁CD段的下部观察到竖 向裂缝,此后挠度就比力F增加得快,并出现了若干条新裂缝:当F≈14.8N时,裂缝急 剧开展,挠度急刷增大:当F≈15.3W时,试验梁截面受压区边缘混凝土被压碎,梁不能 继续负担力℉值而破坏。 纵向钢筋围 图10试验梁的荷载挠度(FP)图 由图310还可以看到,试验梁的F曲线上有两个明显的转折点,从而把梁的受力 和变形全过程分为三个阶段。这三个阶段是:第I阶段,梁没有裂缝:第Ⅱ阶段,梁带有 裂缝工作:第Ⅲ阶段,裂缝急刷开展,纵向受力钢筋应力维持在屈服强度不变。同时试验 梁的F"曲线上有三个特征点,即第1阶段末(用1表示),裂缝即将出现:第Ⅱ阶段末 (用山表示),纵向受力钢筋屈服:第Ⅲ阶段末(用,表示),梁受压区混凝土被压碎, 整个梁截面破坏, 2)梁正截面上的混凝土应力分布规律 图311为试验梁在各级荷载下截面的混凝土应变实测的平均值及相应于各工作阶段截 面上正应力分布图。 由[图3-11a)】可见,随着荷载的增加,应变值也不断增加,但应变图基本上仍是上 下两个对项的三角形。同时还可以看到,随着荷载的增加,中和轴逐渐上升。 在试验中,通过应变仪可以直接测得混凝士的应变和钢筋的应变,要得到截面上的应 力必须从材料的应力-应变关系去推求。图32为试验梁的混凝土和钢筋试件得到的应力 应变鱼线图31b)的应力国是根据图3)的各测点、,测点)的实测 应变值以及图312中材料的应力-应变图,沿截面从上到下, 个测点 个测点地推求出 来的。 6
3-6 试验梁上用油压千斤顶施加两个集中荷载 F,其弯矩图和剪力图如图 3-9 所示。在梁 CD 段,剪力为零(忽略梁自重),而弯矩为常数,称为“纯弯曲”段,它是试验研究的主 要对象。 试验全过程要测读荷载施加力值、挠度和应变的数据。集中力 F 大小用测力传感器测 读;挠度用百分表测量,设置在试验梁跨中的 E 点;混凝土应变用标距为 200mm 的手持 应变仪测读,沿梁跨中截面段的高度方向上布置测点 a、b、c、d 和 e。 集中力 F 分级施加。每级加载后,即测读梁的挠度和混凝土应变值。 1)受弯构件正截面工作的三个阶段 图 3-10 表示试验梁受力全过程中实测的集中力 F 值与跨中挠度δ的关系曲线图,纵向 坐标为力 F(kN),横坐标为跨中挠度 w (mm)。由图 3-10 可见到,当荷载较小时,挠度随 着力 F 的增加而不断增长,两者基本上成比例;当 F≈4.4kN 时,梁 CD 段的下部观察到竖 向裂缝,此后挠度就比力 F 增加得快,并出现了若干条新裂缝;当 F≈14.8kN 时,裂缝急 剧开展,挠度急剧增大;当 F≈15.3kN 时,试验梁截面受压区边缘混凝土被压碎,梁不能 继续负担力 F 值而破坏。 纵向钢筋屈服 裂缝即将出现 破坏 ( ) ( ) Ⅰ Ⅱ Ⅲ Ⅰ Ⅱ Ⅲ 图 3-10 试验梁的荷载-挠度(F-w )图 由图 3-10 还可以看到,试验梁的 F- w 曲线上有两个明显的转折点,从而把梁的受力 和变形全过程分为三个阶段。这三个阶段是:第 I 阶段,梁没有裂缝;第 II 阶段,梁带有 裂缝工作;第 III 阶段,裂缝急剧开展,纵向受力钢筋应力维持在屈服强度不变。同时试验 梁的 F-w 曲线上有三个特征点,即第 I 阶段末(用 Ia表示),裂缝即将出现;第 II 阶段末 (用 IIa表示),纵向受力钢筋屈服;第 III 阶段末(用 IIIa表示),梁受压区混凝土被压碎, 整个梁截面破坏。 2)梁正截面上的混凝土应力分布规律 图3-11为试验梁在各级荷载下截面的混凝土应变实测的平均值及相应于各工作阶段截 面上正应力分布图。 由[图 3-11a)]可见,随着荷载的增加,应变值也不断增加,但应变图基本上仍是上 下两个对顶的三角形。同时还可以看到,随着荷载的增加,中和轴逐渐上升。 在试验中,通过应变仪可以直接测得混凝土的应变和钢筋的应变,要得到截面上的应 力必须从材料的应力-应变关系去推求。图 3-12 为试验梁的混凝土和钢筋试件得到的应力- 应变曲线。图 3-11b)的应力图是根据图 3-11a)的各测点(a、b、c、d、e 测点)的实测 应变值以及图 3-12 中材料的应力-应变图,沿截面从上到下,一个测点一个测点地推求出 来的
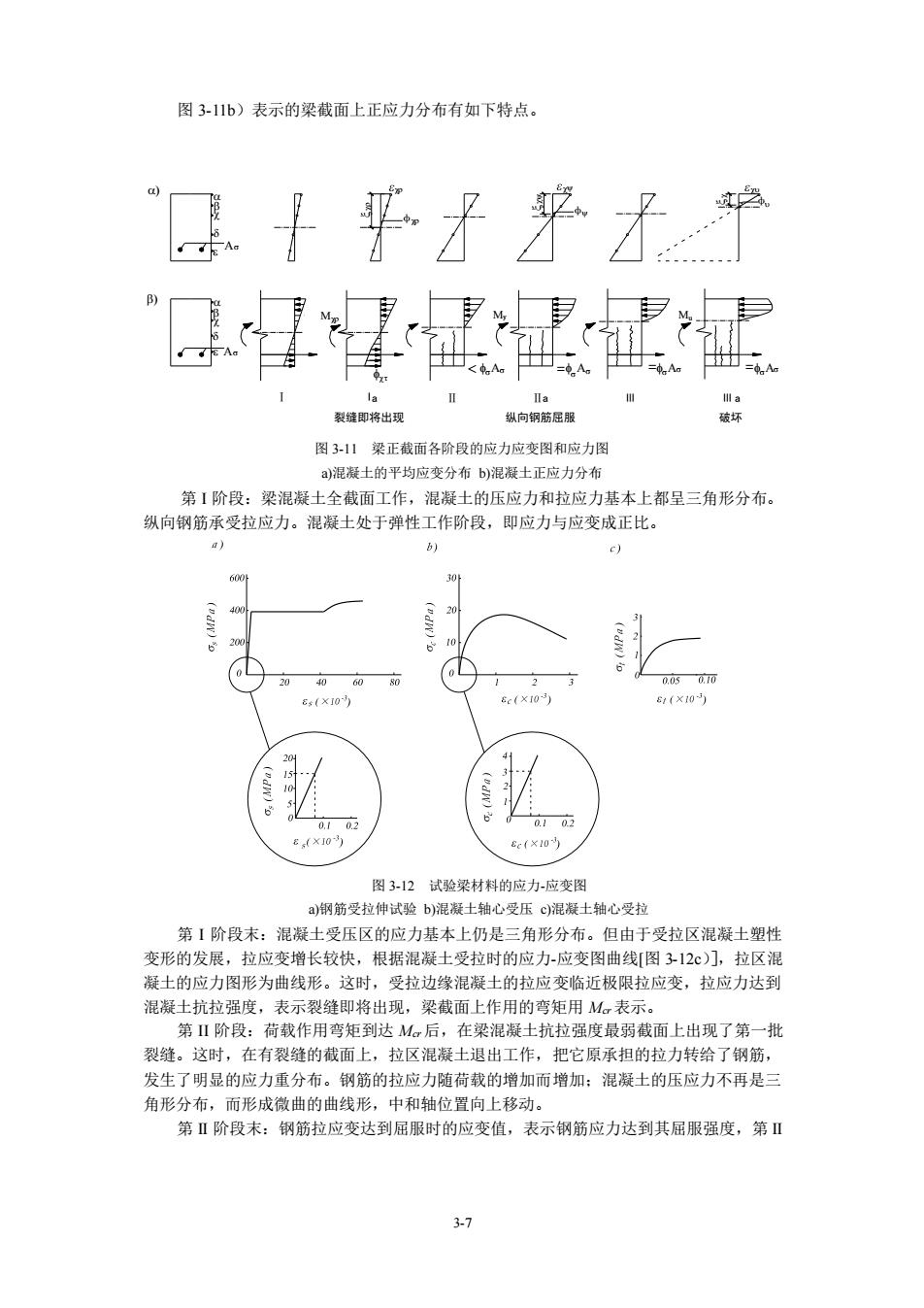
图31b)表示的梁截面上正应力分布有如下特点。 口平界来才 A 装即出 图3-11梁正截而各阶段的应力应变图和应力图 混凝士的平均应变分布)混凝士正应力分 第I阶段:梁混凝土全截面工作,混凝土的压应力和拉应力基本上都呈三角形分布。 纵向钢筋承受拉应力。混凝士处于弹性工作阶段,即应力与应变成正比。 0 1应 6×10 图312试验梁材料的应力-应变图 )钢筋受拉仲试验b)混凝土轴心受压©)混凝土轴心受拉 第I阶段末:混凝土受压区的应力基本上仍是三角形分布。但由于受拉区混凝土塑性 变形的发展,拉应变增长较快,根据混凝土受拉时的应力-应变图曲线图312)门,拉区混 凝士的应力图形为曲线形。这时,受拉边缘混凝土的拉应变临近极限拉应变,拉应力达到 混凝土抗拉强度,表示裂缝即将出现,梁截面上作用的弯矩用M从。表示 第Ⅱ阶段:荷载作用弯矩到达M。后,在梁混凝士抗拉强度最弱截面上出现了第一批 裂缝。这时,在有裂缝的截面上,拉区混凝土退出工作,把它原承担的拉力转给了钢筋, 发生了明显的应力重分布。钢筋的拉应力随荷载的增加而增加:混凝土的压应力不再是三 角形分布,而形成微曲的曲线形,中和轴位置向上移动。 第Ⅱ阶段末:钢筋拉应变达到屈服时的应变值,表示钢筋应力达到其屈服强度,第Ⅱ
3-7 图 3-11b)表示的梁截面上正应力分布有如下特点。 φ φ φ = y = u Ⅰ Ⅰa Ⅱ Ⅱa Ⅲ Ⅲa 裂缝即将出现 纵向钢筋屈服 ) ) = 破坏 图 3-11 梁正截面各阶段的应力应变图和应力图 a)混凝土的平均应变分布 b)混凝土正应力分布 第 I 阶段:梁混凝土全截面工作,混凝土的压应力和拉应力基本上都呈三角形分布。 纵向钢筋承受拉应力。混凝土处于弹性工作阶段,即应力与应变成正比。 图 3-12 试验梁材料的应力-应变图 a)钢筋受拉伸试验 b)混凝土轴心受压 c)混凝土轴心受拉 第 I 阶段末:混凝土受压区的应力基本上仍是三角形分布。但由于受拉区混凝土塑性 变形的发展,拉应变增长较快,根据混凝土受拉时的应力-应变图曲线[图 3-12c)],拉区混 凝土的应力图形为曲线形。这时,受拉边缘混凝土的拉应变临近极限拉应变,拉应力达到 混凝土抗拉强度,表示裂缝即将出现,梁截面上作用的弯矩用 Mcr 表示。 第 II 阶段:荷载作用弯矩到达 Mcr 后,在梁混凝土抗拉强度最弱截面上出现了第一批 裂缝。这时,在有裂缝的截面上,拉区混凝土退出工作,把它原承担的拉力转给了钢筋, 发生了明显的应力重分布。钢筋的拉应力随荷载的增加而增加;混凝土的压应力不再是三 角形分布,而形成微曲的曲线形,中和轴位置向上移动。 第 II 阶段末:钢筋拉应变达到屈服时的应变值,表示钢筋应力达到其屈服强度,第 II

阶段结束。 第Ⅲ阶段:在这个阶段里,钢筋的拉应变增加很快,但钢筋的拉应力一般仍维持在屈 服品度不变(对具右明显流幅的飘筋)。这时,裂锋急剧开展,中和轴珠续上升,混凝土受 压区不断缩小,压应力也不断增大,压应力图成为明显的丰满曲线形。 第Ⅲ阶段末:这时,截面受压上边缘的混凝土压应变达到其极限压应变值,压应力图 呈明显曲线形,并且最大压应力己不在上边缘而是在距上边缘稍下处,这都是混凝士受压 时的应力-应变图所决定的。在第Ⅲ阶段末,压区混凝土的抗压强度耗尽,在临界裂缝两 侧的一定区段内,压区混凝土出现纵向水平裂缝,随即混凝土被压碎、梁玻坏,在这个阶 段,向钢筋的拉应力仍维持在屈服强度。 以上是适量配筋情况下的钢筋混凝土梁从加荷开始至破坏的全过程。由上述可见,出 钢筋和混凝土两种材料组成的钢筋混凝土梁,是不同于连续、匀质、弹性材料梁的,其受 力特点为: (1)钢筋混凝士土梁的截面正应力状态随者荷载的增大不仅有数量上的变化,而且有性 质上的改变一一应力分布图形改变。不同的受力阶段,中和轴的位置及内力偶臂也有所不 短成花论压区混凝土的应力或是纵向受拉钢筋的应九,不像弹性匀质材 (2)梁的大部分工作阶段中,受拉区混凝土己开裂。随着裂缝的开展,压区混凝士塑 性变形也不完全服从弹性匀质梁所具有的比例关系。 上述特点反映了混凝士结构的材料力学性能两个基本方面,即混凝土的抗拉强度比抗 压强度小很多,在不大的拉伸变形下即出现裂缝:混凝士是弹塑性材料,当应力超过一定 限度时,将出现塑性变形 3.2.2受弯构件正截面破坏形态 钢筋混凝土受弯构件有两种破坏性质:一种是塑性破坏(延性破坏),指的是结构或构 件在破坏前有明显变形或其他征兆:另一种是脆性破坏,指的是结构或构件在破坏前无明 显变形或其他征兆。根据试验研究,钢筋混凝土受弯构件 破坏性质与配筋率p、钢筋 度等 、混凝土强度 等级有关。对常用的热 钢筋和普通强度混凝士 波坏形态主要受 配筋率ρ的影响。因此,按照钢筋混凝土受弯构件的配筋情况及相应发生破坏时的性质可 得到正截面破坏的三种形态。 1)适筋梁破坏 一塑性破坏图3-13a)】 梁的受拉区钢筋首先达到屈服强度,其应力保持不变而应变显著地增大,直到受压区 边缘混凝土的应变达到极限压应变时,受压区出现纵向水平裂缝随之混凝土压碎而破坏 这种梁破坏前,梁的裂缝急剧开展,挠度较大,梁截面产生较大的塑性变形,因而有明显 的破坏预兆,属于塑性破坏。图3-9所示钢筋混凝土试验梁的破坏就属适筋梁破坏。 受弯构件的截面曲率·是一项综合表达构件的刚度、变形能力的指标。钢筋混凝土柔 载面曲率的表达式是中=。(图31),其中:为截面边缘混凝土应变:加为战面有效 S,ho 高度:5为相对受压区高度,而受压区高度x=5,。图311中,,为钢筋屈服时截面曲 率,为梁破坏时的极限曲率,由于的急剧增大,,伽的迅速变小,使得比中,大得
3-8 阶段结束。 第 III 阶段:在这个阶段里,钢筋的拉应变增加很快,但钢筋的拉应力一般仍维持在屈 服强度不变(对具有明显流幅的钢筋)。这时,裂缝急剧开展,中和轴继续上升,混凝土受 压区不断缩小,压应力也不断增大,压应力图成为明显的丰满曲线形。 第 III 阶段末:这时,截面受压上边缘的混凝土压应变达到其极限压应变值,压应力图 呈明显曲线形,并且最大压应力已不在上边缘而是在距上边缘稍下处,这都是混凝土受压 时的应力-应变图所决定的。在第 III 阶段末,压区混凝土的抗压强度耗尽,在临界裂缝两 侧的一定区段内,压区混凝土出现纵向水平裂缝,随即混凝土被压碎、梁破坏,在这个阶 段,向钢筋的拉应力仍维持在屈服强度。 以上是适量配筋情况下的钢筋混凝土梁从加荷开始至破坏的全过程。由上述可见,由 钢筋和混凝土两种材料组成的钢筋混凝土梁,是不同于连续、匀质、弹性材料梁的,其受 力特点为: (1)钢筋混凝土梁的截面正应力状态随着荷载的增大不仅有数量上的变化,而且有性 质上的改变——应力分布图形改变。不同的受力阶段,中和轴的位置及内力偶臂也有所不 同的。因此,无论压区混凝土的应力或是纵向受拉钢筋的应力,不像弹性匀质材料梁那样 完全与弯矩成比例。 (2)梁的大部分工作阶段中,受拉区混凝土已开裂。随着裂缝的开展,压区混凝土塑 性变形也不完全服从弹性匀质梁所具有的比例关系。 上述特点反映了混凝土结构的材料力学性能两个基本方面,即混凝土的抗拉强度比抗 压强度小很多,在不大的拉伸变形下即出现裂缝;混凝土是弹塑性材料,当应力超过一定 限度时,将出现塑性变形。 3.2.2 受弯构件正截面破坏形态 钢筋混凝土受弯构件有两种破坏性质:一种是塑性破坏(延性破坏),指的是结构或构 件在破坏前有明显变形或其他征兆;另一种是脆性破坏,指的是结构或构件在破坏前无明 显变形或其他征兆。根据试验研究,钢筋混凝土受弯构件的破坏性质与配筋率ρ、钢筋强 度等级、混凝土强度等级有关。对常用的热轧钢筋和普通强度混凝土,破坏形态主要受到 配筋率ρ的影响。因此,按照钢筋混凝土受弯构件的配筋情况及相应发生破坏时的性质可 得到正截面破坏的三种形态。 1)适筋梁破坏——塑性破坏[图 3-13a)] 梁的受拉区钢筋首先达到屈服强度,其应力保持不变而应变显著地增大,直到受压区 边缘混凝土的应变达到极限压应变时,受压区出现纵向水平裂缝随之混凝土压碎而破坏。 这种梁破坏前,梁的裂缝急剧开展,挠度较大,梁截面产生较大的塑性变形,因而有明显 的破坏预兆,属于塑性破坏。图 3-9 所示钢筋混凝土试验梁的破坏就属适筋梁破坏。 受弯构件的截面曲率 是一项综合表达构件的刚度、变形能力的指标。钢筋混凝土梁 截面曲率的表达式是 ih0 c = (图 3-11),其中εc为截面边缘混凝土应变;h0 为截面有效 高度; i 为相对受压区高度,而受压区高度 xi= i h0。图 3-11 中, y 为钢筋屈服时截面曲 率, u 为梁破坏时的极限曲率,由于εc的急剧增大, i h0 的迅速变小,使得 u 比 y 大得

很多,即(中~中,)较大,说明构件刚度降低、变形增大,但却表现了较好的耐受变形的 能力一一延性。延性是承受地震及冲击荷载作用时构件的一项重要受力特性。 图313桑的破坏形态 )适筋梁破坏b)超筋梁破坏9少筋梁破坏 2)超筋梁破坏 一脆性破坏图3-13b)】 当梁裁面配筋率ρ增大,钢筋应力增加缓慢,压区混凝土应力有较快的增长,P越大 则纵向钢筋屈服时的弯矩M越趋近梁破坏时的弯矩M,这意味着第Ⅲ阶段缩短。当P增 大到使=(时,受拉钢筋屈服与压风混凝土压碎几平同时发生,这种破坏称为平衡破坏 或界限破坏,相应的p值被称为最大配筋率m 当士际配流率 时,梁的破坏时压风湿被压坏而母拉银流应力尚未法 到屈服强度。破坏前梁的挠度及截面曲率曲线没有明显的转折点(图3-14),受拉区的裂 开展不宽,延伸不高,破坏是突然的,没有明显预兆,属于脆性破坏,称为超筋梁破坏。 、一破环(超防梁) 一破环(适筋梁 2 >开袋 20 @(μμ) 图3.14三种破坏特征梁的一挡府曲线 超筋梁的破坏是压区混凝士抗压强度耗尽,而钢筋的抗拉强度没有得到充分发挥,因 g
3-9 很多,即( u - y )较大,说明构件刚度降低、变形增大,但却表现了较好的耐受变形的 能力——延性。延性是承受地震及冲击荷载作用时构件的一项重要受力特性。 图 3-13 梁的破坏形态 a)适筋梁破坏 b)超筋梁破坏 c)少筋梁破坏 2)超筋梁破坏——脆性破坏[图 3-13b)] 当梁截面配筋率ρ增大,钢筋应力增加缓慢,压区混凝土应力有较快的增长,ρ越大, 则纵向钢筋屈服时的弯矩 My越趋近梁破坏时的弯矩 Mu,这意味着第 III 阶段缩短。当ρ增 大到使 My=Mu 时,受拉钢筋屈服与压区混凝土压碎几乎同时发生,这种破坏称为平衡破坏 或界限破坏,相应的ρ值被称为最大配筋率ρmax。 当实际配筋率ρ>ρmax 时,梁的破坏时压区混凝土被压坏,而受拉区钢筋应力尚未达 到屈服强度。破坏前梁的挠度及截面曲率曲线没有明显的转折点(图 3-14),受拉区的裂缝 开展不宽,延伸不高,破坏是突然的,没有明显预兆,属于脆性破坏,称为超筋梁破坏。 破坏(超筋梁) 破坏(适筋梁) 纵向钢筋屈服 ( ) ( ) 开裂 破坏(少筋梁) 图 3-14 三种破坏特征梁的荷载-挠度曲线 超筋梁的破坏是压区混凝土抗压强度耗尽,而钢筋的抗拉强度没有得到充分发挥,因

此,超筋梁的破坏时的弯矩M与钢筋强度无关,仅取决于混凝士的抗压强度。 3)少筋梁破坏—脆性破坏图3-13c)】 当梁的配筋率·很少,梁受拉区混凝土开裂后,钢筋应力趋近于屈服强度,即开裂弯 矩M,趋近于受拉区钢筋屈服时的弯矩M,这意味着第Ⅱ阶段的缩短,当P减少到使M一M 时,裂缝一且出现,钢筋应力立即达到屈服强度,这时的配筋率称为最小配筋率Pm· 梁中实际配筋率p小于Pm时,梁受拉区混凝土一开裂,受拉纲筋到达屈服,并迅速 经历整个流幅而进入强化阶段,梁仅出现一条集中裂缝,不仅宽度较大,而且沿梁高延伸 很高,此时受压区混凝土还未压坏,而裂缝宽度己很宽,挠度过大,钢筋甚至被拉新。由 于破坏很突然,故属于胞性破坏。把具有这种破坏形态的梁称为少筋梁 少筋梁的抗弯承载力取决于混凝土的抗拉强度,在桥梁工程中不允许采用。 3.3受弯构件正截面承载力计算的基本原则 3.3.1甚本假定 钢筋混凝土受弯构件达到抗弯承载能力极限状态,其正截面承载力计算采用下述基本 假 1)平截面假定 国内外大量试验证明,对于钢筋混凝土受弯物件,从开始加荷直至时坏的名阶段,浅 受压区来讲,平截面假定是1 受拉区 在裂缝产生后,裂缝截面处钢筋和相邻的混凝士之 发生了 对滑移,因而,在裂缝附近区段,截面变形已不能完全符合平截面假定。然而。如果量测 应变的标距较长(跨过一条或几条裂缝),则其平均应变还是能较好地符合平截面假定的。 试哈还表明,构件破坏时,受压风混凝土的压碎是在沿物件长度一定范围内发生的,同时 受拉钢筋的屈服也是在一定长度范围内发生的,因此, 在承载力计算时采用平截面假定是 可行 当然,这一假定是近似的,它与实际情况或多或少存在某些差距,但是,分析表明, 由此而引起的误差是不大的,完全能符合工程计算要求。 平截面假定为钢筋混凝土受弯构件正截面承载力计算提供了变形协调的几何关系,可 加强计算方法的逻辑性和条理性,使计算公式具有更明确的物理意义,因此,世界上许多 国家的设计规范都采用了 一假定。 2)不考虑混凝土的抗拉强度 在裂缝截面处,受拉区混凝士已大部分退出工作,但在靠近中和轴附近,仍有一部分 混凝土承担着拉应力。由于其拉应力较小,且内力偶臂也不大,因此,所承担的内力矩是 不大的,故在计算中可忽略不计。 3)材料应力应变物理关系 (1)混凝土受压时的应力应变关系。关于混凝土的应力应变曲线,有多种不同的计算 图式,较常用的是由一条一次抛物线及水平线组成的曲线。图315是歌洲湿凝土协会的标 准规范(CEB-FIP Mode Code)采用作为计算的典型化混凝土应力应变曲线。曲线的上升段 OA为二次抛物线,其表达式为 3-10
3-10 此,超筋梁的破坏时的弯矩 Mu 与钢筋强度无关,仅取决于混凝土的抗压强度。 3)少筋梁破坏——脆性破坏[图 3-13c)] 当梁的配筋率ρ很少,梁受拉区混凝土开裂后,钢筋应力趋近于屈服强度,即开裂弯 矩Mcr 趋近于受拉区钢筋屈服时的弯矩My,这意味着第II 阶段的缩短,当ρ减少到使Mcr=My 时,裂缝一旦出现,钢筋应力立即达到屈服强度,这时的配筋率称为最小配筋率ρmin。 梁中实际配筋率ρ小于ρmin 时,梁受拉区混凝土一开裂,受拉钢筋到达屈服,并迅速 经历整个流幅而进入强化阶段,梁仅出现一条集中裂缝,不仅宽度较大,而且沿梁高延伸 很高,此时受压区混凝土还未压坏,而裂缝宽度已很宽,挠度过大,钢筋甚至被拉断。由 于破坏很突然,故属于脆性破坏。把具有这种破坏形态的梁称为少筋梁。 少筋梁的抗弯承载力取决于混凝土的抗拉强度,在桥梁工程中不允许采用。 3.3 受弯构件正截面承载力计算的基本原则 3.3.1 基本假定 钢筋混凝土受弯构件达到抗弯承载能力极限状态,其正截面承载力计算采用下述基本 假定: 1)平截面假定 国内外大量试验证明,对于钢筋混凝土受弯构件,从开始加荷直至破坏的各阶段,截 面的平均应变都能较好地符合平截面假定。对混凝土受压区来讲,平截面假定是正确的。 而对于混凝土受拉区,在裂缝产生后,裂缝截面处钢筋和相邻的混凝土之间发生了某些相 对滑移,因而,在裂缝附近区段,截面变形已不能完全符合平截面假定。然而。如果量测 应变的标距较长(跨过一条或几条裂缝),则其平均应变还是能较好地符合平截面假定的。 试验还表明,构件破坏时,受压区混凝土的压碎是在沿构件长度一定范围内发生的,同时, 受拉钢筋的屈服也是在一定长度范围内发生的,因此,在承载力计算时采用平截面假定是 可行的。 当然,这一假定是近似的,它与实际情况或多或少存在某些差距,但是,分析表明, 由此而引起的误差是不大的,完全能符合工程计算要求。 平截面假定为钢筋混凝土受弯构件正截面承载力计算提供了变形协调的几何关系,可 加强计算方法的逻辑性和条理性,使计算公式具有更明确的物理意义,因此,世界上许多 国家的设计规范都采用了这一假定。 2)不考虑混凝土的抗拉强度 在裂缝截面处,受拉区混凝土已大部分退出工作,但在靠近中和轴附近,仍有一部分 混凝土承担着拉应力。由于其拉应力较小,且内力偶臂也不大,因此,所承担的内力矩是 不大的,故在计算中可忽略不计。 3)材料应力应变物理关系 (1)混凝土受压时的应力应变关系。关于混凝土的应力应变曲线,有多种不同的计算 图式,较常用的是由一条二次抛物线及水平线组成的曲线。图 3-15 是欧洲混凝土协会的标 准规范(CEB-FIP Mode Code)采用作为计算的典型化混凝土应力应变曲线。曲线的上升段 OA 为二次抛物线,其表达式为