
实际应用注意: >上述用经典力学的方法来处理分子的振动是为了得 到宏观的图像,便于理解并有一定性概念。但二个 真实的微观粒子需要用量子理论方法加以理解,如 能量量子化。 >实际上,在一个分子中,基团与基团间,基团中的 化学键之间都相互有影响,因此基本振动频率除了 决定于化学键两端的原子质量、化学键的力常数外, 还与内部因素(结构因素)及外部因素(化学环境) 有关
实际应用注意: ➢ 上述用经典力学的方法来处理分子的振动是为了得 到宏观的图像,便于理解并有一定性概念。但一个 真实的微观粒子需要用量子理论方法加以理解,如 能量量子化。 ➢ 实际上,在一个分子中,基团与基团间,基团中的 化学键之间都相互有影响,因此基本振动频率除了 决定于化学键两端的原子质量、化学键的力常数外, 还与内部因素(结构因素)及外部因素(化学环境) 有关

§10-4分子振动的形式(多原子分子) 双原子分子振动简单,而多原子分子中情况变 得复杂,但可以把其振动分解为许多简单的基 本振动。 >以亚甲基为例,分子的振动形式可分为两类: 伸缩振动和变形或弯曲振动。 伸缩振动 指键长沿建轴方向发生周期性变化的振动。 变形振动(弯曲振动,变角振动)一一 指键角发生周期性变化、而键长不变的振动
➢ 双原子分子振动简单,而多原子分子中情况变 得复杂,但可以把其振动分解为许多简单的基 本振动。 ➢ 以亚甲基为例,分子的振动形式可分为两类: 伸缩振动和变形或弯曲振动。 伸缩振动—— 指键长沿键轴方向发生周期性变化的振动。 变形振动(弯曲振动,变角振动)—— 指键角发生周期性变化、而键长不变的振动 §10-4 分子振动的形式(多原子分子)

1。两类基本振动形式 伸缩振动 (亚甲基) 对称伸缩振动反对称伸缩振动 Us:2926 cm-1 Uas 2853 cm- (强吸收S) 变形振动 (亚甲基): 摇摆(面外)扭曲 剪式(面内)摇摆 v:1306-1303cm1T:1250cm1δ:1468cm1p:720cm1 (弱吸收四) (中等吸收) 00:57:06
00:57:06 1.两类基本振动形式 变形振动 (亚甲基): 伸缩振动 (亚甲基):

2。振动的自由度 指分子的基本振动数目。 >N个原子组成分子,每个原子在空间具三个自由度 分子自由度=3N=平动自由度+转动自由度+振动自由度 分子振动自由度=3N-(平动自由度+转动自由度) 非线性分子:F=3V-6 线性分子:F=3W-5 注: 对于红外吸收来说,振动自由度反映吸收峰数量 但吸收峰数与振动自由度数往往不符(吸收峰数常 少于振动数目)
✓ 注: 对于红外吸收来说,振动自由度反映吸收峰数量, 但吸收峰数与振动自由度数往往不符(吸收峰数常 少于振动数目)。 2.振动的自由度 指分子的基本振动数目。 ➢ N个原子组成分子,每个原子在空间具三个自由度 分子自由度 = 3N = 平动自由度+转动自由度+振动自由度 分子振动自由度 = 3N −(平动自由度+转动自由度) 非线性分子:F = 3N − 6 线性分子:F = 3N −5
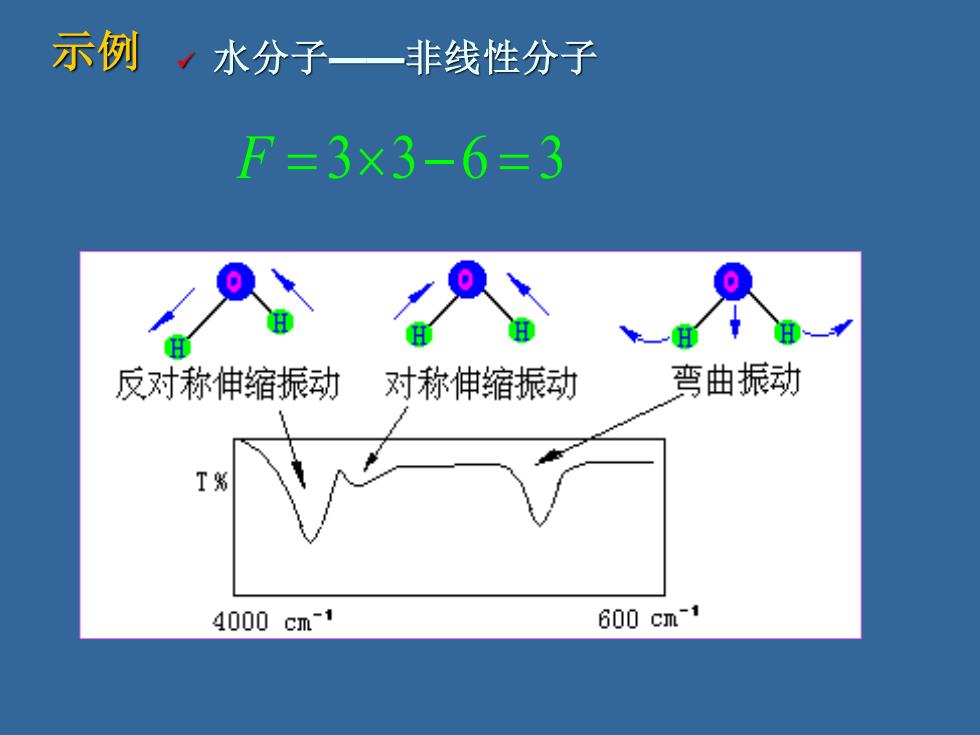
示例,水分子一非线性分子 F=3×3-6=3 H 反对称伸缩振动 对称伸缩振动 弯曲振动 T% 4000cm-1 600cm-1
示例 ✓ 水分子——非线性分子 F = 33−6 = 3