§10一2红外吸收光谱的产生条件 满足两个条件: ()辐射应具有刚好能满足物质跃迁时所需的能量; (2)辐射与物质之间有偶合作用(相互作用) 对称分子:没有偶极矩,辐 射不能引起共振,无红外活性。 作用力 如:N2、O2、CL2等。 偶极 电场 非对称分子:有偶极矩, 红 外活性。 d HC1 H20 q 相当于:偶极子在交变电场 (电 +q -q +g +q 磁辐射的电场)中作用,示意图)
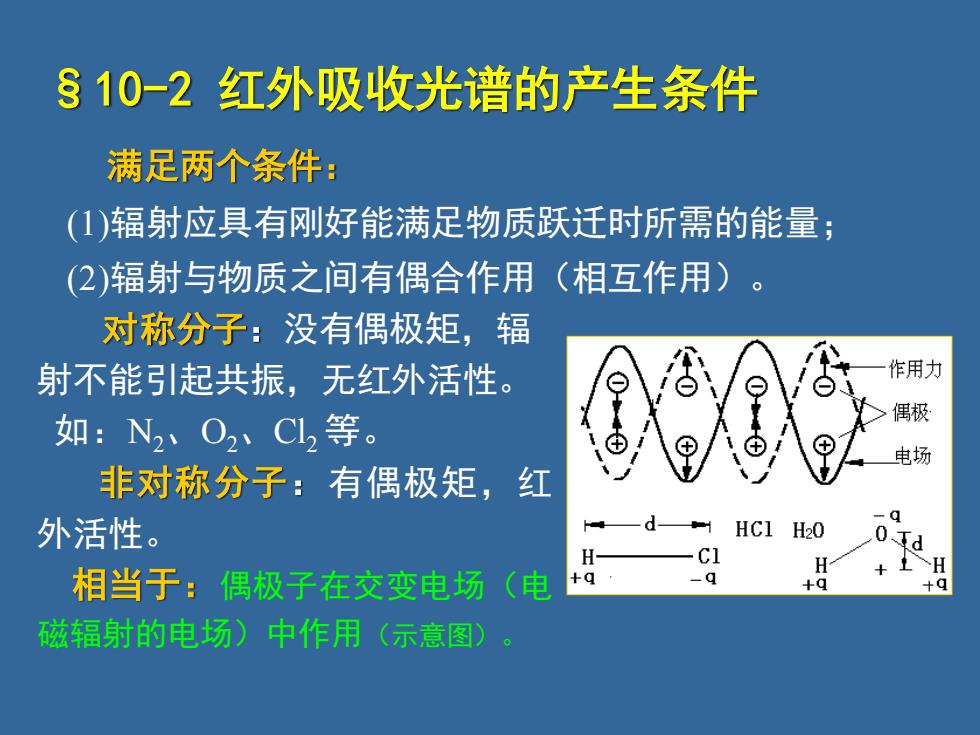
§10-2 红外吸收光谱的产生条件 满足两个条件: (1)辐射应具有刚好能满足物质跃迁时所需的能量; (2)辐射与物质之间有偶合作用(相互作用)。 对称分子:没有偶极矩,辐 射不能引起共振,无红外活性。 如:N2、O2、Cl2 等。 非对称分子:有偶极矩,红 外活性。 相当于:偶极子在交变电场(电 磁辐射的电场)中作用(示意图)

红外吸收光谱图:用连续改变频率的红外光照射试样得到。 当一定频率的红外光照射分子时,如果分子中某 个基团的振动频率和它一样,二者就会产生共振,此 时光的能量通过分子偶极矩的变化而传递给分子,这 个基团就吸收一定频率的红外光,产生振动跃迁;如 果红外光的振动频率和分子中各基团的振动频率不符 合,该部分的红外光就不会吸收。 4000 3000.2500 2400 150013W 11(010090 800 70 650 100 80 40 d 1680( 2.5 1011 12 13 16
当一定频率的红外光照射分子时,如果分子中某 个基团的振动频率和它一样,二者就会产生共振,此 时光的能量通过分子偶极矩的变化而传递给分子,这 个基团就吸收一定频率的红外光,产生振动跃迁;如 果红外光的振动频率和分子中各基团的振动频率不符 合,该部分的红外光就不会吸收。 红外吸收光谱图:用连续改变频率的红外光照射试样得到

§10-3分子振动方程 1.分子振动模型 多原子分子→双原子集合 双原子分子A-B→ 近似看作谐振子 两原子间的伸缩振动 6wO 一→近似看作简谐振动 伸 缩 伸 该体系的振动频率可 由虎克定律得到: 平衡位置 平衡位置 130 谐振子振动示意图 2πC
§10-3 分子振动方程 双原子分子A-B→ 近似看作谐振子 两原子间的伸缩振动 →近似看作简谐振动 该体系的振动频率可 由虎克定律得到: 1. 分子振动模型 多原子分子→ 双原子集合 k k c 1307 2 1 1 = = =

0= =1307 k: 化学键的力常数,与键能和键长有关; 4:双原子的折合质量4=m2/(m1十) 因此,影响基本振动频率的直接因素是相对原子质量 和化学键的力常数,即取决于分子的结构特征。 化学键键强越强(即键的力常数越大)原子折合质量越小, 化学键的振动频率越大,吸收峰将出现在高波数区。 键类型 -C≡C一>-C=C一>-C一C 力常数 15~17 9.5×9.9 4.55.6 峰位 2222cm1 1667 cm1 1428cmr1
k:化学键的力常数,与键能和键长有关; :双原子的折合质量 =m1m2 /(m1+m2) 因此,影响基本振动频率的直接因素是相对原子质量 和化学键的力常数,即取决于分子的结构特征。 k k c 1307 2 1 1 = = = 化学键键强越强(即键的力常数k越大)原子折合质量越小, 化学键的振动频率越大,吸收峰将出现在高波数区。 键类型 —CC — > —C =C — > —C — C — 力常数 15 17 9.5 9.9 4.5 5.6 峰位 2222cm-1 1667 cm-1 1428 cm-1

表 某些键的伸缩力常数 (N.cm-1) 键 分子 k 键 分子 k H-F HF 9.7 H-C CH2-CH2 5.1 H-C1 HC1 4.8 H-C CH≡CH H-Br HBr 4.1 C-Cl CH3Cl H-I HI 3.2 C-C 4.5w5.6 H- H20 7.8 C-c 9.5m9.9 H-S H2S 4.3 C=C 15w17 H-N NH3 6.5 C-0 12~13 H-C CHaX 4.7w5.0 C=0 16m18 例题:由表中查知C=C的=9.5~9.9,令其为9.6, 计算波数值。 =1 =1307 9.6 1307 =1653cm 2πc4 12/2 正己烯中C÷C键伸缩振动频率实测值为1652cm-:
表 某些键的伸缩力常数(N.cm-1) 例题: 由表中查知C=C的k=9.5 9.9 ,令其为9.6, 计算波数值。 1 1653cm 12 / 2 9.6 1307 1307 2π 1 1 − = = = = = k k c 正己烯中C=C键伸缩振动频率实测值为1652 cm-1