“禁止能量”由于布洛赫波受到布喇格反射 A自由电子 1/3 kr= 3π2N k-<<kz和)>>a ≈3n 很多原子的电子波函数 kBZ≥T 3 U=常量,“自由电子” a 注意:典型的金属V>1,因此,k~kBz 价电子数 aBZ边界 k->k3z和入~a k-<~kz和入>~a 布洛赫波的衍射-布喇格散射“能隙” π a 11
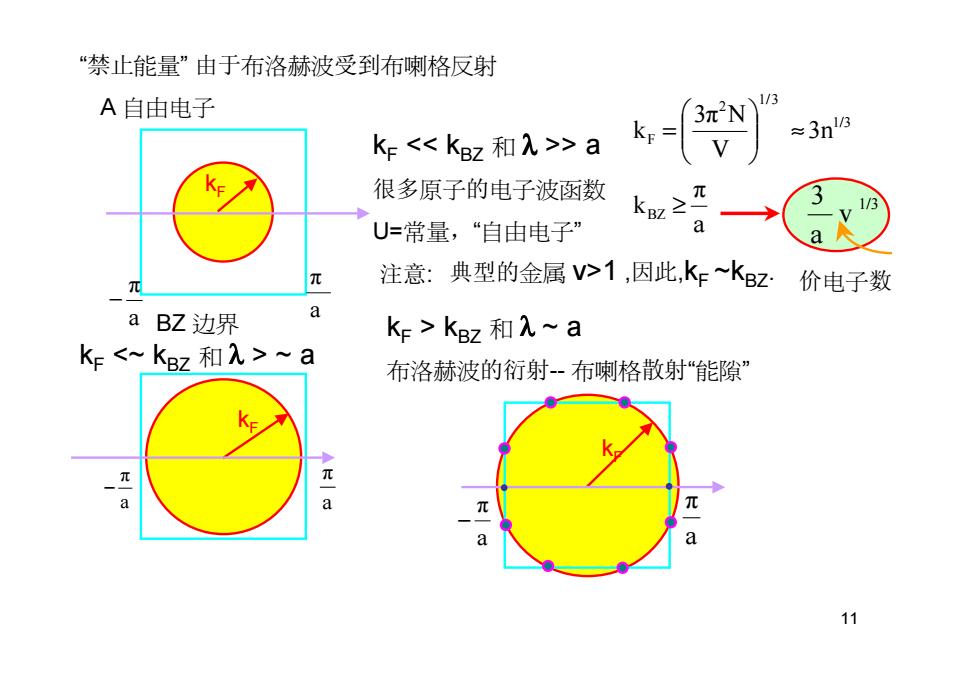
11 “禁止能量” 由于布洛赫波受到布喇格反射 A 自由电子 BZ 边界 kF a π a π − kF << kBZ 和 λ >> a 很多原子的电子波函数 U=常量,“自由电子” aπ k 3n V3π N kBZ 1/3 3/1 2 F ≥ ≈ = 注意: 1/3 v a 3 典型的金属 v>1 ,因此,kF ~kBZ. 价电子数 kF a π kF <~ kBZ 和 λ > ~ a a π − kF a π − aπ kF > kBZ 和 λ ~ a 布洛赫波的衍射- 布喇格散射“能隙

7.2布洛赫波函数 布洛赫定理: k()=uk()exp依·i) 在势能中电子的布洛赫波函数 证明:考虑对称性 W:(x+a)=TWx(x)=cWx(x) 周期性边界条件Vk(X+Na)=TNVk(X)=cNyk(x) =Ψk(X) (1) .cN=1 c的解为: c=exp(i2/Na),s=0,1,2.N-1 只要4(x)=u(x+a),就能满足(I)的关系。 Wr(x)=exp(i2ns/Na)u(x) 布洛赫态不是动量本征态即P≠方k 允许态可以用波矢k标志 能带结构计算给出E(k)它决定动态特性. 12
12 ψ )r( u )r( exp( ki r) k k r r r r 布洛赫定理 : = • 在势能中电子的布洛赫波函数 证明:考虑对称性 周期性边界条件 布洛赫态不是动量本征态 即 P ≠ h k 允许态 可以用波矢 k标志. 能带结构计算 给出 E(k) 它决定动态特性. ψ (x) ψ (x) ˆ ψ (x ) k k k + a = T = c ψ (x) exp( 2 / ) ( ) ( ) ( ), )1( exp( 2 / ), 2,1,0 . 1 1 ψ (x) (1) ψ (x) ψ (x) ˆ ψ (x N ) k N k k N k N k i s Na u x u x u x a c i s Na s N c c a T c k k k π π = 只要 就能满足 的关系。 的解为: ∴ = + = = − ∴ = = + = = 7.2 布洛赫波函数
7.3 Kronig-Penny模型 Kronig-Penny模型 方势阱周期势由Kronig和Penney:提出 U(x) U U(x) a 0在0<x<a U。在-b<x<0 -a-b -b0 aa+b dw(x)U(x)w(x)=e(X) 2m dx2 方势阱U() 0<x<a,W(x)=Aeikx+Be-ikx w/. 方2K2 2m -b<x<0.V@)-Cew+De w.-U-g 边界条件: A+B=C+D (1)x=0 iK(A-B)=q(C-D) 13
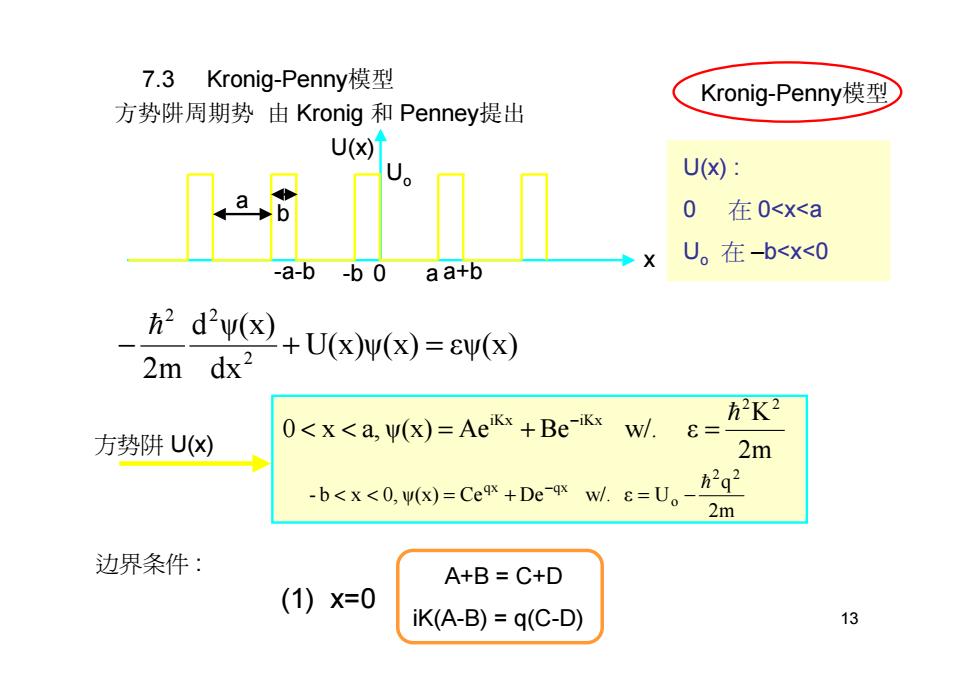
13 方势阱周期势 由 Kronig 和 Penney提出 7.3 Kronig-Penny模型 x -a-b -b 0 a a+b b a U(x) Uo U(x) : 0 在 0<x<a Uo 在 –b<x<0 U(x)ψ(x) εψ(x) dx d ψ(x) 2m 2 2 2 − + = h 方势阱 U(x) A+B = C+D iK(A-B) = q(C-D) (1) x=0 边界条件 : 2m K 0 x a, ψ(x) Ae Be w/. ε 2 2 iKx iKx h < < = + = − 2mq - b x 0, ψ(x) Ce De w/. ε U 2 2 o qx qx h < < = + = − − Kronig-Penny模型

其它边界情况如何呢? x=a? Ψ(a<x<a+b)是什么情况? ×=-b?Ψ(-a-b<x<-b)是什么情况? 由布洛赫定理V(a<x<a+b)=y(-bx<0)eik(a+b) Y(-a-b<x<-b)=W(O<x<a)e-ik(a+b) (2)X=a AeKx+Be-ikx =(Ce-+Deb eik(a+b) iK(Aekx-Be-ikx)=qlCe-4b-De9b)ek(a+b) 解(1)和(2) q2-K2 sh(qb)sin(Ka)+ch(qb)cos(Ka)=cos(ka+kb) 2qK 14
14 由布洛赫定理 ψ(a<x<a+b) = ψ(-b<x<0) eik(a+b) ψ(-a-b<x<-b) = ψ(0<x<a) e-ik(a+b) sh(qb)sin(Ka) ch(qb)cos(Ka) cos(ka kb) 2qK q K 2 2 + = + − (2) x=a ( ) iKx iKx qb qb ik(a b) Ae Be Ce De e − − + + = + ( ) ( ) iKx iKx qb qb ik(a b) iK Ae Be q Ce De e − − + − = − 其它边界情况如何呢 ? x = a? ψ ( a<x<a+b ) 是什么情况? x = -b? ψ ( -a-b<x<-b )是什么情况? 解 (1) 和 (2)

结果可以简化成一个周期性delta势能 b→0和U。→∞ 因此,bU。是有限的且 bU。=be+ 方2bq2 保持有限! 2m 2m q2-K2 q q 和sh(qb)→qb 2gK 2gK 2K q2ba sin(Ka)+cos(Ka)=cos(ka) 2Ka P:势垒高度测量 P=q'ab_(U。-emab 2 ≈limb-0 ma bU sin(Ka) cos(Ka)=cos(ka) Ka P→0意味着Kk自由电子 15
15 P : 势垒高度测量 P→0 意味着 K→k 自由 电子 cos(Ka) cos(ka) Ka sin(Ka) P + = ( ) ≈ − = = →∞ 2 →0 o 2 o 2 ma bU U ε mab 2 q ab P h l h Uo b im sin(Ka) cos(Ka) cos(ka) 2Ka q ba 2 + = 2K q 2qK q 2qK q K 2 2 2 → = − 和 sh(qb) → qb 结果 可以简化成一个 周期性 delta 势能 b → 0 和 Uo → ∞ 因此, bUo 是有限的且 2mbq 2mq bU b ε 2 2 2 2 o h h → = + 保持有限 !