1D电子波函数:晶格常量a的线性链中的电子 原平 rmnnr k小(2>>a) Ψk~eiki 平面波 k=±元/a(BZ) Vk~e&f±ekr 驻波 归一化 布喇格反射 2cos()=2cos X ≈ a i2sin)=12sin ≈ 6
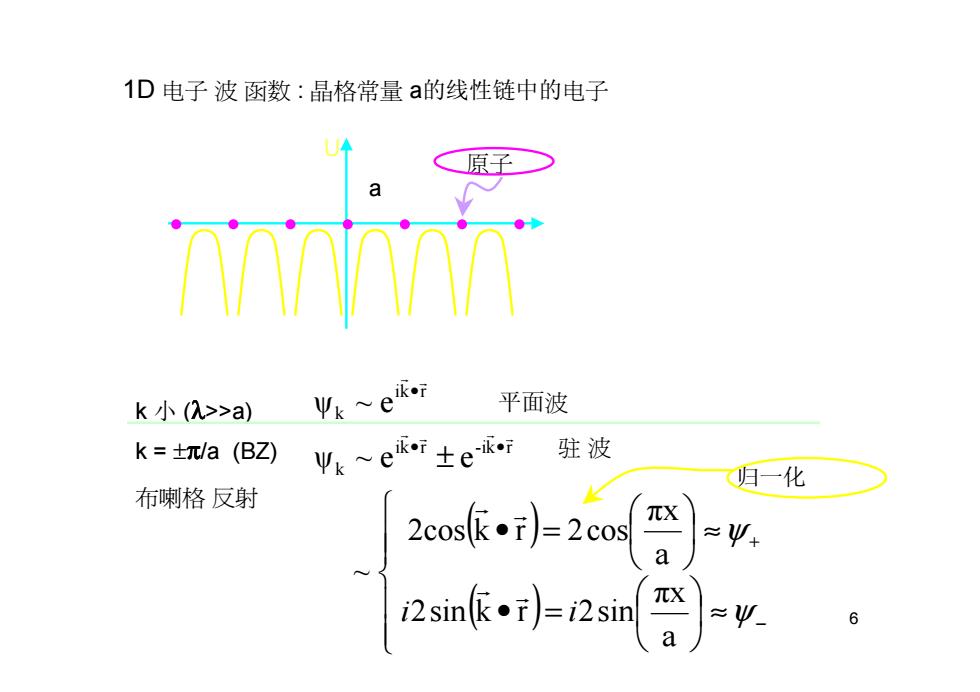
6 1D 电子 波 函数 : 晶格常量 a的线性链中的电子 k 小 (λ>>a) ki r k ψ ~ e r r • k = ±π/a (BZ) ( ) ( ) a πx 2sin k r 2sin a πx 2cos k r 2cos ~ ψ ~ e e ki r -ik r k ≈ • = ≈ • = ± −+ • • ψ ψ i i r r r r r r r r 平面波 驻 波 U x a 原子 布喇格 反射 归一化
电子几率密度 2 元X coS 原子处在高密度 L a 对业+ 2 atom =na 元X sin 对Ψ_ L 原子处在低密度 a w0M0d 来自势能U()的能量 u,-uepf-2jeas U-jw-2jsm 元X a 7
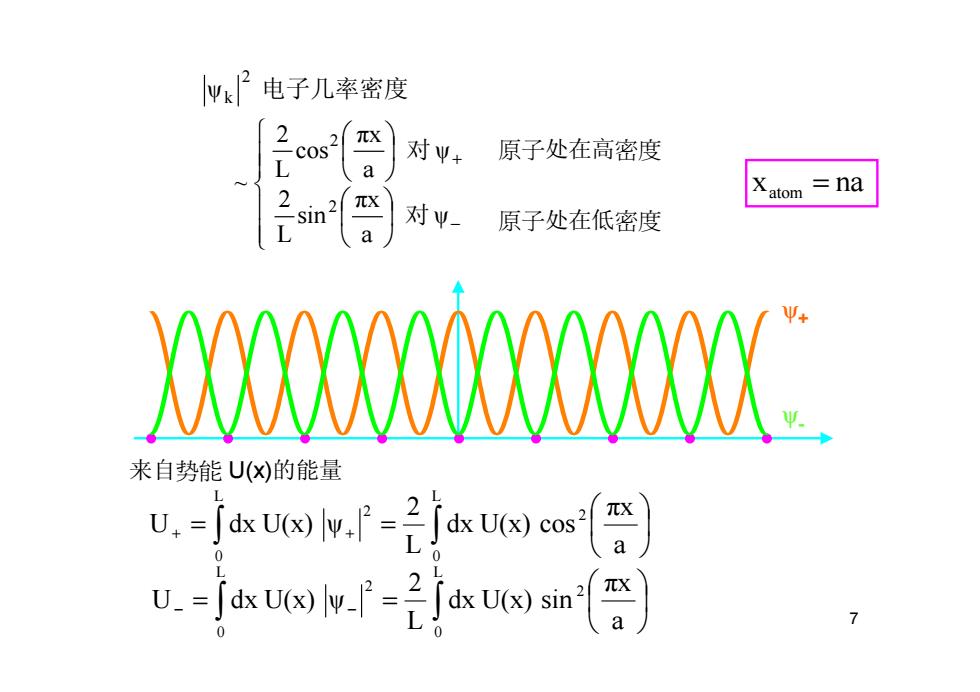
7 ψ a πx sin L 2 ψ a πx cos L 2 ~ ψ 2 2 2 k −+ 对对 电子几率密度 原子处在高密度 原子处在低密度 来自势能 U(x)的能量 a πx dx U(x) sin L2 U dx U(x) ψ a πx dx U(x) cos L2 U dx U(x) ψ L 0 2 L 0 2 L 0 2 L 0 2 ∫ ∫ ∫ ∫ = = = = − − + + 几率 密度 x ψ+ ψ- x na atom =
能量差 -uc oo-in) 2X 自由电子:U=0 Forbidden 能量区 0 BZ 0 结果: 在BZ区边界驻波. 能隙一在此能量,没有波能够穿过晶体 8
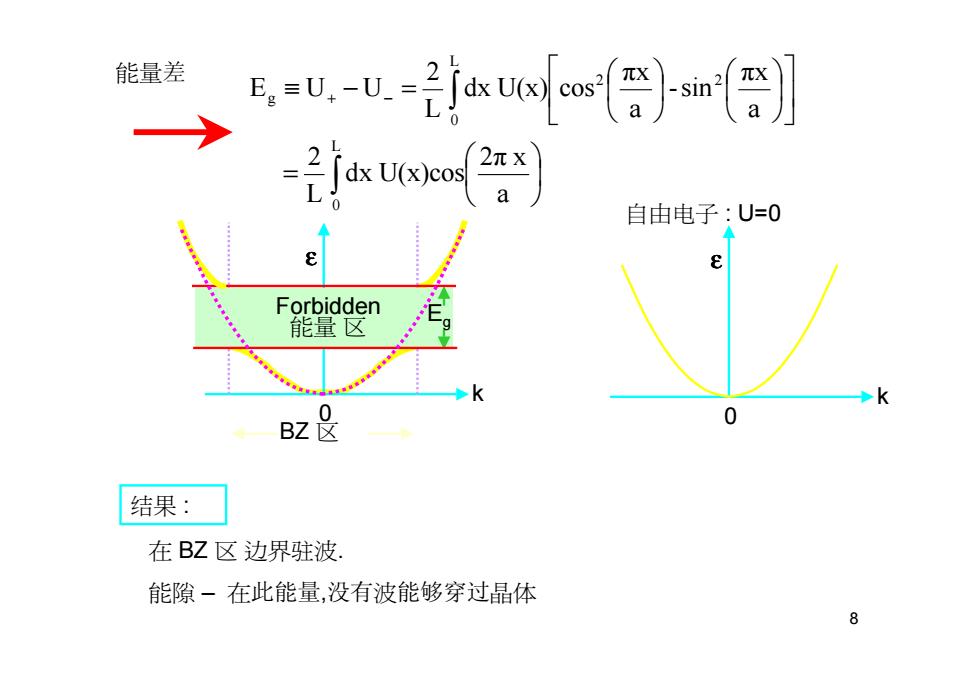
8 a 2π x dx U(x)cos L2 a πx -sin a πx dx U(x) cos L2 E U U L 0 L 0 2 2 g ∫ ∫ = ≡ + − − = 能量差 k ε BZ 区 Eg Forbidden 能量 区 0 自由电子 : U=0 k ε 0 在 BZ 区 边界驻波. 能隙 – 在此能量,没有波能够穿过晶体 结果 :
势能U(x)按傅里叶级数展开:U(X)=(X+a) U(x)=∑U=∑Ua(eos+eor) G G>0 G倒格矢 2π =2∑Uccos(Gx) =nl 其中n为正数 G>0 a 反向变换 dx U(x)cos(Gx) Eg=2U2/a =2 2UG1 能隙等于晶体势能的傅里叶分量· 222222a22828a2a2 例如, U(x)-U,c0s a 之小 U(X) -(v.iL)-v
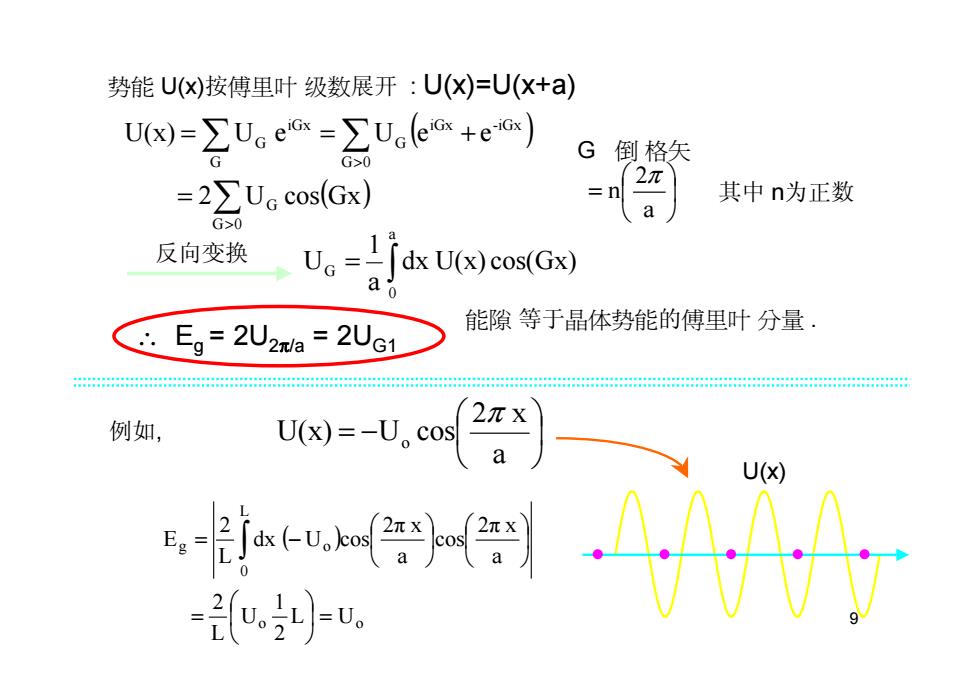
9 ∫ = a 0 G dx U(x) cos(Gx) a 1 反向变换 U ∴ Eg = 2U2π/a = 2UG1 能隙 等于晶体势能的傅里叶 分量 . 例如, ( ) o o L 0 g o L U 2 1 U L 2 a 2π x cos a 2π x dx U cos L 2 E = = = − ∫ x U(x) = − a 2 x U(x) U cos o π 势能 U(x)按傅里叶 级数展开 : U(x)=U(x+a) ( ) ∑ ( ) ∑ ∑ > > = = = + G 0 G G 0 iGx -iGx G G iGx G 2 U cos Gx U(x) U e U e e G : 倒 格矢 其中 n为正数 = a2 n π
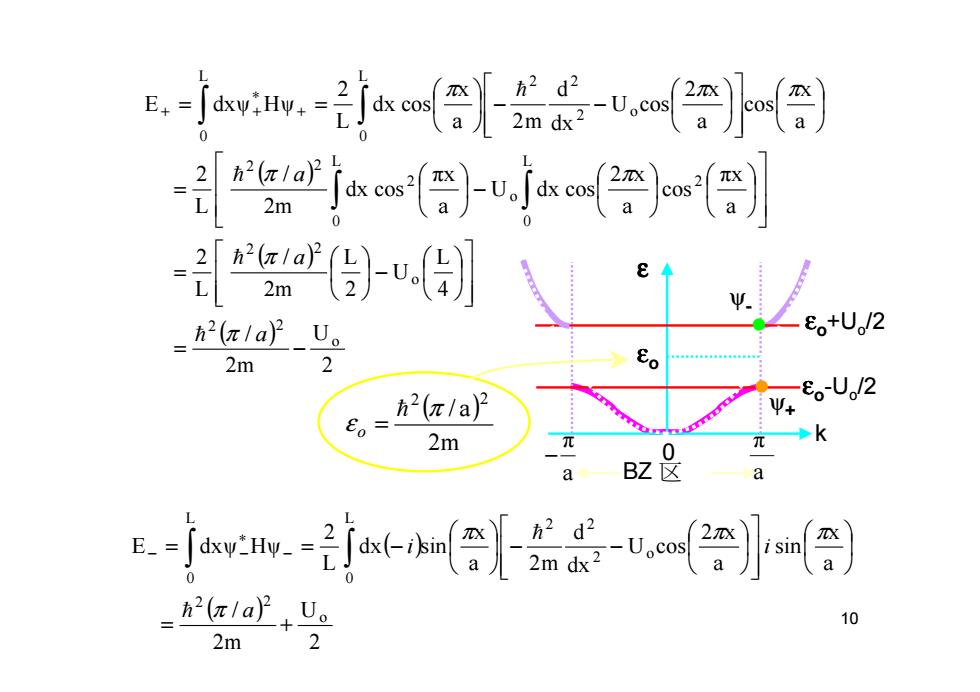
,-jww益-uog) o)-v.a) h2(π1a2U。 Eo+U/2 2m 2 h2(π/a2 。-UJ2 Ψ+ 2m 0 a BZ -jww水-tame( 2πa2+U 10 2m
10 ( ) ( ) ( ) 2 U 2m / 4 L U 2 L 2m / L 2 a πx cos a 2 x U dx cos a πx dx cos 2m / L 2 a x cos a 2 x U cos dx d a 2 m x dx cos L 2 E dxψ Hψ o 2 2 o 2 2 L 0 2 o L 0 2 2 2 L 0 L 0 o 2 2 2 = − − = − = − − = = ∫ ∫ ∫ ∫ + ∗ + + a a a π π π π π π π h h h h ( ) ( ) 2 U 2m / a x sin a 2 x U cos dx d a 2 m x dx sin L 2 E dxψ Hψ o 2 2 L 0 L 0 o 2 2 2 = + − − = = − ∫ ∫ − ∗ − − a i i π π π π h h k ε BZ 区 0 a π a π − ψ + ψ- ε o ε o+U o/2 ε o-U o/2 ( ) 2 m a/ 2 2 π ε h o =