试验次数 系数 (n) 2 3 1 3 3 1 4 14 6 4 1 心 .15 10 10 5 1 6 16 15 20 156 1 7 1721 35 35217 1 8 18 28 5670562881 9 .0. 193684126126843691 10 1104512021025221012045101 图7-2 杨辉三角模式图 筒历 返回总目录 返回章目绿口口>门结束 第7章二项分布与泊松分布 第25页
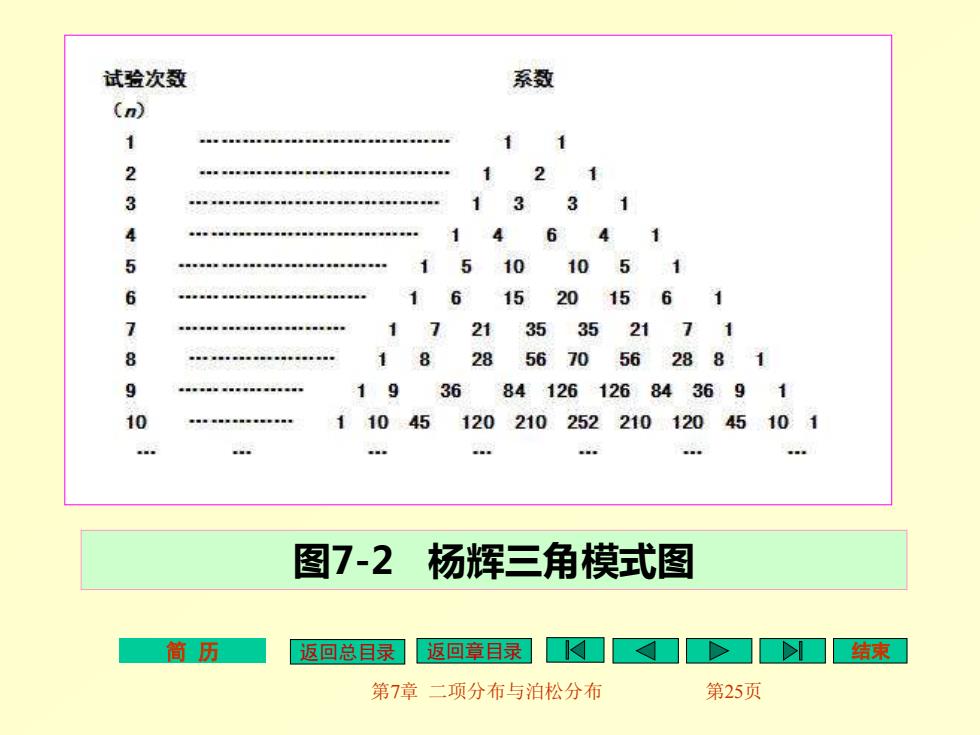
简 历 返回总目录 返回章目录 结束 第7章 二项分布与泊松分布 第25页 图7-2 杨辉三角模式图

杨辉三角的意义: 1.杨辉三角中每行有几个数字,表示展开式有几项 当试验次数为n时,有n+1项。 2.杨辉三角中每行中的数字表示展开式中每项的系 数大小。 3.杨辉三角中的各数字项及其数字的排列很有规律 可依照规律继续写下去。第一行的第一、第二项 均为数字1,以后每下一行的首项及末项均为1 中间各项为上一行相邻两项数字之和。 简历 返回总目录 返回章目录口口>]口结束 第7章二项分布与泊松分布 第26页
简 历 返回总目录 返回章目录 结束 第7章 二项分布与泊松分布 第26页 杨辉三角的意义: 1. 杨辉三角中每行有几个数字,表示展开式有几项。 当试验次数为n 时,有n+1项。 2. 杨辉三角中每行中的数字表示展开式中每项的系 数大小。 3. 杨辉三角中的各数字项及其数字的排列很有规律。 可依照规律继续写下去。第一行的第一、第二项 均为数字1,以后每下一行的首项及末项均为1, 中间各项为上一行相邻两项数字之和

五、二项分布的应用 二项分布在生物学及医学领域中,主要应用在下 列几个方面: ①总体率的可信区间估计, ②率的u检验:单样本及两样本比较。 ③样本率与总体率比较的直接计算概率法。 筒历 返回总目录 返回章目录]口>口结束 第7章二项分布与泊松分布 第27页
简 历 返回总目录 返回章目录 结束 第7章 二项分布与泊松分布 第27页 五、二项分布的应用 二项分布在生物学及医学领域中,主要应用在下 列几个方面: ① 总体率的可信区间估计, ② 率的u检验:单样本及两样本比较。 ③ 样本率与总体率比较的直接计算概率法

(一)应用二项分布计算概率 【例7.1】如出生男孩的概率P=0.5,出生女孩的 概率为(1-P)=0.5。在一个妇产医院里有3名产 妇分娩3名新生儿,其中男孩为X=0,1,2,3的概率 按公式(7.1)计算的结果列于表7-1的第(3)栏 中。 2.分析:根据题意,已知生育男孩为事件A,其概率 P(A)=0.5(即π=0.5);生育女孩为事件B,其 概率为P(B)=1-P(A)=1-0.5=0.5(即1- π=0.5)。 简历 返回总目绿 返回章目录口 结 第7章二项分布与泊松分布 第28页
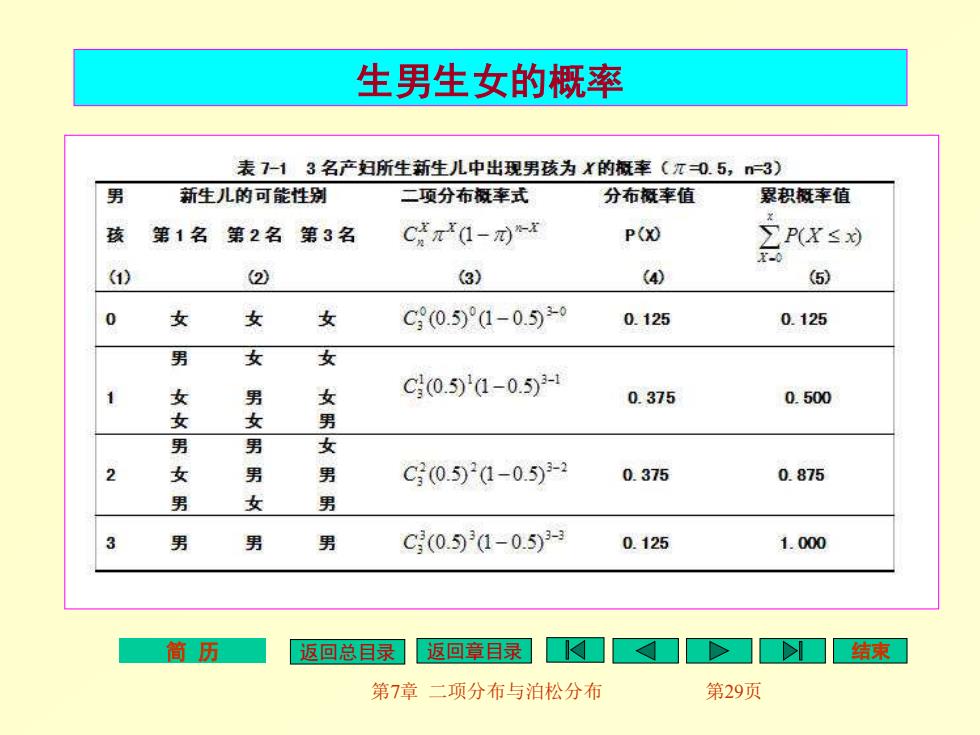
简 历 返回总目录 返回章目录 结束 第7章 二项分布与泊松分布 第28页 (一)应用二项分布计算概率 1. 【例7.1 】如出生男孩的概率P=0.5,出生女孩的 概率为(1-P)=0.5。在一个妇产医院里有3名产 妇分娩3名新生儿,其中男孩为X=0,1,2,3的概率 按公式(7.1)计算的结果列于表7-1的第(3)栏 中。 2. 分析:根据题意,已知生育男孩为事件A,其概率 P(A)=0.5(即π=0.5);生育女孩为事件B ,其 概率为P(B)=1-P(A)=1-0.5=0.5(即1- π=0.5)
生男生女的概率 表7-13名产妇所生新生儿中出现男孩为X的概率(π0.5,3) 罗 新生儿的可能性别 二项分布概率式 分布概幸值 累积概率值 孩 第1名第2名第3名 Cgπ21-刀x P(0 x (1) ② (3) 4④) (5) 0 女 女 女 C0.5)1-0.)20 0.125 0.125 男 女 女 1 女 男 女 C0.5)1-0.5)3- 0.375 0.500 女 女 男 男 男 女 2 女 男 男 C90.)21-0.5)-2 0.375 0.875 男 女 男 男 男 男 C(0.5)1-0.5)3月 0.125 1.000 筒历 返回总目录 返回章录口>口结束 第7章二项分布与泊松分布 第29页
简 历 返回总目录 返回章目录 结束 第7章 二项分布与泊松分布 第29页 生男生女的概率