
由公式(7.2)可看出二项展开式有以下特点: (4)二项分布的区间累积概率 设m1≤X≤m2,m1<m2),则X在m1至m2 区间的累积概率有: 1m2 Pn(m,≤X≤m2)=∑C,π*(1-z)-x X=m 筒历 返回总目录 返回章目录口>口结束 第7章二项分布与泊松分布 第15页
简 历 返回总目录 返回章目录 结束 第7章 二项分布与泊松分布 第15页 由公式(7.2)可看出二项展开式有以下特点: (4)二项分布的区间累积概率 设m1≤X≤m2 ,m1<m2), 则X在m1至m2 区间的累积概率有: = − = − 2 1 ( ) (1 ) 1 2 m X m X X n X Pn m X m Cn
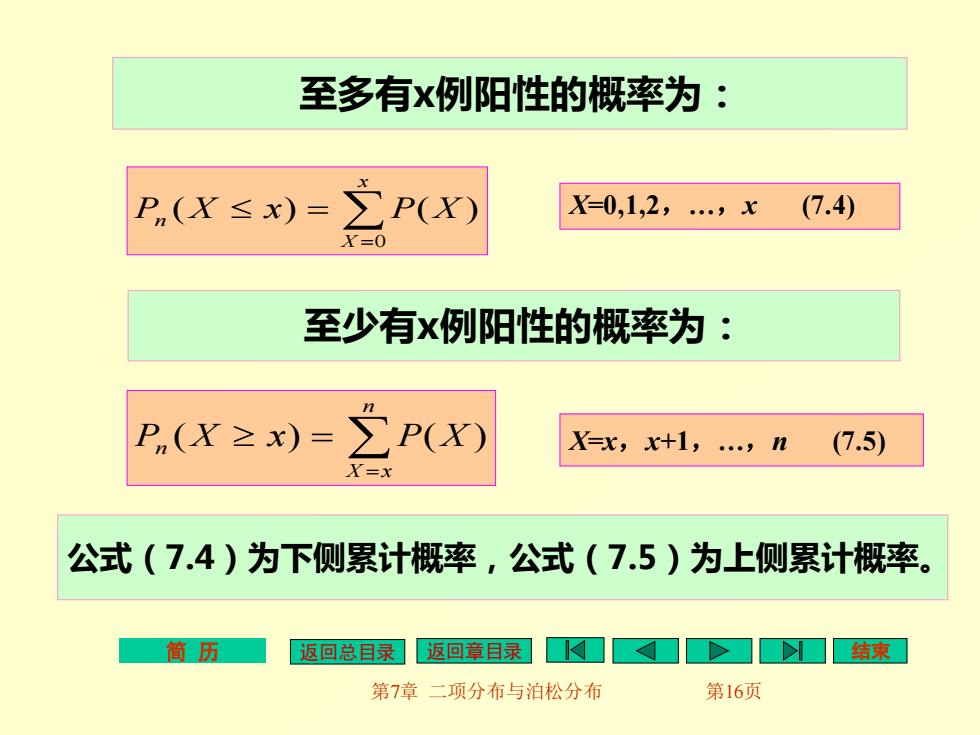
至多有x例阳性的概率为: P(X≤x)=∑P(X) X=0,1,2,.,x (7.4) X=0 至少有x例阳性的概率为: P,(X≥x)=∑P(X) X=x,x+1,.n (7.5) =x 公式(7.4)为下侧累计概率,公式(7.5)为上侧累计概率。 筒历 返回总目绿 返回章耳录4口>]口结束 第7章二项分布与泊松分布 第16页
简 历 返回总目录 返回章目录 结束 第7章 二项分布与泊松分布 第16页 至多有x例阳性的概率为: 至少有x例阳性的概率为: = = x X Pn X x P X 0 ( ) ( ) X=0,1,2,.,x (7.4) = = n X x Pn (X x) P(X ) X=x,x+1,.,n (7.5) 公式(7.4)为下侧累计概率,公式(7.5)为上侧累计概率

3.二项分布的概率分布图形 1. 以X为横坐标,P(X)为纵坐标,在坐 标纸上可绘出二项分布的图形,由于X为 离散型随机变量,二项分布图形由横坐 标上孤立点的垂直线条组成。 2. 二项分布的图形取决于π与n的大小。当 充分大时,二项分布趋向对称,可以证 明其趋向正态分布。 筒历 返回总目录 返回章目录]口>口结束 第7章二项分布与泊松分布 第17页
简 历 返回总目录 返回章目录 结束 第7章 二项分布与泊松分布 第17页 3.二项分布的概率分布图形 1. 以X为横坐标,P(X)为纵坐标,在坐 标纸上可绘出二项分布的图形, 由于X为 离散型随机变量,二项分布图形由横坐 标上孤立点的垂直线条组成。 2. 二项分布的图形取决于π与n的大小。当 n充分大时,二项分布趋向对称,可以证 明其趋向正态分布

3.二项分布的概率分布图形 3.nπ的大小与分布类型: ①当nπ之积大于5时,分布接近正态分布; ②当nπ<5时,图形呈偏态分布。 ③ 当π=0.5时,图形分布对称,近似正态。 ④ 如果π≠0.5或距0.5较远时,分布呈偏态。 见图7-1。 简历 返回总目录 返回章耳录4口>]口结束 第7章二项分布与泊松分布 第18页
简 历 返回总目录 返回章目录 结束 第7章 二项分布与泊松分布 第18页 3.二项分布的概率分布图形 3. nπ的大小与分布类型: ① 当nπ之积大于5时,分布接近正态分布; ② 当nπ<5时,图形呈偏态分布。 ③ 当π=0.5时,图形分布对称,近似正态。 ④ 如果π≠0.5或距0.5较远时,分布呈偏态。 见图7-1
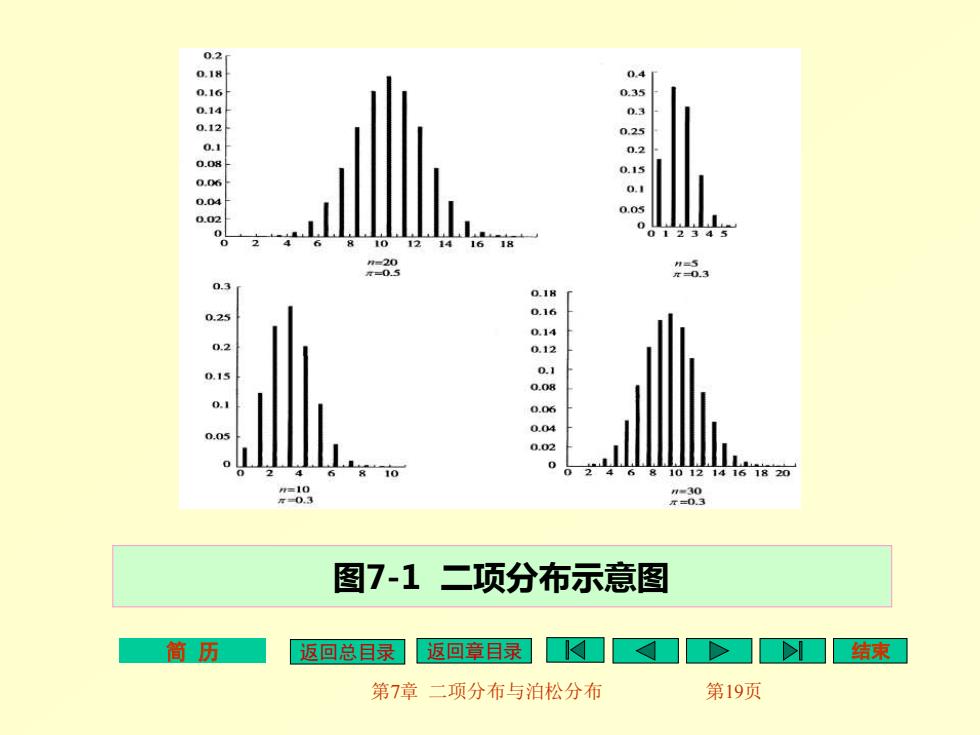
02 0.4 SEEEEE 0.0s 0.1H 025 0.16 0.14 02 012 0.15 0.06 0.04 0.02 161820 -9 图7-1二项分布示意图 筒历 返回总目录 返回章目录]口>口结束 第7章二项分布与泊松分布 第19页
简 历 返回总目录 返回章目录 结束 第7章 二项分布与泊松分布 第19页 图7-1 二项分布示意图