电子科技大学：《有限元理论与建模方法 Finite Element Analysis and Modeling》研究生课程教学资源（课件讲稿）第二章 有限元法的基本原理（平面问题有限元法）

网 Pe={Pex Pey Pez Ps=Psx Psy P) 原因 PPx Pw py {0}={0x0y0 结果 e3={ex ey? XV {dj=fu v wy 电子科技大学研究生课程 2020.9

电子科技大学研究生课程 2020.9 {P v }={pvx pvy pvz } T {P c }={ pcx pcy pcz } T {P s }={ psx psy psz } T {σ}={σ x σ y σ z τ xy τ yz τ zx } T {ε}={ε x ε y ε z ν xy ν yz ν zx } T {d}={u v w} T 原因 结果

例 杠 717717 717710 杠内部有没有应力？ 装配应力？ 热应力？ 电子科技大学研究生课程 2020.9

电子科技大学研究生课程 2020.9 杠内部有没有应力？ 装配应力？ 杠 热应力？

二、弹性力学的基本方程 例 Relationship among load,stress,strain and displacement ◆平衡方程 ◆几何方程 物理方程 电子科技大学研究生课程 2020.9

电子科技大学研究生课程 2020.9  平衡方程  几何方程  物理方程 二、弹性力学的基本方程 Relationship among load, stress, strain and displacement

1、平衡方程 例 应力~载荷 针对微分体3个方向的平衡 3个方程 o =0 =0 o +py=0 电子科技大学研究生课程 2020.9

电子科技大学研究生课程 2020.9 1、平衡方程                      0 0 0 vz xz yz z vy xy y yz vx x xy xz p x y z p x y z p x y z                   应力 ~ 载荷 针对微分体3个方向的平衡 3个方程

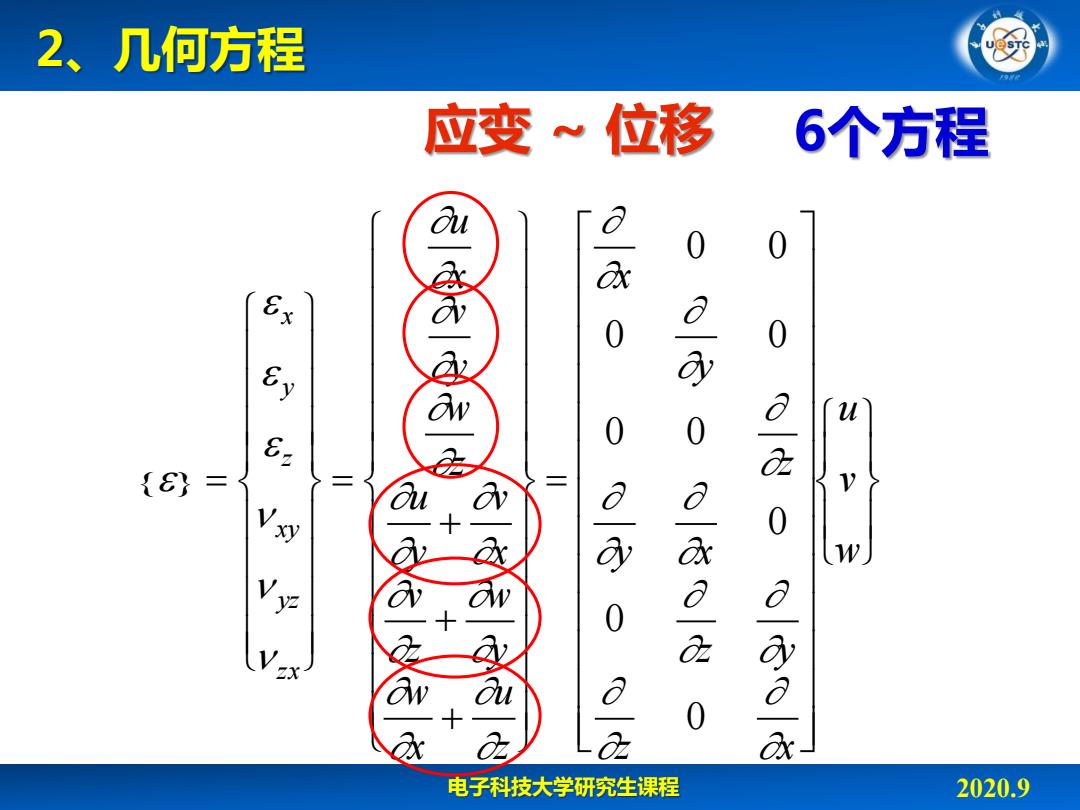
2、几何方程 应变~位移 6个方程 0 x Ex 0 0 0 a2 {} 0 /a2 0 0 电子科技大学研究生课程 2020.9

电子科技大学研究生课程 2020.9 2、几何方程                                                                                                     w v u z x z y y x z y x z u x w y w z v x v y u z w y v x u z x yz xy z y x                                            0 0 0 0 0 0 0 0 0 应变 ~ 位移 6个方程