
(2)分析乘性干扰c(t)的影响时,可把调制信 道分为两大类: 。 恒参信道,即c(t)随时间缓变或不变; ·随参信道,即c(t)随机快速变化。 。 通常,将架空明线、电缆、光导纡维、超短波 及微波视距传播、卫星审继等视为恒参信道。 西将短波患离层及射信道、各种散射信道、超 短波移动通信信道等视为随参信道。 2.编码信道模型 编码信道的特性可用信道转移概率(条件概 率)来描述。以二进制无记忆编码信道为例。 2011/11/13 6
• (2)分析乘性干扰 的影响时,可把调制信 道分为两大类: • 恒参信道,即 随时间缓变或不变; • 随参信道,即 随机快速变化。 • 通常,将架空明线、电缆、光导纤维、超短波 及微波视距传播、卫星中继等视为恒参信道。 而将短波电离层反射信道、各种散射信道、超 短波移动通信信道等视为随参信道。 2.编码信道模型 • 编码信道的特性可用信道转移概率(条件概 率)来描述。以二进制无记忆编码信道为例。 2011/11/13 6 c t( ) c t( ) c t( )
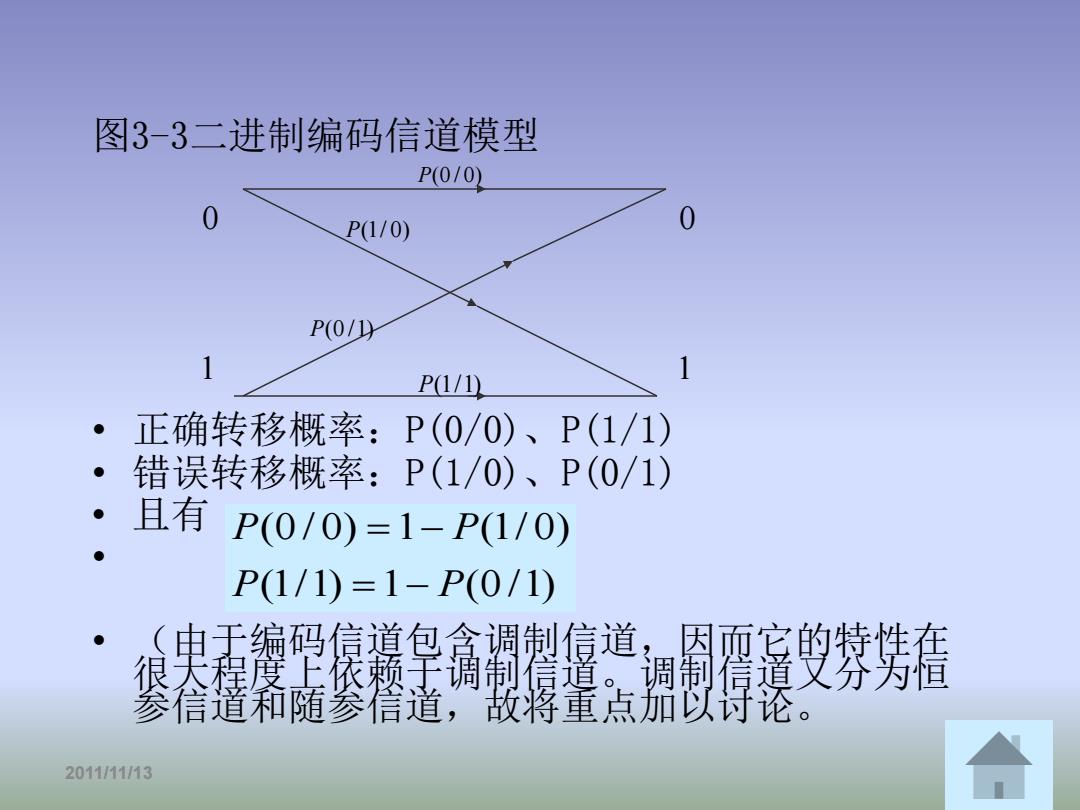
图3-3二进制编码信道模型 P(0/0) 0 P(1/0) 0 P(0/) P1/1 1 正确转移概率:P(0/0)、P(1/1) 。 错误转移概率:P(1/0)、P(0/1) 且有P(0/0)=1-P(1/0) ● P(1/1)=1-P(0/1) 尖囊卑高道度9棼美 参信道和随参信道,故将重点加以讨论。 2011/11/13
图3-3二进制编码信道模型 • 正确转移概率:P(0/0)、P(1/1) • 错误转移概率:P(1/0)、P(0/1) • 且有 • • (由于编码信道包含调制信道,因而它的特性在 很大程度上依赖于调制信道。调制信道又分为恒 参信道和随参信道,故将重点加以讨论。 2011/11/13 7 (1/1) 1 (0 /1) (0 / 0) 1 (1/ 0) P P P P = − = − 1 0 1 0 P(0 / 0) P(0 /1) P(1/ 0) P(1/1)

3.3、恒参信道的特性及其对信号的影响 。 恒参信道是指乘性干扰c(t)基本不随时间 变化的信道。因此,恒参信道可等效为 一个线性时不变网络。H(o)可用幅频特性 和相频特性共同来描述。 1.传输特性 H(@)=H(@e() ·幅频特性 H(@)~@ ·相频特性 0)心0 2011/11/13 8
3.3、恒参信道的特性及其对信号的影响 • 恒参信道是指乘性干扰 基本不随时间 变化的信道。因此,恒参信道可等效为 一个线性时不变网络。 可用幅频特性 和相频特性共同来描述。 1. 传输特性 • 幅频特性 • 相频特性 2011/11/13 8 c t( ) H(ω) ( ) () () j H He φ ω ω ω = H(ω) ~ ω φ(ω) ~ ω

·1.不失真条件 H(0)-Keior H(o)-o为一条水平线 ● p(ω)-o成线性关系 引入群迟延一频率特性,它定义为相频特性的 导数,即 x(ω)= do(o) dω 若(O)~0呈线性关系,则(@)~ω曲线是 一 条水平直线,如图3-4所示。这时,信号的不 同频率成分将有相同的时延,因而信号经过该 信道传输后将不发生失真。 2011/11/13 9
• 1.不失真条件 • • • 引入群迟延—频率特性,它定义为相频特性的 导数,即 • 若 呈线性关系,则 曲线是一 条水平直线,如图3-4所示。这时,信号的不 同频率成分将有相同的时延,因而信号经过该 信道传输后将不发生失真。 2011/11/13 9 ( ) ( ) ( ) j t H Ke H ω ω ω ω ϕω ω = − − 为一条水平线 成线性关系 ω φ ω τ ω d d ( ) ( ) = φ(ω) ~ ω τ (ω) ~ ω
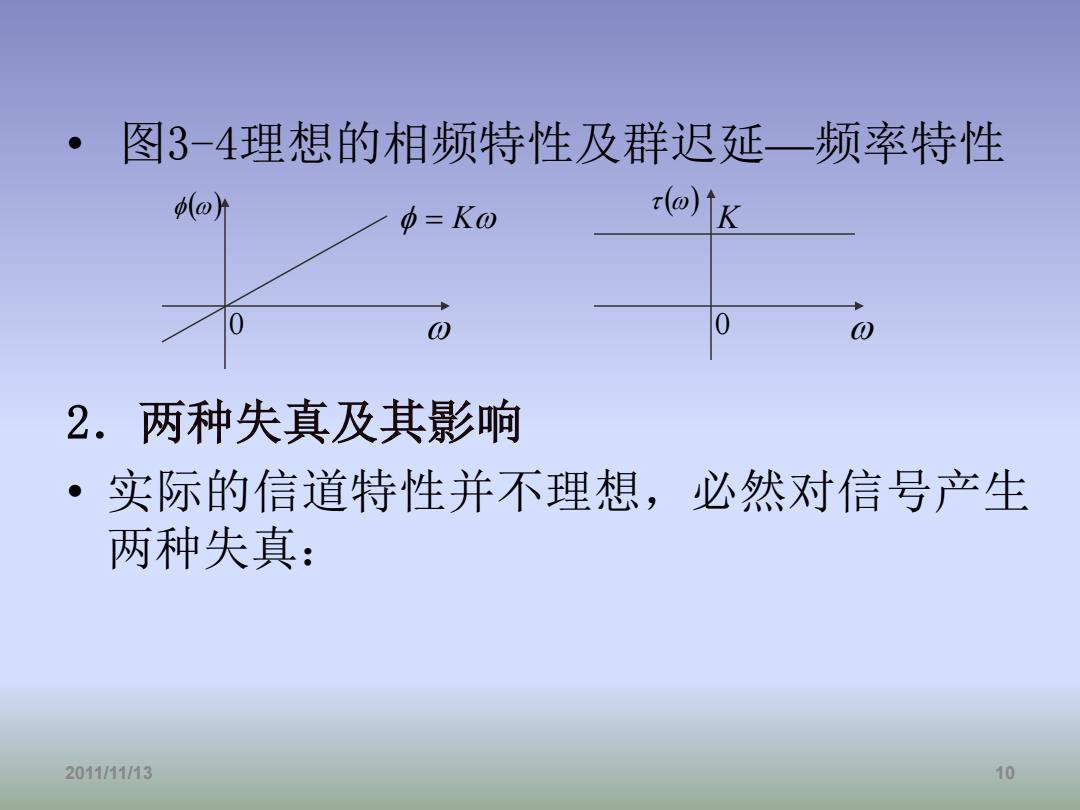
·图3-4理想的相频特性及群迟延一频率特性 =Ko r(@)iK 0 0 2.两种失真及其影响 实际的信道特性并不理想,必然对信号产生 两种失真: 2011/11/13 10
• 图3-4理想的相频特性及群迟延—频率特性 2.两种失真及其影响 • 实际的信道特性并不理想,必然对信号产生 两种失真: 2011/11/13 10 φ(ω) τ (ω) 0 0 K ω ω φ = Kω