广东工业大学：《通信电路与系统》课程教学资源（课件讲义）第二章 高频基础电路 第一节 选频网络

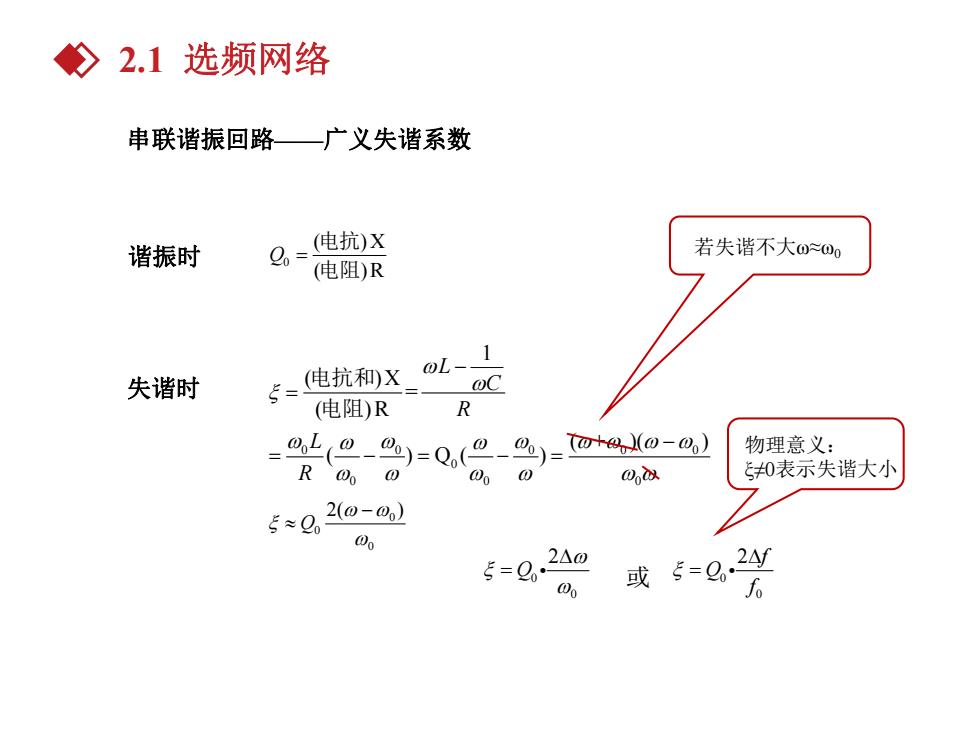
◇2.1选频网络 串联谐振回路—广义失谐系数 谐振时 Q,=电抗x 若失谐不大00 (电阻)R 失谐时 5=电抗和X oL、1 C (电阻)R R -4(9-)=0,(巴-%)-0-】 物理意义： R@o 000 0d议 0表示失谐大小 50,2a-@) @n 2△0 5=0。 00 或5=0,8

串联谐振回路——广义失谐系数 0 ( )X ( )R Q  电抗 电阻 0 0 0 0 0 0 0 0 0 1 ( )X = ( )R ( + )( ) ( ) Q ( ) L C R L R                           电抗和 电阻 谐振时 失谐时 若失谐不大ω≈ω0 0 0 0 2( ) Q       0 0 2 Q       0 0 2 f Q f   或   物理意义： ξ≠0表示失谐大小 2.1 选频网络

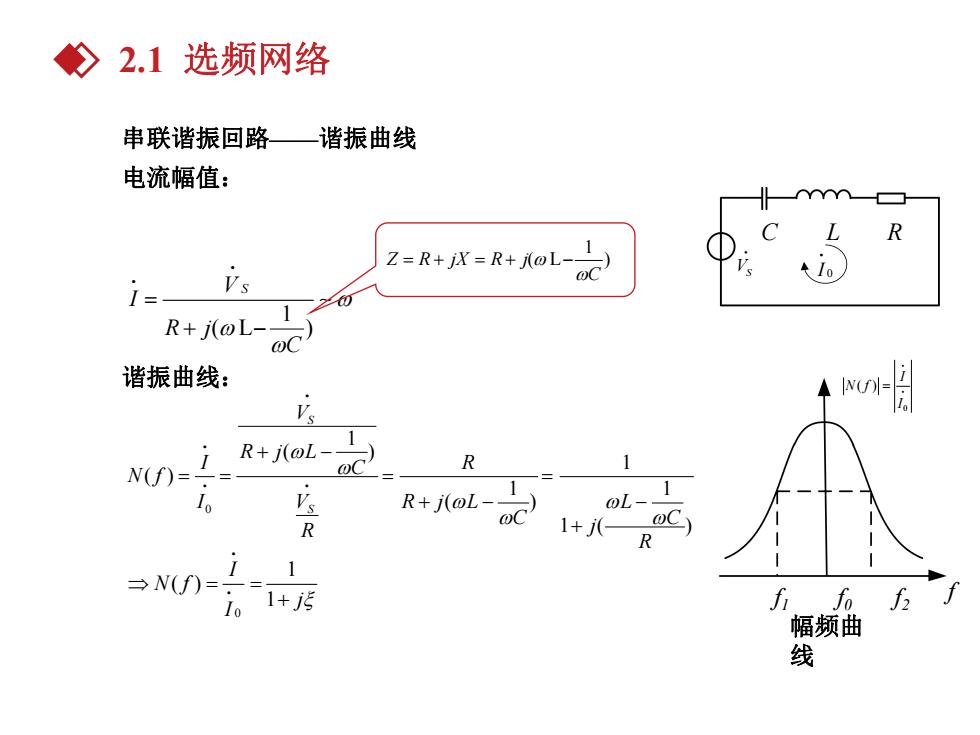
2.1选频网络 串联谐振回路一 谐振曲线 电流幅值： R Z=R+jX=R+j@L--) Vs OC ←Io 1= 20 R+j(@L-- 谐振曲线： V's N(-i R+j(@L-I R s R+j(OL-1 oL- R 1+j R →N(f)= i1 1+污 f fo f2 幅频曲 线

串联谐振回路——谐振曲线 电流幅值： 1 ( L ) V S I R j C          C L R VS  I 0  谐振曲线： 0 1 ( ) 1 ( ) 1 1 ( ) 1 ( ) S S V R j L I C R N f I V R j L L C C R j R                     0 1 ( ) 1 I N f j I        幅频曲 线 0 ( ) I N f I    f1 f0 f2 f 1 Z R jX R j( L ) C        2.1 选频网络

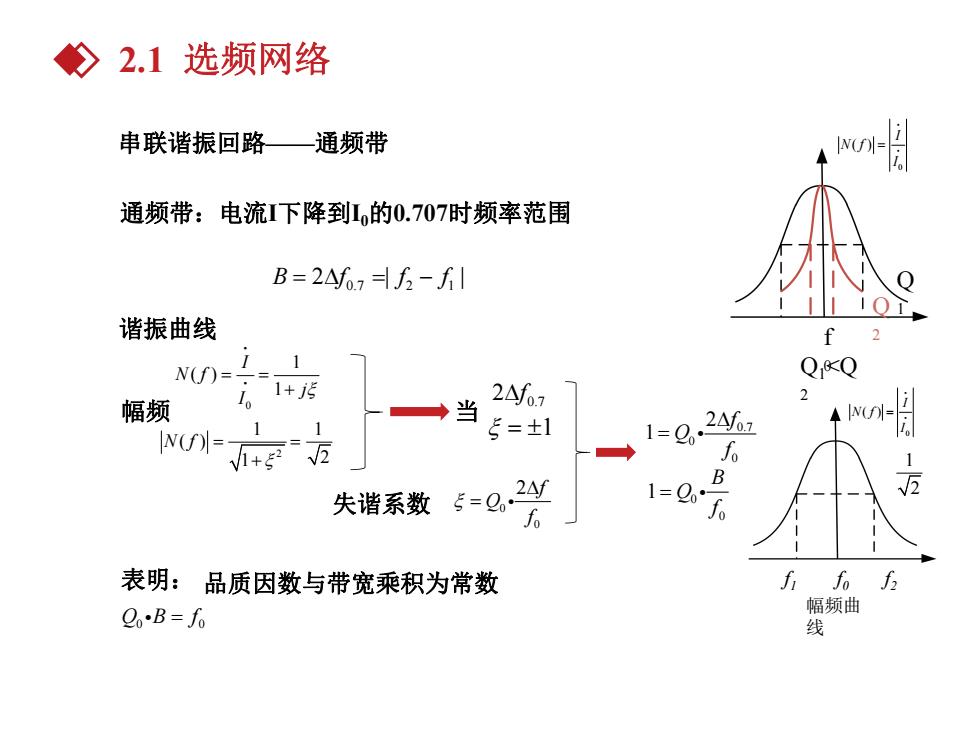
父2.1选频网络 串联谐振回路—通频带 i N(f)= 通频带：电流下降到1的0.707时频率范围 B=2△f6,5-fI 谐振曲线 f N(f)= 1 QQ 2 幅频 。1+ ◆ 当 2△f07 ◆N(f- 1 5=1 1=Q244 失谐系数 5=g24 1=0o o 表明：品质因数与带宽乘积为常数 fr fo f2 2oB=fo 幅频曲

串联谐振回路——通频带 通频带：电流I下降到I0的0.707时频率范围 0.7 2 1 B  2f | f  f | 谐振曲线 0 1 ( ) 1 I N f j I       2 1 1 ( ) 1 2 N f     幅频 0.7 2f   1 当 失谐系数 0 0 2 f Q f     表明： Q0 B 0   f 品质因数与带宽乘积为常数 f 0 0 ( ) I N f I   Q Q 1 2 Q1<Q 2 0.7 0 0 2 1 f Q f    0 0 1 B Q f   幅频曲 线 0 ( ) I N f I    f1 f0 f2 1 2 2.1 选频网络