
目录 5.1 概述与反馈型LC振荡原理 5.2 反馈型LC振荡电路 5.3 振荡器的频率稳定原理和高稳定度的LC振荡器 5.4 晶体振荡电路
目录 5.1 概述与反馈型LC振荡原理 5.2 反馈型LC振荡电路 5.3 振荡器的频率稳定原理和高稳定度的LC振荡器 5.4 晶体振荡电路

◇5.3振荡器的频率稳定原理 一、频率稳定度的定义 频率稳定度在数量上通常用频率偏差来表示。 频率偏差是指振荡器的实际工作频率和标称频率之间的偏差。它可 分为绝对偏差和相对偏差。 设f为实际振荡频率,f。为指定标称频率,则 1、绝对频率偏差:△f=f-f 绝对频率准确度 2、相对频率偏差:Y-/-1」 f。 f 相对频率准确度 3、频率稳定度的定义: 在一定时间间隔内,振荡器相对频率偏差的最大值,用3 表示。该数值越小越好,稳定性越高。 4、三种常用的频率稳定度 长期频率稳定度:一般指一天以上甚至数月的时间间隔内的相对频率变化的 最大值。这种变化通常是由振荡器中元器件老化而引起的。 短期频率稳定度:一般指一天以内,以小时、分或秒计算的时间间隔的频率 相对变化。产生这种频率不稳的因素有温度、电源电压等。 瞬时频率稳定度:一般指秒或毫秒时间间隔内的频率相对变化。引起这类频 率不稳定的主要因素是振荡器内部噪声
一、频率稳定度的定义 5.3 振荡器的频率稳定原理 频率稳定度在数量上通常用频率偏差来表示。 频率偏差是指振荡器的实际工作频率和标称频率之间的偏差。它可 分为绝对偏差和相对偏差。 设 f 为实际振荡频率,fc 为指定标称频率,则 1、绝对频率偏差: 2、相对频率偏差: c f f f c c c f f f f f | | 3、频率稳定度的定义: 在一定时间间隔内,振荡器相对频率偏差的最大值,用 表示。该数值越小越好,稳定性越高。 max c f f 时间间隔 绝对频率准确度 相对频率准确度 4、三种常用的频率稳定度 长期频率稳定度:一般指一天以上甚至数月的时间间隔内的相对频率变化的 最大值。这种变化通常是由振荡器中元器件老化而引起的。 短期频率稳定度:一般指一天以内,以小时、分或秒计算的时间间隔的频率 相对变化。产生这种频率不稳的因素有温度、电源电压等。 瞬时频率稳定度:一般指秒或毫秒时间间隔内的频率相对变化。引起这类频 率不稳定的主要因素是振荡器内部噪声
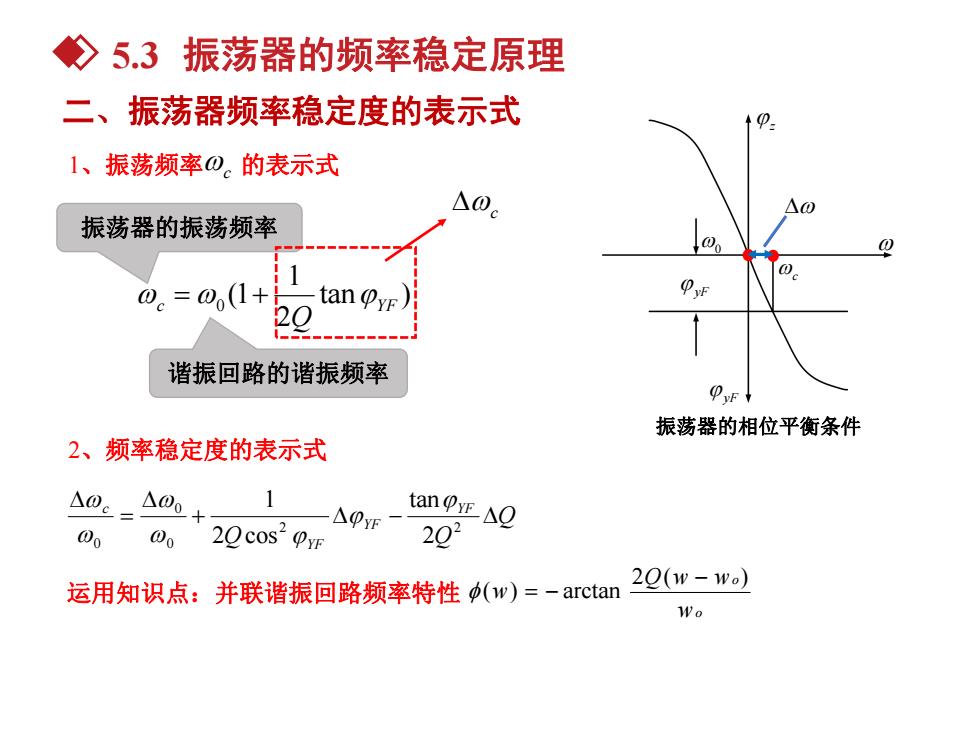
◇5.3振荡器的频率稳定原理 二、振荡器频率稳定度的表示式 1、振荡频率0。的表示式 △0 振荡器的振荡频率 0 0。=0(1+ tan PyF) 谐振回路的谐振频率 振荡器的相位平衡条件 2、频率稳定度的表示式 △0e_△0+ 1 一△pyF tan pyE△Q 00 @o 20cos2 Oyn 202 运用知识点:并联谐振回路频率特性(w)=-arctan 20(w-Wo) Wo
振荡器的相位平衡条件 z 0 yF yF c 二、振荡器频率稳定度的表示式 振荡器的振荡频率 谐振回路的谐振频率 2、频率稳定度的表示式 tan ) 2 1 (1 c 0 YF Q Q Q Q YF YF YF c 2 2 0 0 0 2 tan 2 cos 1 运用知识点:并联谐振回路频率特性 o o w Q w w w 2 ( ) ( ) arctan 1、振荡频率 c 的表示式 c 5.3 振荡器的频率稳定原理
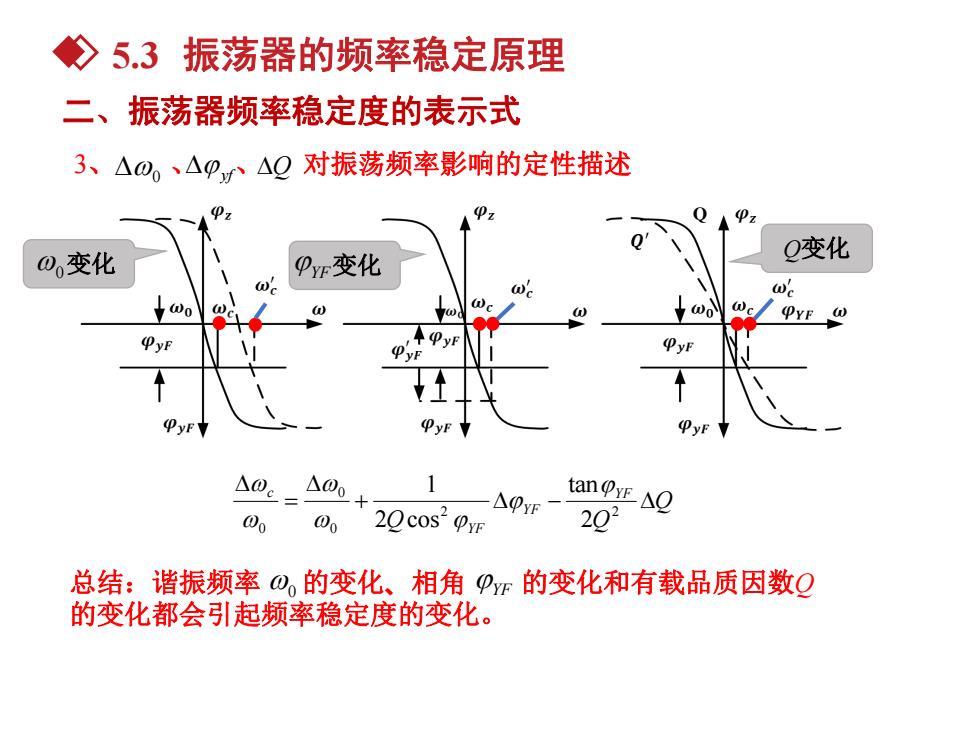
◇5.3振荡器的频率稳定原理 二、振荡器频率稳定度的表示式 3、△0,、△p,r、△Q对振荡频率影响的定性描述 0 (z 0,变化 Q变化 PF变化 @o ωo △0。_A00 一△F一 anyE△g 00 20cos yE 202 总结:谐振频率⊙,的变化、相角pF的变化和有载品质因数Q 的变化都会引起频率稳定度的变化
Q Q变化 Q Q Q YF YF YF c 2 2 0 0 0 2 tan 2 cos 1 0变化 YF 变化 总结:谐振频率 的变化、相角 的变化和有载品质因数Q 的变化都会引起频率稳定度的变化。 0 YF 3、 0 、 yf、 Q 对振荡频率影响的定性描述 5.3 振荡器的频率稳定原理 二、振荡器频率稳定度的表示式

◇5.3振荡器的频率稳定原理 三、引起频率不稳的原因 1、温度变化会引起L、C和晶体管参数变化。 2、湿度变化会引起L、Q变化。 3、电源电压变化会引起晶体管参数变化。 4、机械振动会引起L的变化。 结论:引起振荡器频率不稳定的外部因素是温度、湿度、电源电 压波动和机械振动。这些外因变化会引起△0。△p、△Q的变 化。因此产生频率不稳定
三、引起频率不稳的原因 1、温度变化会引起L、C和晶体管y参数变化。 2、湿度变化会引起L、Q变化。 3、电源电压变化会引起晶体管参数变化。 4、机械振动会引起L的变化。 结论:引起振荡器频率不稳定的外部因素是温度、湿度、电源电 压波动和机械振动。这些外因变化会引起 的变 化。因此产生频率不稳定。 0、YF、Q 5.3 振荡器的频率稳定原理