广东工业大学：《通信电路与系统》课程教学资源（课件讲义）第二章 高频基础电路 第一节 选频网络

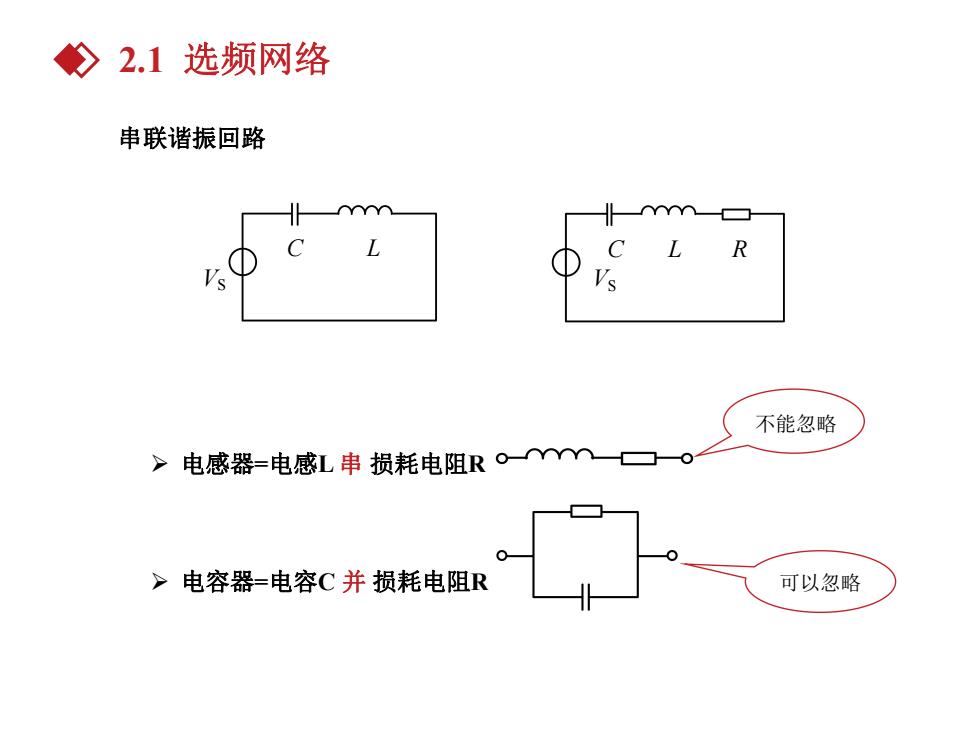
父2.1选频网络 串联谐振回路 R 不能忽略 >电感器=电感L串损耗电阻R。一☐o >电容器=电容C并损耗电阻R 可以忽略

串联谐振回路 Ø 电感器=电感L 串 损耗电阻R Ø 电容器=电容C 并 损耗电阻R C L VS VS C L R 不能忽略 可以忽略 2.1 选频网络

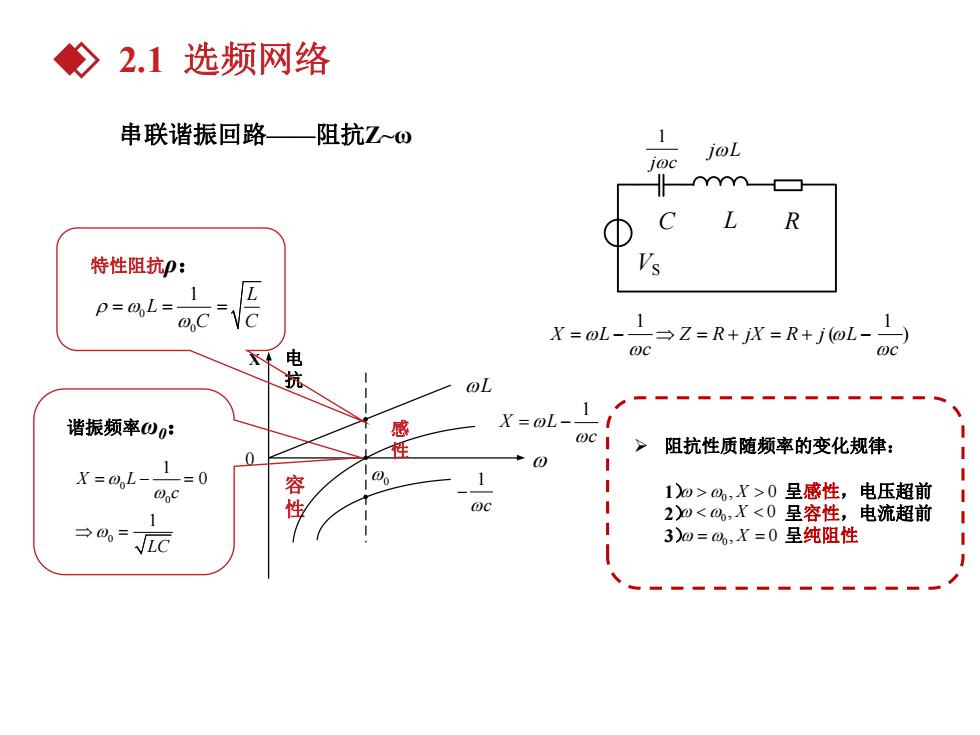
◇2.1选频网络 串联谐振回路—阻抗Zω 1 joL joc D C R 特性阻抗p: s 1 p=0L= DC Y=@L-- Z=R+X=R+1(@L- 电 @c 抗 ol 谐振频率00： 感 Oc I 阻抗性质随频率的变化规律： 1 0 *0 X=0,L- =0 1 Wc 容 1)0>,X>0呈感性，电压超前 Oc 1 2)0<,X<0呈容性，电流超前 →00= √LC 3)0=0,X=0呈纯阻性

串联谐振回路——阻抗Z~ω X 容 性 感 性 电 抗 1 X L c     L  1 c  0 0 1 1 X L Z R jX R j ( L ) c c             Ø 阻抗性质随频率的变化规律： 1） 呈感性，电压超前 2） 呈容性，电流超前 3） 呈纯阻性 0    , X  0 0    , X  0 0    , X  0 0 0 1 L L C C       特性阻抗ρ： 0 0 0 1 0 1 X L c LC         谐振频率ω0： VS C L R 1 jc jL 2.1 选频网络

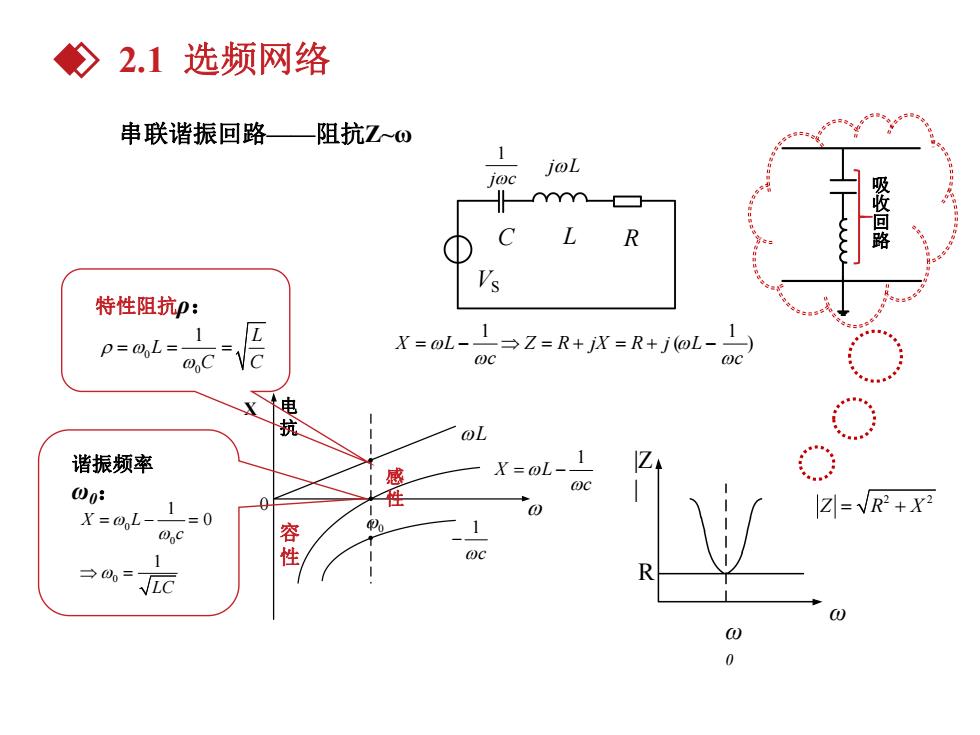
2.1选频网络 串联谐振回路—阻抗☑~o 1 joL joc R 吸收回路 特性阻抗p: 1 p=0L= X=0L-L>Z=R+jX=R+j(@L-1) @,C X 抗 oL 谐振频率 1 X=0L- 00: 性 X=0,L- 1 -=0 0 Z=VR+X 0,C 1 容性 →00= LC ① 2

串联谐振回路——阻抗Z~ω X 容 性 感 性 电 抗 1 X L c     L  1 c  0 0 1 1 X L Z R jX R j ( L ) c c             0 0 1 L L C C       特性阻抗ρ： 0 0 0 1 0 1 X L c LC         谐振频率 ω0： VS C L R 1 jc jL |Z | R ω 0 ω 2 2 Z  R  X 吸 收 回 路 2.1 选频网络

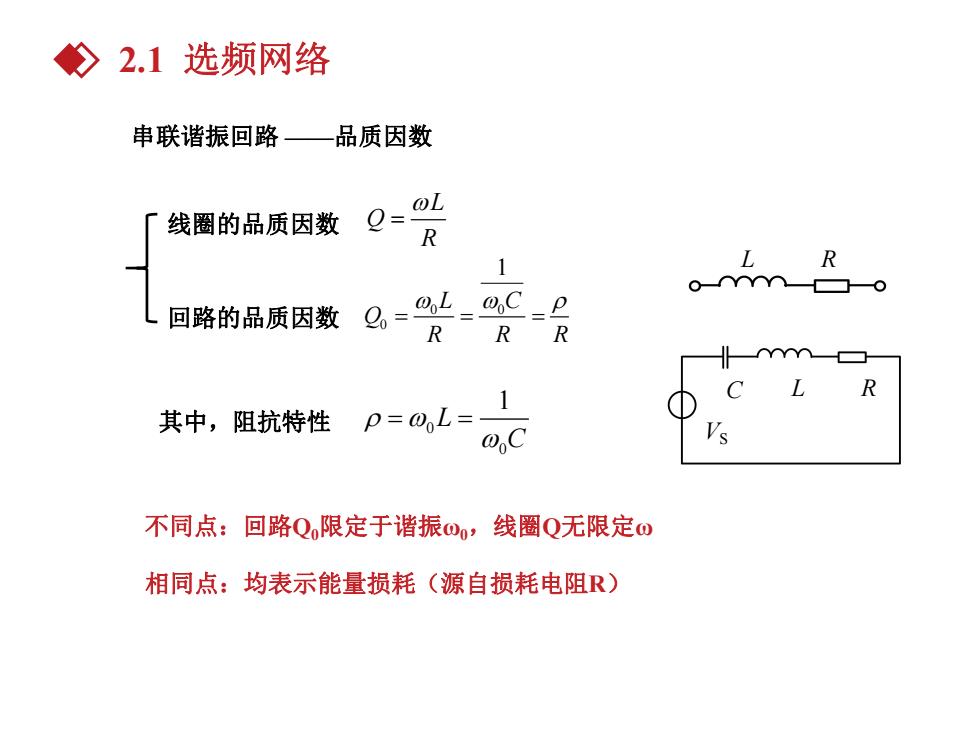
父2.1选频网络 串联谐振回路一品质因数 OL 线圈的品质因数 Q≈ R 1 L R 回路的品质因数 Q=4L=OC=e R 其中，阻抗特性 @C 不同点：回路Q限定于谐振o0,线圈Q无限定o 相同点：均表示能量损耗（源自损耗电阻R)

串联谐振回路 ——品质因数 VS C L R 线圈的品质因数 L Q R   L R 0 0 0 1 L C Q R R R       其中，阻抗特性 0 0 1 L C      不同点：回路Q0限定于谐振ω0，线圈Q无限定ω 相同点：均表示能量损耗（源自损耗电阻R） 回路的品质因数 2.1 选频网络

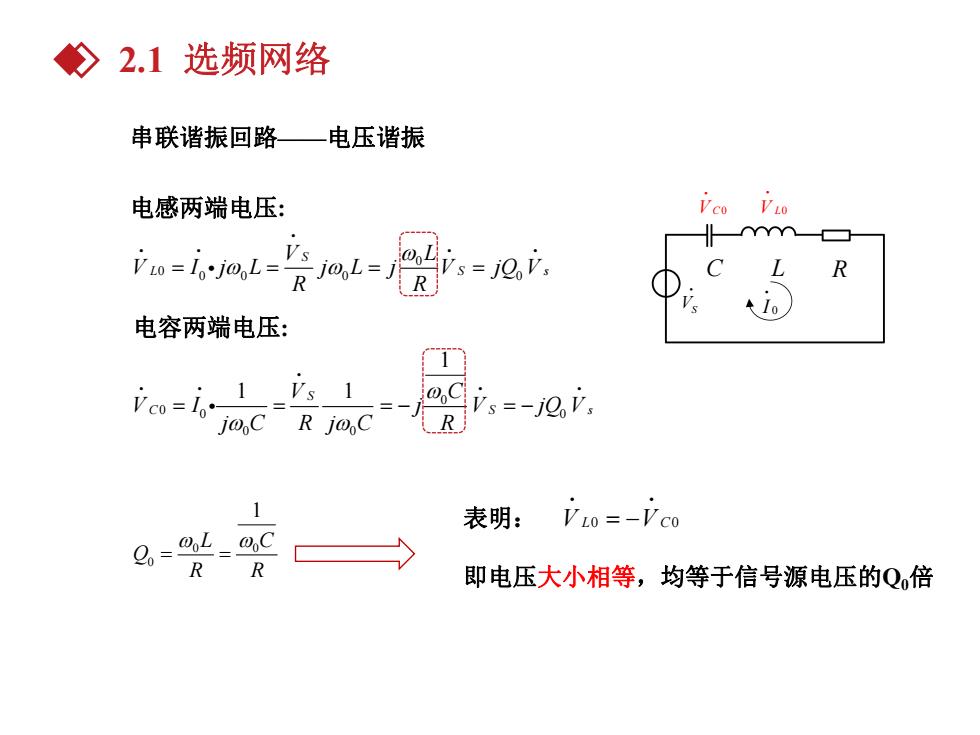
2.1选频网络 串联谐振回路一电压谐振 电感两端电压： Vio=lojoL-Vs =j0y R 电容两端电压： Vs=-jQV. joC R j@C R 1 表明：Vo=-Vco 即电压大小相等，均等于信号源电压的Q倍

串联谐振回路——电压谐振 0 0 0 0 0 0 S L S s V L V I j L j L j V jQ V R R              0 0 0 0 0 0 1 1 S 1 C S s V C V I j V jQ V j C R j C R                电感两端电压: 电容两端电压: C L R VS  I 0  V C0  V L0  0 0 0 1 L C Q R R     表明： 即电压大小相等，均等于信号源电压的Q0倍 V L0  V C0   2.1 选频网络