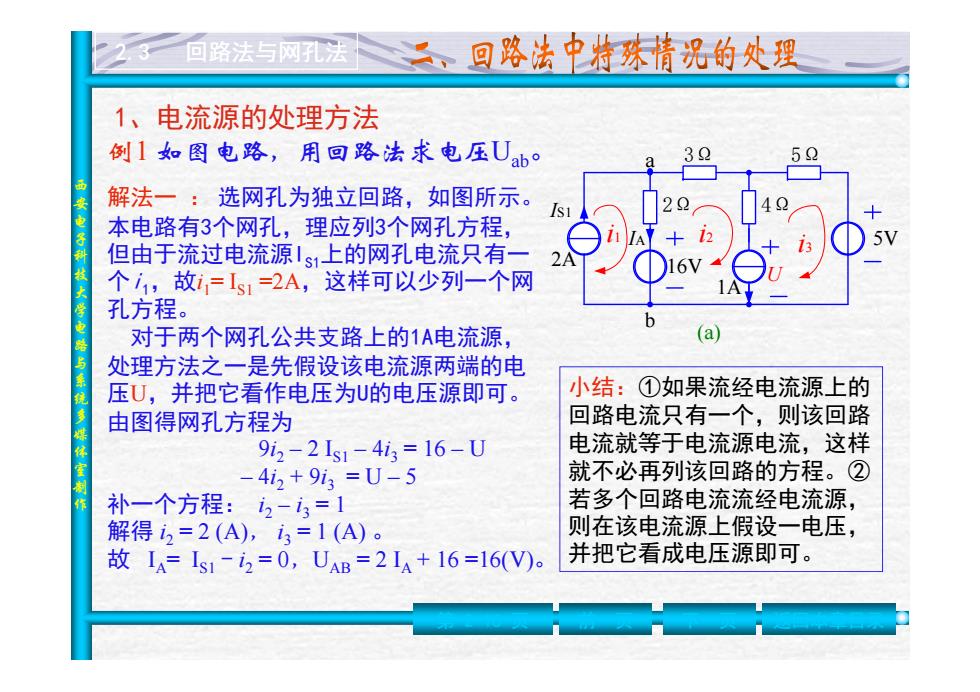
回路法与网孔法 二、回路法中特殊情况的处理 1、电流源的处理方法 倒1如图电路,用回路法求电压Uab。 32 解法一:选网孔为独立回路,如图所示。 本电路有3个网孔,理应列3个网孔方程, 但由于流过电流源1s1上的网孔电流只有一 个1,故=1s1=2A,这样可以少列一个网 孔方程。 对于两个网孔公共支路上的1A电流源, (a) 处理方法之一是先假设该电流源两端的电 压U,并把它看作电压为U的电压源即可。 小结:①如果流经电流源上的 由图得网孔方程为 回路电流只有一个,则该回路 9i2-21s1-4i3=16-U 电流就等于电流源电流,这样 -4i2+9i3=U-5 就不必再列该回路的方程。② 补一个方程:2-3=1 若多个回路电流流经电流源, 解得i=2(A),3=1(A)。 则在该电流源上假设一电压, 故A=151-2=0,UAB=21A+16=16(V)。 并把它看成电压源即可
西安电子科技大学电路与系统多媒体室制作 2.3 回路法与网孔法 例 1 如图电路,用回路法求电压 Uab 。 a b IS1 2A 16V 3Ω 2Ω 1A 4Ω 5Ω i1 i 2 i 3 5V (a) U IA 解法一 : 选网孔为独立回路,如图所示。 本电路有3个网孔,理应列3个网孔方程, 但由于流过电流源IS1上的网孔电流只有一 个 i1,故 i1= IS1 =2A,这样可以少列一个网 孔方程。 对于两个网孔公共支路上的1A电流源, 处理方法之一是先假设该电流源两端的电 压 U,并把它看作电压为U的电压源即可。 由图得网孔方程为 9 i 2 – 2 IS1 – 4 i 3 = 16 – U – 4 i 2 + 9 i 3 = U – 5 补一个方程: i 2 – i 3 = 1 解得 i 2 = 2 (A), i 3 = 1 (A) 。 故 I A= IS1 - i 2 = 0,UAB = 2 I A + 16 =16(V) 。 小结:①如果流经电流源上的 回路电流只有一个,则该回路 电流就等于电流源电流,这样 就不必再列该回路的方程。② 若多个回路电流流经电流源, 则在该电流源上假设一电压, 并把它看成电压源即可。 第 2-16 页 前一页 下一页 返回本章目录 1、电流源的处理方法
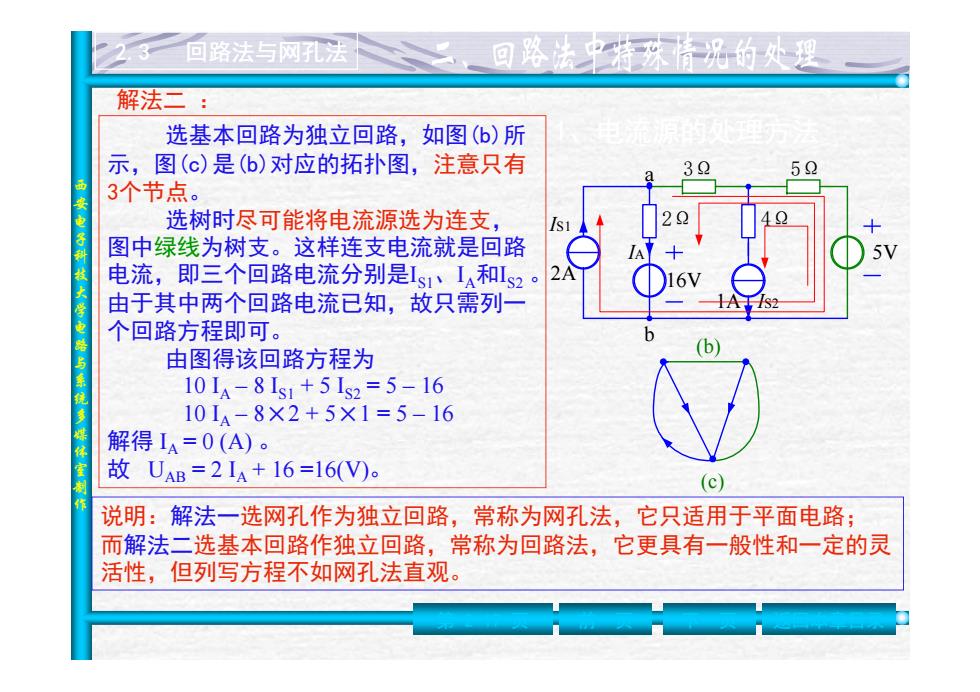
回路法与网孔法 解法二: 选基本回路为独立回路,如图(6)所 示,图(c)是(6)对应的拓扑图,注意只有 32 5 3个节点。 选树时尽可能将电流源选为连支, 1 图中绿线为树支。这样连支电流就是回路 电流,即三个回路电流分别是Is1、I和ls2 由于其中两个回路电流已知,故只需列一 个回路方程即可。 由图得该回路方程为 10IA-8Is1+5Is2=5-16 101a-8×2+5×1=5-16 解得IA=0(A)。 故UAB=2IA+16=16(V)。 (c) 说明:解法一选网孔作为独立回路,常称为网孔法,它只适用于平面电路; 而解法二选基本回路作独立回路,常称为回路法,它更具有一般性和一定的灵 活性,但列写方程不如网孔法直观
西安电子科技大学电路与系统多媒体室制作 2.3 回路法与网孔法 选基本回路为独立回路,如图(b)所 1、电流源的处理方法 示,图(c)是(b)对应的拓扑图,注意只有 3个节点 。 选树时尽可能将电流源选为连支, 图中绿线为树支。这样连支电流就是回路 电流,即三个回路电流分别是 IS1、I A 和 IS2 。 由于其中两个回路电流已知,故只需列一 个回路方程即可。 由图得该回路方程为 10 I A – 8 IS1 + 5 IS2 = 5 – 16 10 I A – 8 ×2 + 5 ×1 = 5 – 16 解得 I A = 0 (A) 。 故 UAB = 2 I A + 16 =16(V) 。 a b IS1 2A 16V 3Ω 2Ω 1A 4Ω 5Ω 5V (b) IS2 IA (c) 说明:解法一选网孔作为独立回路,常称为网孔法,它只适用于平面电路; 而解法二选基本回路作独立回路,常称为回路法,它更具有一般性和一定的灵 活性,但列写方程不如网孔法直观。 第 2-17 页 前一页 下一页 返回本章目录 解法二 :

回路法与网法 处 2、受控源的处理方法例2如图电路,用回路法求电压山。 0.1u 解:本例中含受控源(VCCS),处理方 法是:先将受控源看成独立电源。这样, 6 该电路就有两个电流源,并且流经其上 22 的回路电流均只有一个;故该电流源所 在回路电流己知,就不必再列它们的回 200 路方程了。如图中所标回路电流,可知: 92 42 =0.1u,i3=4 对回路2列方程为 小结:对受控源首先将它 26i2-2i1-20i13=12 看成独立电源;列方程后, 上述一些方程中会出现受控源的控制变 再补一个方程将控制量用 量u,用回路电流表示该控制变量,有 回路电流表示。 u=20(i3-i2) 解得i2=3.6(A),u=8(V)
西安电子科技大学电路与系统多媒体室制作 2.3 回路法与网孔法 例 2 如图电路,用回路法求电压 u 。 u 20Ω i1 0.1 u i 2 i 3 2Ω 9Ω 4Ω 6V 12V 4A 解 : 本例中含受控源(VCCS),处理方 法是:先将受控源看成独立电源。这样, 该电路就有两个电流源,并且流经其上 的回路电流均只有一个;故该电流源所 在回路电流已知,就不必再列它们的回 路方程了。如图中所标回路电流,可知: i1= 0.1 u, i 3 = 4 对回路 2列方程为 26 i 2 – 2 i1 – 20 i 3 = 12 上述一些方程中会出现受控源的控制变 量 u,用回路电流表示该控制变量,有 u = 20( i 3 – i 2 ) 解得 i 2 = 3.6 (A),u = 8 (V) 。 小结:对受控源首先将它 看成独立电源;列方程后, 再补一个方程将控制量用 回路电流表示。 第 2-18 页 前一页 下一页 返回本章目录 2、受控源的处理方法

2.4节点法Nodal Analysi$ 节点法是为了减少方程个数、简便手工计算过程的又一类改进方法。 一、节点法 1、节点法定义:以节点电压为未知变量列出并求解方程的方法称为节点法。 2、节点电压的概念 在电路中任意选择一个节点为参考节点, 其余节点与参考节点之间的电压,称为节点电 G2 压或节点电位,各节点电压的极性均以参考节 G3 点为“-”极。 如图电路,选节点4作参考点,其余各节 点的电压分别记为山1、和山3。支路电压可用 6 节点电压表示为:山12=山12,l23=4 u13=u1-2W3,414=u1y424=2,l34=u3 对电路的任意回路,如回路A,有 节点电压的独立性 和完备性。 413-山23-山12 =u1山3-(2-3)-(u12)≡0所以,节点电压自动满足KVL方程
西安电子科技大学电路与系统多媒体室制作 节点法是为了减少方程个数、简便手工计算过程的又一类改进方法。 2、节点电压的概念 在电路中任意选择一个节点为参考节点, 其余节点与参考节点之间的电压,称为节点电 压 或节点电位,各节点电压的极性均以参考节 点为“ - ”极。 如图电路,选节点 4作参考点,其余各节 点的电压分别记为 u1、u 2 和 u 3。支路电压可用 节点电压表示为: u12 = u1- u 2, u23 = u 2 - u 3 , u13 = u1- u 3, u14 = u1, u24 = u 2, u34 = u 3, 对电路的任意回路,如回路 A,有 u13 – u23 – u12 = u1- u3 – ( u 2 - u 3 ) – ( u1- u 2 ) ≡ 0 i 4 G 1 G 2 G 4 G 6 1 i 2 iS2 i 5 A G 3 G 5 iS4 iS6 2 3 4 i1 i3 i 6 第 2-19 页 前一页 下一页 返回本章目录 节点电压的独立性 和完备性 。 1、节点法定义:以节点电压为未知变量列出并求解方程的方法称为节点法 。 所以,节点电压自动满足KVL方程

节点法 节点法 3、节点法方程的列写规律 如图电路,在节点1,2,3分别列出KCL方程:(设 流出取正) G2 i1+i2+is2+i4-is4=0 3 3+5-2-is2=0 6+is6-i-i3=0 利用0L各电阻上的电流可以用节点电压表示为 i1=G1(山1-43),i2=G2(41-2),i3=G3(w2-3), i4=G441,i5=G5山2,i6=G643 代入KCL方程,合并整理后得 节点(1)(G1+G2+G4)u1 u2 Gu3=is4-is2 G11 G12 G13 (Σl) 节点(2) G241+(G2+G3+G)u2 G22 品zg。 节点(3) G141 -G3u2+(G1+G3+G6)43=-is6 6g1 Gg2 633 (Σl)3
西安电子科技大学电路与系统多媒体室制作 2.4 节点法 i 4 G 1 G 2 G 4 G 6 1 i 2 iS2 i 5 G 3 G 5 iS4 iS6 2 3 4 i1 i 3 i 6 如图电路, 在节点1,2,3分别列出KCL方程:(设 流出取正) i1 + i 2 + iS2 + i4 – iS4 = 0 i3 + i 5 – i2 – iS2 = 0 i6 + iS6 – i1 – i 3 = 0 利用OL各电阻上的电流可以用节点电压表示为 i1 = G1( u1 – u 3 ), i 2 = G 2 ( u1 – u 2 ), i 3 = G 3 ( u 2 – u 3), i 4 = G4 u1, i 5 = G5 u 2, i 6 = G6 u 3 代入KCL方程,合并整理后得 节点( 1 ) ( G1 + G2 + G 4 ) u1 – G 2 u 2 – G1 u 3 = iS4 – iS2 节点( 2 ) – G 2 u1 + ( G 2 + G3 + G 5 ) u 2 – G 3 u 3 = iS2 节点( 3 ) – G1 u1 – G 3 u 2 + ( G1 + G3 + G 6 ) u 3 = - iS6 G11 G22 G33 G12 G13 G21 G23 G31 G32 (∑I S )1 (∑I S ) 2 (∑I S ) 3 第 2-20 页 前一页 下一页 返回本章目录 3、节点法方程的列写规律