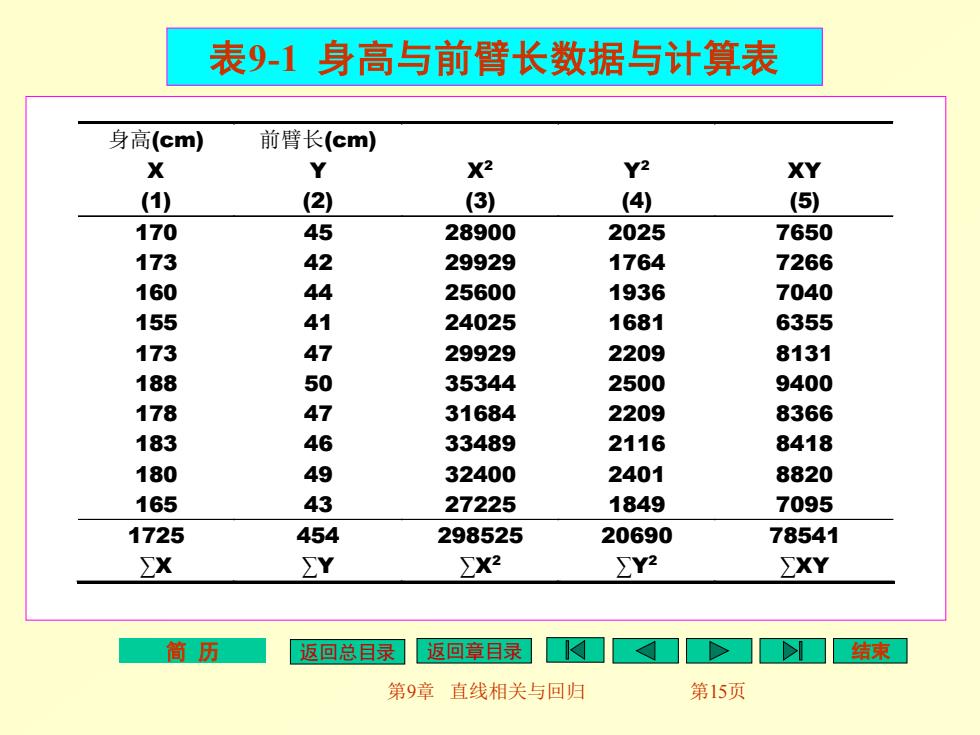
表9-1身高与前臂长数据与计算表 身高(cm) 前臂长(cm) X Y X2 Y2 XY (1) (2) (3) (4) (5) 170 45 28900 2025 7650 173 42 29929 1764 7266 160 44 25600 1936 7040 155 41 24025 1681 6355 173 47 29929 2209 8131 188 50 35344 2500 9400 178 47 31684 2209 8366 183 46 33489 2116 8418 180 49 32400 2401 8820 165 43 27225 1849 7095 1725 454 298525 20690 78541 ∑X ∑Y X2 Y2 ∑XY 简历 返回总目录 返回章目录 >i 结束 第9章直线相关与回归 第15页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第15页 表9-1 身高与前臂长数据与计算表 身高(cm) X 前臂长(cm) Y X2 Y2 XY (1) (2) (3) (4) (5) 170 45 28900 2025 7650 173 42 29929 1764 7266 160 44 25600 1936 7040 155 41 24025 1681 6355 173 47 29929 2209 8131 188 50 35344 2500 9400 178 47 31684 2209 8366 183 46 33489 2116 8418 180 49 32400 2401 8820 165 43 27225 1849 7095 1725 ∑X 454 ∑Y 298525 ∑X2 20690 ∑Y2 78541 ∑XY

(2)根据表9-1原始数据计算出∑X,∑Y,∑X2,∑Y2, ∑XY。 本例∑X=1725,∑Y=454, ∑X2=298525,∑Y2=20690,∑XY=78541. (3)计算X、Y的离均差平方和与离均差积和 m=ΣX2②X=298525- 7252 =962.5 n 10 n=r:_①)= 20690 4542 =78.4 n 10 筒历 返回总目录 返回章目录 第9章直线相关与回归 第16页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第16页 (2)根据表9-1原始数据计算出∑X,∑Y,∑X2 ,∑Y2 , ∑XY 。 本例∑X=1725,∑Y=454, ∑X2=298525,∑Y2=20690,∑XY=78541。 (3)计算X、Y的离均差平方和与离均差积和 962.5 10 1725 298525 ( ) 2 2 2 = − = = − n X l X X X 78.4 10 454 20690 ( ) 2 2 2 = − = = − n Y l YY Y
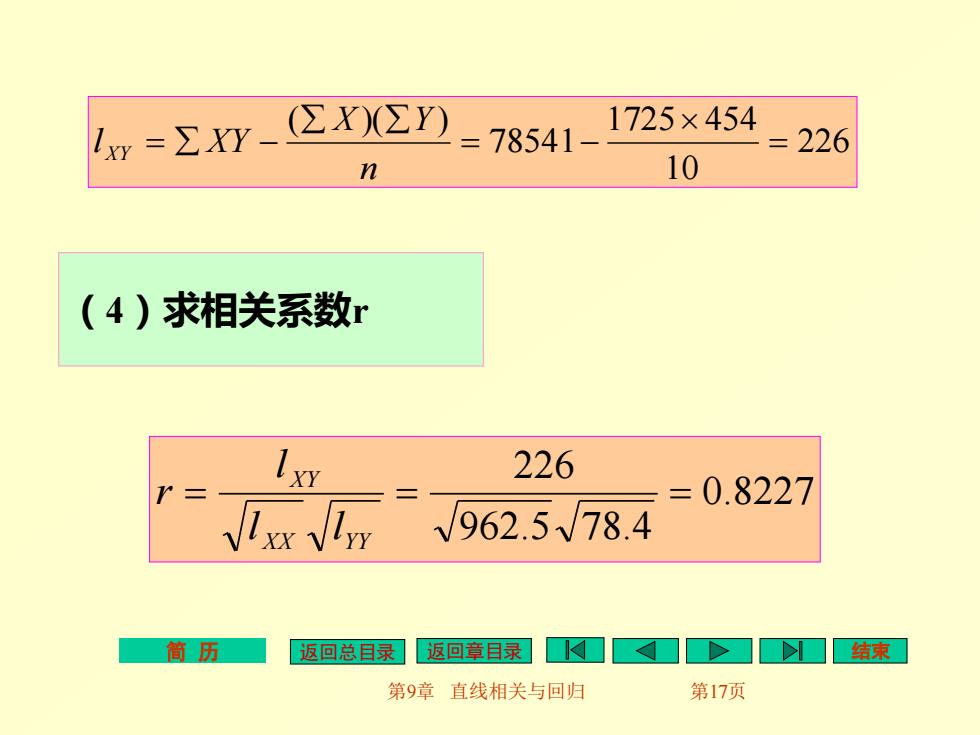
1w=ΣX灯-②2四 78541-1725x454 = 226 n 10 (4)求相关系数r 1 226 0.8227 √962.5√78.4 筒历 返回总目绿 返回章目录4口>口结束幻 第9章直线相关与回归 第17页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第17页 (4)求相关系数r 226 10 1725 454 78541 ( )( ) = = − = − n X Y l X Y XY 0.8227 962.5 78.4 226 = = = X X YY X Y l l l r
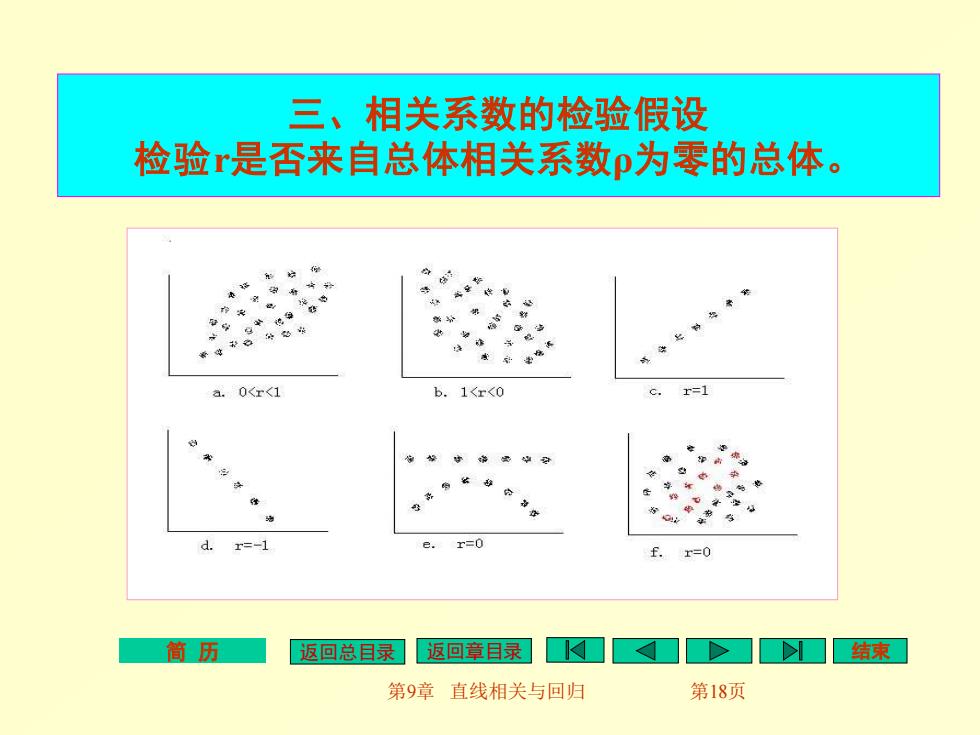
三、相关系数的检验假设 检验是否来自总体相关系数p为零的总体。 a a.0<r<1 b.1<r<0 x=1 5 d. r=-1 r=0 f. r=0 筒历 返回总目录返回章目录风口>]口结束 第9章直线相关与回归 第18页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第18页 三、相关系数的检验假设 检验r是否来自总体相关系数ρ为零的总体

1.t检验法1 检验的计算公式 S 一r2 简历 返回总目录 返回章目录口>口结束 第9章直线相关与回归 第19页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第19页 1. t 检验法 t检验的计算公式 r Sr r S r t | 0 | | | = − = 2 1 2 − − = n r Sr