
第2章ATLAB语言基础 21 无符号 uint32 uint64 整型 有符5 数值型 int64 单精度 基本型 浮点型 双精度 字符串型 数据类型 数组型 构造型 细胞型 结构型 米米刑 符号对象 图2.1 MATLAB的主要数据类型 有失严谨,会给搜索和确定一个符号是否为变量名带来更多的时间开销。在17.1节中曾经 指出过这一问题。 2.1.2常量与变量 常量是程序语句中取不变值的哪些量,如表达式y0.618x,其中就包含一个0.618这 样的数值常数,它便是一数值常量。而另一表达式s=Tomorrow and Tomorrow中,单引号 内的英文字符串“Tomorrow and Tomorrow”则是一字符串常量。 在MATLAB中,有一类常量是由系统默认给定一个符号来表示的,例如pi,它代表 圆周率π这个常数,即3.1415926,类似于C语言中的符号常量,这些常量如表2-1所列, 有时又称为系统预定义的变量 变量是在程序运行中其值可以改变的量,变量由变量名来表示。在MATLAB中变量 名的命名有自己的规则,可以归纳成如下几条: ()变最名必须以字母开头,且只能由字母、数字或者下画线3类符号组成,不能含 有空格和标点符号(如(),。%)等。 21
第 2 章 MATLAB 语言基础 ·21· ·21· 数据类型 基本型 数值型 字符串型 整 型 浮点型 有符号 int8 int16 int32 int64 单精度 双精度 构造型 符号对象 细胞型 结构型 类类型 uint64 数组型 无符号 uint16 uint32 uint8 图 2.1 MATLAB 的主要数据类型 有失严谨,会给搜索和确定一个符号是否为变量名带来更多的时间开销。在 1.7.1 节中曾经 指出过这一问题。 2.1.2 常量与变量 常量是程序语句中取不变值的哪些量,如表达式 y=0.618*x,其中就包含一个 0.618 这 样的数值常数,它便是一数值常量。而另一表达式 s='Tomorrow and Tomorrow'中,单引号 内的英文字符串“Tomorrow and Tomorrow”则是一字符串常量。 在 MATLAB 中,有一类常量是由系统默认给定一个符号来表示的,例如 pi,它代表 圆周率 π 这个常数,即 3.1415926…,类似于 C 语言中的符号常量,这些常量如表 2-1 所列, 有时又称为系统预定义的变量。 变量是在程序运行中其值可以改变的量,变量由变量名来表示。在 MATLAB 中变量 名的命名有自己的规则,可以归纳成如下几条: (1) 变量名必须以字母开头,且只能由字母、数字或者下画线 3 类符号组成,不能含 有空格和标点符号(如( ),。% ’)等

2 工,AB基础及其应用教程 表2-1 MATLAB特殊常量表 常量符号 常量含义 i或i 虚数单位,定义为2=2=-1 nr或inf 正无穷大,由零做除数引入此常量 NaN 不定式,表示非数值量,产生于00,0/,0°©等运算 pi 圆周率π的双精度表示 eps 容差变量,当某量的绝对值小于s时,可认为此量为零,即为浮点数的最小 ,PC上此值为2四 Realmin或realmin 最小浮点数,2 Realmax或realmax 最大浮点数,2@ 2)变量名区分字母的大小写。例如,“a”和“A”是不同的变量。 ()变量名不能超过63个字符,第63个字符后的字符被忽略,对于MATLAB6.5版 以前的变量名不能超过3引个字符 (4)关键字(如if、while等)不能作为变量名。 (⑤)最好不要用表2-1中的特殊常量符号作变量名。 常见的错误命名如x,y,y,A等。 2.1.3标量、向量、矩阵与数组 标量、向量、矩阵和数组是MATLAB运算中涉及的一组基木运算量。它们各自的特 点及相互间的关系可以描述如下: ()数组不是一个数学量,而是一个用于高级语言程序设计的概念。如果数组元素按 一维线性方式组织在一起,那么称其为一维数组, 一维数组的数学原型是向量。如果数组 元素分行、列排成 个二维平面表格,那么称其为二维数组 维数组的数学原型是矩阵 如果元素在排成二维数组的基础上,再将多个行、列数分别相同的二维数组叠成一本立 表格,便形成三维数组。依此类推下去,便有了多维数组的概念。在MATLAB中,数组 的用法与一般高级语言不同,它不借助于循环,而是直接采用运算符,有自己独立的运算 符和运算法则。2.15节和24节将有专门讨论 (2)矩阵是 个数学概 一般高级语言并未引入将其作为基本的运算量,但MATLAB 是个例外。 一般高级语言是不认可将两个矩阵视为两个简单变量而直接进行加减乘除的 要完成矩阵的四则运算必须借助于循环结构。当MATLAB将矩阵引入作为基本运算量后 上述局面改变了。MATLAB不仅实现了矩阵的简单加减乘除运算,而且许多与矩阵相关的 其他运算也因此大大简化了。 (3)向量是一个数学量 一般高级语言中也未引入,它可视为矩阵的特例.从MATLAB 的工作空间窗口可以查看到: 个n维的行向量是一个1×n阶的矩阵,而列向量则当成n× 阶的矩阵。 (4)标量的提法也是一个数学概念,但在MATLAB中,一方面可将其视为一般高级语 言的简单变量米处理,另一方面又可把它当成1×1阶的矩阵,这一看法与矩阵作为 2
·22· MATLAB 基础及其应用教程 ·22· 表 2-1 MATLAB 特殊常量表 常量符号 常量含义 i 或 j 虚数单位,定义为 2 2 ij 1 = = − Inf 或 inf 正无穷大,由零做除数引入此常量 NaN 不定式,表示非数值量,产生于 0/0,∞ /∞ ,0*∞ 等运算 pi 圆周率 π 的双精度表示 eps 容差变量,当某量的绝对值小于 eps 时,可认为此量为零,即为浮点数的最小 分辨率,PC 上此值为 2 -52 Realmin 或 realmin 最小浮点数,2 -1022 Realmax 或 realmax 最大浮点数,21023 (2) 变量名区分字母的大小写。例如,“a”和“A”是不同的变量。 (3) 变量名不能超过 63 个字符,第 63 个字符后的字符被忽略,对于 MATLAB 6.5 版 以前的变量名不能超过 31 个字符。 (4) 关键字(如 if、while 等)不能作为变量名。 (5) 最好不要用表 2-1 中的特殊常量符号作变量名。 常见的错误命名如 f(x),y',y'',A2 等。 2.1.3 标量、向量、矩阵与数组 标量、向量、矩阵和数组是 MATLAB 运算中涉及的一组基本运算量。它们各自的特 点及相互间的关系可以描述如下: (1) 数组不是一个数学量,而是一个用于高级语言程序设计的概念。如果数组元素按 一维线性方式组织在一起,那么称其为一维数组,一维数组的数学原型是向量。如果数组 元素分行、列排成一个二维平面表格,那么称其为二维数组,二维数组的数学原型是矩阵。 如果元素在排成二维数组的基础上,再将多个行、列数分别相同的二维数组叠成一本立体 表格,便形成三维数组。依此类推下去,便有了多维数组的概念。在 MATLAB 中,数组 的用法与一般高级语言不同,它不借助于循环,而是直接采用运算符,有自己独立的运算 符和运算法则,2.1.5 节和 2.4 节将有专门讨论。 (2) 矩阵是一个数学概念,一般高级语言并未引入将其作为基本的运算量,但 MATLAB 是个例外。一般高级语言是不认可将两个矩阵视为两个简单变量而直接进行加减乘除的, 要完成矩阵的四则运算必须借助于循环结构。当 MATLAB 将矩阵引入作为基本运算量后, 上述局面改变了。MATLAB 不仅实现了矩阵的简单加减乘除运算,而且许多与矩阵相关的 其他运算也因此大大简化了。 (3) 向量是一个数学量,一般高级语言中也未引入,它可视为矩阵的特例。从 MATLAB 的工作空间窗口可以查看到:一个 n 维的行向量是一个 1×n 阶的矩阵,而列向量则当成 n×1 阶的矩阵。 (4) 标量的提法也是一个数学概念,但在 MATLAB 中,一方面可将其视为一般高级语 言的简单变量来处理,另一方面又可把它当成 1×1 阶的矩阵,这一看法与矩阵作为
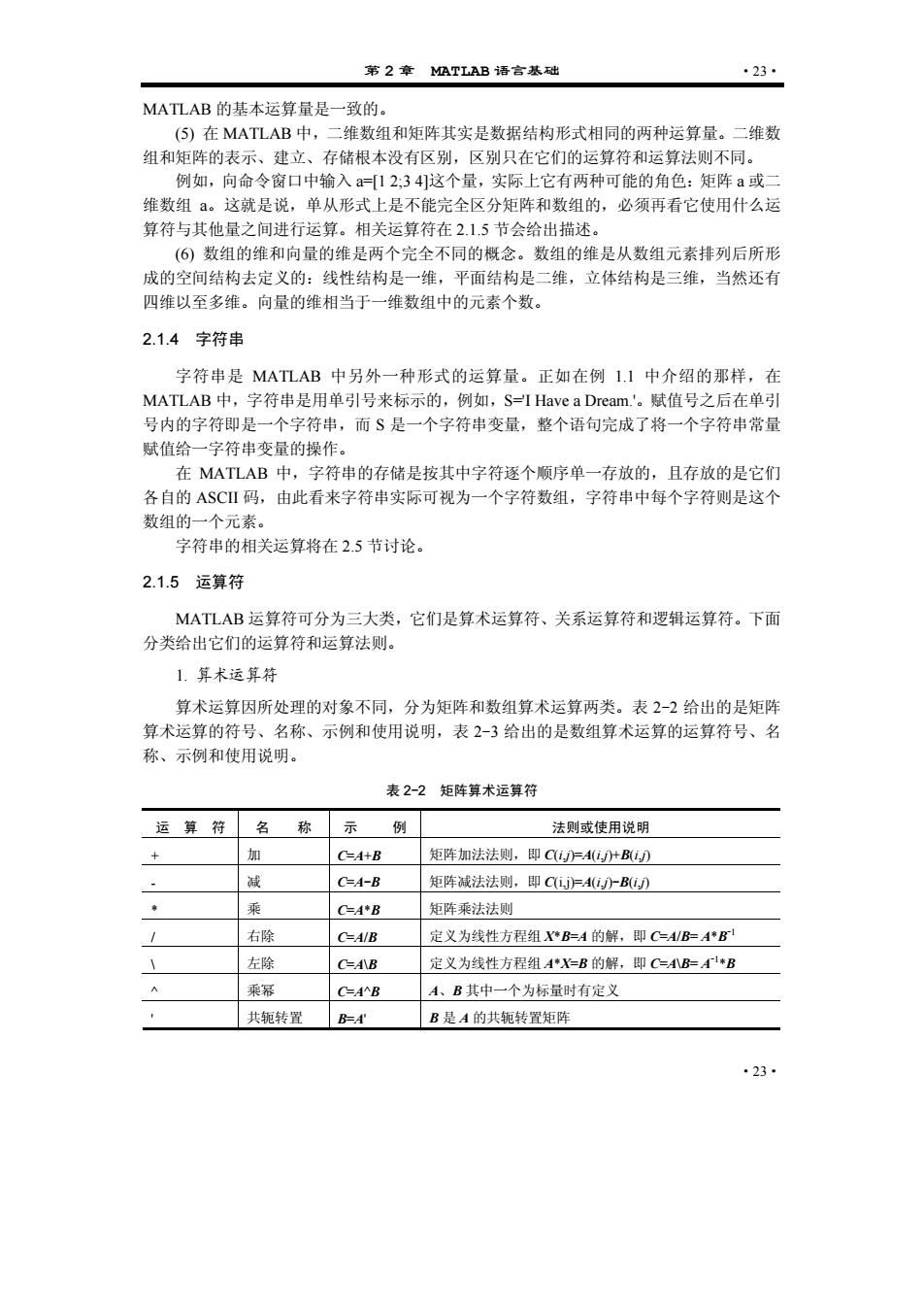
第2章MATLAB语言基础 .23 MATLAB的基本运算量是一致的 (⑤)在MATLAB中,二维数组和矩阵其实是数据结构形式相同的两种运算量。二维数 组和矩阵的表示、建立、存储根本没有区别,区别只在它们的运算符和运算法则不同。 例如,向命令窗口中输入a12:34这个最,实际上它有两种可能的角色:矩阵a或二 维数组ā。这就是说,单从形式上是不能完全区分矩阵和数组的,必须再看它使用什么运 算符与其他量之间进行运算。相关运算符在2.1.5节会给出描述 (⑥)数组的维和向最的维是两个完全不同的概念。数组的维是从数组元素排列后所形 成的空间结构去定义的:线性结构是一维,平面结构是二维,立体结构是三维,当然还有 四维以至多维。向量的维相当于一维数组中的元素个数。 2.14字符串 字符串是MATLAB中另外一种形式的运算最。正如在例1.1中介绍的那样,在 MATLAB中,字符串是用单引号来标示的,例如,S-I Have a Dream,'。赋值号之后在单引 号内的字符即是一个字符串,而S是一个字符串变量,整个语句完成了将一个字符串常量 情值给一字符串变量的操作】 在MATLAB中,字符串的存储是按其中字符逐个顺序单一存放的,且存放的是它们 各自的ASC码,由此看米字符串实际可视为一个字符数组,字符串中每个字符则是这个 数组的一个元素。 字符串的相关运算将在2.5节讨论。 2.1.5运算符 MATLAB运算符可分为 三大类,它们是算术运算符、关系运算符和逻辑运算符。下面 分类给出它们的运算符和运算法则。 1.算术运算符 算术运算因所处理的对象不同,分为矩阵和数组算术运算两类 表2-2给出的是矩阵 算术运算的符号、名称、示例和使用说明,表2-3给出的是数组算术运算的运算符号、名 称、示例和使用说明。 表2-2矩阵算术运算符 运算符 名 称 示 例 法则或使用说明 加 CA+B 矩阵加法法则,即CUFA(肚BD C=A-B 柜阵减法法则,即C小B 乘 C'B 矩阵乘法法则 右除 C-AIB 定义为线性方程组XB=4的解,即C=4/B=A*B C=A\B 定义为线性方程组AXB的解,即CB=B 垂某 CAB A、B其中一个为标量时有定义 共轭转置 B是A的共矩转置矩阵 23
第 2 章 MATLAB 语言基础 ·23· ·23· MATLAB 的基本运算量是一致的。 (5) 在 MATLAB 中,二维数组和矩阵其实是数据结构形式相同的两种运算量。二维数 组和矩阵的表示、建立、存储根本没有区别,区别只在它们的运算符和运算法则不同。 例如,向命令窗口中输入 a=[1 2;3 4]这个量,实际上它有两种可能的角色:矩阵 a 或二 维数组 a。这就是说,单从形式上是不能完全区分矩阵和数组的,必须再看它使用什么运 算符与其他量之间进行运算。相关运算符在 2.1.5 节会给出描述。 (6) 数组的维和向量的维是两个完全不同的概念。数组的维是从数组元素排列后所形 成的空间结构去定义的:线性结构是一维,平面结构是二维,立体结构是三维,当然还有 四维以至多维。向量的维相当于一维数组中的元素个数。 2.1.4 字符串 字符串是 MATLAB 中另外一种形式的运算量。正如在例 1.1 中介绍的那样,在 MATLAB 中,字符串是用单引号来标示的,例如,S='I Have a Dream.'。赋值号之后在单引 号内的字符即是一个字符串,而 S 是一个字符串变量,整个语句完成了将一个字符串常量 赋值给一字符串变量的操作。 在 MATLAB 中,字符串的存储是按其中字符逐个顺序单一存放的,且存放的是它们 各自的 ASCII 码,由此看来字符串实际可视为一个字符数组,字符串中每个字符则是这个 数组的一个元素。 字符串的相关运算将在 2.5 节讨论。 2.1.5 运算符 MATLAB 运算符可分为三大类,它们是算术运算符、关系运算符和逻辑运算符。下面 分类给出它们的运算符和运算法则。 1. 算术运算符 算术运算因所处理的对象不同,分为矩阵和数组算术运算两类。表 2-2 给出的是矩阵 算术运算的符号、名称、示例和使用说明,表 2-3 给出的是数组算术运算的运算符号、名 称、示例和使用说明。 表 2-2 矩阵算术运算符 运 算 符 名 称 示 例 法则或使用说明 + 加 C=A+B 矩阵加法法则,即 C(i,j)=A(i,j)+B(i,j) - 减 C=A-B 矩阵减法法则,即 C(i,j)=A(i,j)-B(i,j) * 乘 C=A*B 矩阵乘法法则 / 右除 C=A/B 定义为线性方程组 X*B=A 的解,即 C=A/B= A*B-1 \ 左除 C=A\B 定义为线性方程组 A*X=B 的解,即 C=A\B= A-1 *B ^ 乘幂 C=A^B A、B 其中一个为标量时有定义 ' 共轭转置 B=A' B 是 A 的共轭转置矩阵

·24. 工AB基础及其应用教程 表2-3数组算术运算符 运算符名称 示 法则或使用说明 数组乘 C=4.*B CijA(ijyB(i) 数组右险=4B CYiM=A(iBin 数组左除C-4B Clif)=BiJA(ij) 数组乘幂C=4AB CineA(iB(n 转置 将数组的行摆放成列,复数元素不做共轭 针对表2-2和表2-3需要说明儿点: (口)矩阵的加减、乘运算是严格按矩阵运算法则定义的,而矩阵的除法虽和矩阵求逆 有关系,但却分了左、右除,因此不是完全等价的。乘幂运算更是将标量幂扩展到矩阵可 作为票指数。总的来说,MATLAB接受了线性代数已有的矩阵坛算规则,但又不仅止于此 麦义中先未定义数组的加诚祛,是为施降的减林与黄超的减越肌. (3)不论是加减乘除,还是乘幂,数组的运算都是元素间的运算,即对应下标元素一 对一的运算。 (④多维数组的运算法则,可依元素按下标一一对应参与运算的原则将表2-3推广。 2.关系运算特 MATLAB关系运算符列在表2-4中. 表2-4关系运算符 运算符名称示例 法则或使用说明 小于 A<B 1.小B都是标量,结果是或为1真)减为假的标量 小于等于AB 与 数组各元素逐 大于 比牧,结果为与运算数组行列相同的数组,其中各元素取值 A>B 或1或0 大于等于AP=B 3,A、B均为数组时,必须行、列数分别相同,A与B各对应 相等于 A=B 素相比较,结果为与A或B行列相同的数组,其中各元素取值 或1或0 不等于 d~=B 4.==和一=运算对参与比较的量同时比较实部和虚部,其他运 算只比较实部 需要明确指出的是,MATLAB的关系运算可看成矩阵的关系运算,但严格地讲,把 关系运算 础之 。因为从 2一 所列法则不 发现 系起 值是 素一对一的运算结果。数组的关系运算向下可兼容一般高级语言中所定义的标量关系运算 3.逻辑运算符 逻辑运算在MATLAB中同样需要,为此MATLAB定义了自己的逻辑运算符,并设定 了相应的逻辑运算法则,如表2-5所示。 24
·24· MATLAB 基础及其应用教程 ·24· 表 2-3 数组算术运算符 运算符 名 称 示 例 法则或使用说明 .* 数组乘 C=A.*B C(i,j)=A(i,j)*B(i,j) ./ 数组右除 C=A./B C(i,j)=A(i,j)/B(i,j) .\ 数组左除 C=A.\B C(i,j)=B(i,j)/A(i,j) .^ 数组乘幂 C=A.^B C(i,j)=A(i,j)^B(i,j) .' 转置 A.' 将数组的行摆放成列,复数元素不做共轭 针对表 2-2 和表 2-3 需要说明几点: (1) 矩阵的加减、乘运算是严格按矩阵运算法则定义的,而矩阵的除法虽和矩阵求逆 有关系,但却分了左、右除,因此不是完全等价的。乘幂运算更是将标量幂扩展到矩阵可 作为幂指数。总的来说,MATLAB 接受了线性代数已有的矩阵运算规则,但又不仅止于此。 (2) 表 2-3 中并未定义数组的加减法,是因为矩阵的加减法与数组的加减法相同,所 以未做重复定义。 (3) 不论是加减乘除,还是乘幂,数组的运算都是元素间的运算,即对应下标元素一 对一的运算。 (4) 多维数组的运算法则,可依元素按下标一一对应参与运算的原则将表 2-3 推广。 2. 关系运算符 MATLAB 关系运算符列在表 2-4 中。 表 2-4 关系运算符 运算符 名 称 示 例 法则或使用说明 < 小于 A<B <= 小于等于 A<=B > 大于 A>B >= 大于等于 A>=B == 恒等于 A==B ~= 不等于 A~=B 1.A、B 都是标量,结果是或为 1(真)或为 0(假)的标量 2.A、B 若一个为标量,另一个为数组,标量将与数组各元素逐 一比较,结果为与运算数组行列相同的数组,其中各元素取值 或 1 或 0 3.A、B 均为数组时,必须行、列数分别相同,A 与 B 各对应元 素相比较,结果为与 A 或 B 行列相同的数组,其中各元素取值 或 1 或 0 4.==和~=运算对参与比较的量同时比较实部和虚部,其他运 算只比较实部 需要明确指出的是,MATLAB 的关系运算虽可看成矩阵的关系运算,但严格地讲,把 关系运算定义在数组基础之上更为合理。因为从表 2-4 所列法则不难发现,关系运算是元 素一对一的运算结果。数组的关系运算向下可兼容一般高级语言中所定义的标量关系运算。 3. 逻辑运算符 逻辑运算在 MATLAB 中同样需要,为此 MATLAB 定义了自己的逻辑运算符,并设定 了相应的逻辑运算法则,如表 2-5 所示

第2章ATLAB语言基础 .25 表2-5逻辑运算符 运算符名称示例 法则或使用说明 与 4&B 1.小、B都为标量,结果是或为1(真)或为0假)的标量 2,A、B若一个为标量,另一个为数组,标量将与数组各元素逐 或 一做逻辑运算,结果为与运算数组行列相同的数组,其中各元素 取值或1或 非 A 3.小、B均为数组时,必须行、列数分别相同,A与B各对应元素 && 先决与 A&&B 做逻辑运算,结果为与A或B行列相同的数组,其中各元素取值 成1或0 先决或AB 4。先决与、。先决或是只针对标量的运算 同样地,MATLAB的逻辑运算也是定义在数组的基础之上,向下可兼容一般高级语言 中所定义的标量逻辑运算 为提高运算速度,MATLAB还定义了针对标量的先决与和先决或运算。先决与运算是 当该运算符的左边为1(真)时,才继续与该符号右边的量做逻辑运算。先决或运算是当运算 符的左边为1(真)时,就不需要继续与该符号右边的量做逻辑运算,而立即得出该逻辑运算 结果为1(真):否则,就要继续与该符号右边的量运算。 4.运算符的优先级 和其他高级语言一样,当用多个运算符和运算量写出一个MATLAB表达式时,运算 符的优先次序是一个必须明确的问题。表2-6列出了运算符的优先次序。 表26 MATLAB运算符的优先次序 优先次序 运算符 最高转置共轭)、矩阵乘幂、:《转置、(数组乘幂) 一(逻辑非) ·、右除)、左除)、*(数组乘)、数组右除)、(数组左除) +、 :(目号运算 <,=,>.,恒等于不等于) &(逻辑与) 逻组或) &(先决与) 最低先决或 MATLAB运算符的优先次序在表26中依从上到下的顺序,分别由高到低。而表中同 ·25
第 2 章 MATLAB 语言基础 ·25· ·25· 表 2-5 逻辑运算符 运算符 名 称 示 例 法则或使用说明 & 与 A&B | 或 A|B ~ 非 ~A && 先决与 A&&B || 先决或 A||B 1.A、B 都为标量,结果是或为 1(真)或为 0(假)的标量 2.A、B 若一个为标量,另一个为数组,标量将与数组各元素逐 一做逻辑运算,结果为与运算数组行列相同的数组,其中各元素 取值或 1 或 0 3.A、B 均为数组时,必须行、列数分别相同,A 与 B 各对应元素 做逻辑运算,结果为与 A 或 B 行列相同的数组,其中各元素取值 或 1 或 0 4.先决与、先决或是只针对标量的运算 同样地,MATLAB 的逻辑运算也是定义在数组的基础之上,向下可兼容一般高级语言 中所定义的标量逻辑运算。 为提高运算速度,MATLAB 还定义了针对标量的先决与和先决或运算。先决与运算是 当该运算符的左边为 1(真)时,才继续与该符号右边的量做逻辑运算。先决或运算是当运算 符的左边为 1(真)时,就不需要继续与该符号右边的量做逻辑运算,而立即得出该逻辑运算 结果为 1(真);否则,就要继续与该符号右边的量运算。 4. 运算符的优先级 和其他高级语言一样,当用多个运算符和运算量写出一个 MATLAB 表达式时,运算 符的优先次序是一个必须明确的问题。表 2-6 列出了运算符的优先次序。 表 2-6 MATLAB 运算符的优先次序 优先次序 运 算 符 最 高 '(转置共轭)、^(矩阵乘幂)、.'(转置)、.^(数组乘幂) ~(逻辑非) * 、/(右除)、\(左除)、.*(数组乘)、./(数组右除)、.\(数组左除) +、- :(冒号运算) <、<=、>、>=、==(恒等于)、~=(不等于) &(逻辑与) |(逻辑或) &&(先决与) 最 低 ||(先决或) MATLAB 运算符的优先次序在表 2-6 中依从上到下的顺序,分别由高到低。而表中同