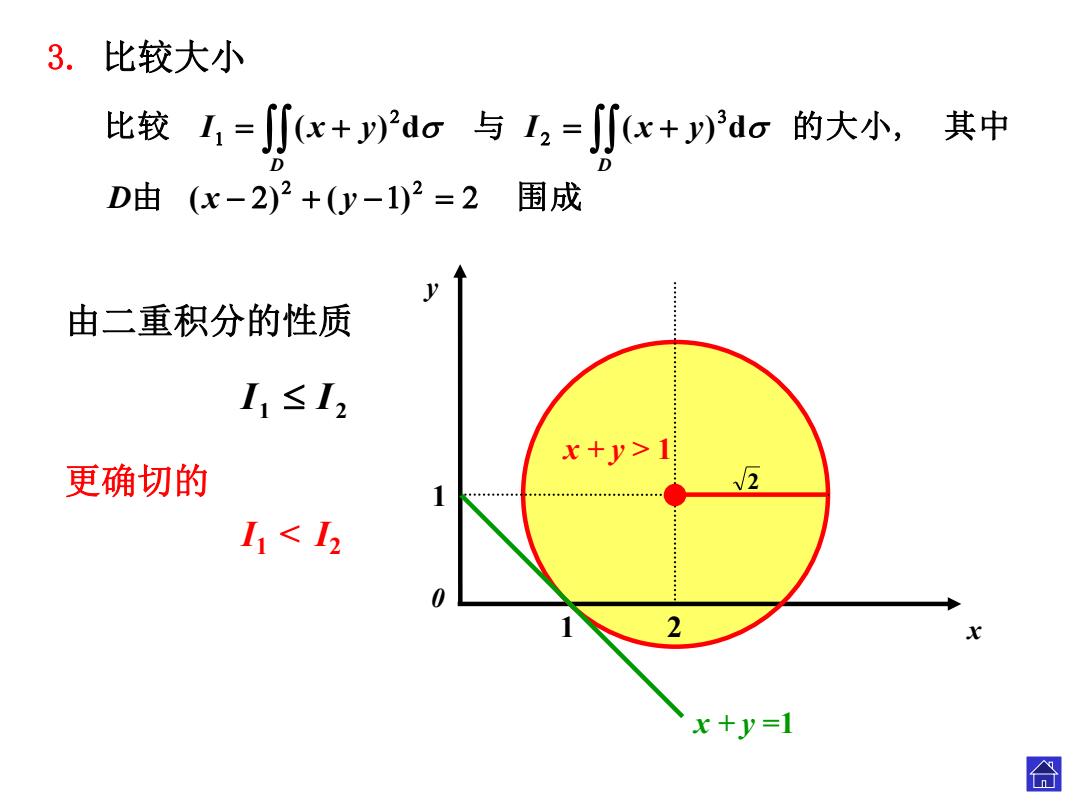
3.比较大小 比较1,=∬x+Pdo与1,=∬x+3do的大小, 其中 D由(x-2)2+(y-1)2=2围成 y 由二重积分的性质 I1≤I2 x+y>1 更确切的 I1<12 0 2 x+y=1 合
0 y x 1 1 2 x + y =1 2 x + y > 1 由 围 成 比 较 与 的大小, 其 中 ( ) ( ) ( ) d ( ) d D x y I x y I x y D D 1 2 I I 由二重积分的性质 更确切的 I1 < I2 3. 比较大小
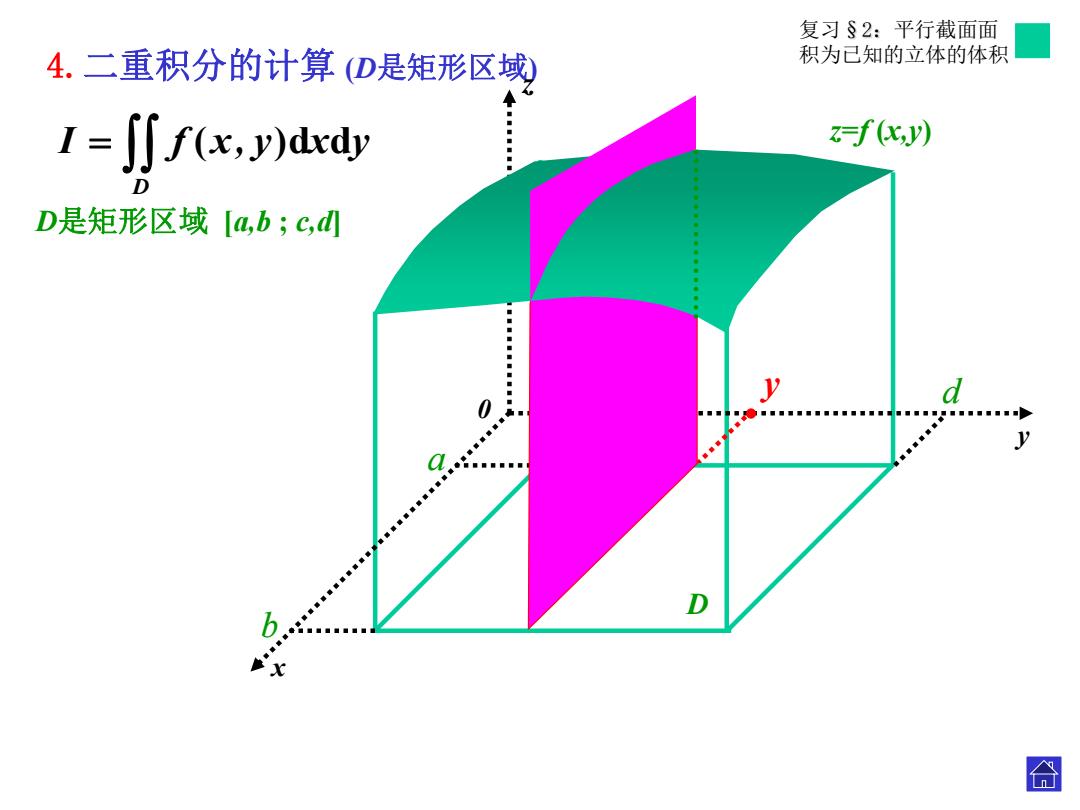
复习§2:平行截面面 4.二重积分的计算(D是矩形区域, 积为已知的立体的体积 I=J∬f(x,y)ddy f化,) ◆ D是矩形区域[a,b;c,d 0 d y D b 合
4.二重积分的计算 (D是矩形区域) 复习§2:平行截面面 积为已知的立体的体积 y 0 x z y a b c d D D是矩形区域 [a,b ; c,d] z=f (x,y) D I f (x, y)dxdy

4.二重积分的计算(D是矩形区域) z=f(x,y) y=y I=J∬f(x,y)ddw f(x,y) ◆ D是矩形区域[a,b;c,d 0y)=∫f(x,y)dx I =f"e(y)dr a 0 b 问题: Q(y)是什么图形?是曲边梯形
y 0 x z y a b c d D D是矩形区域 [a,b ; c,d] z=f (x,y) b a f (x, y)dx Q( y) y y z f (x, y) 问题:Q( y)是什么图形? Q( y ) = 是曲边梯形。 D I f (x, y)dxdy . 4. 二重积分的计算 (D是矩形区域) . d c I Q( y)dy
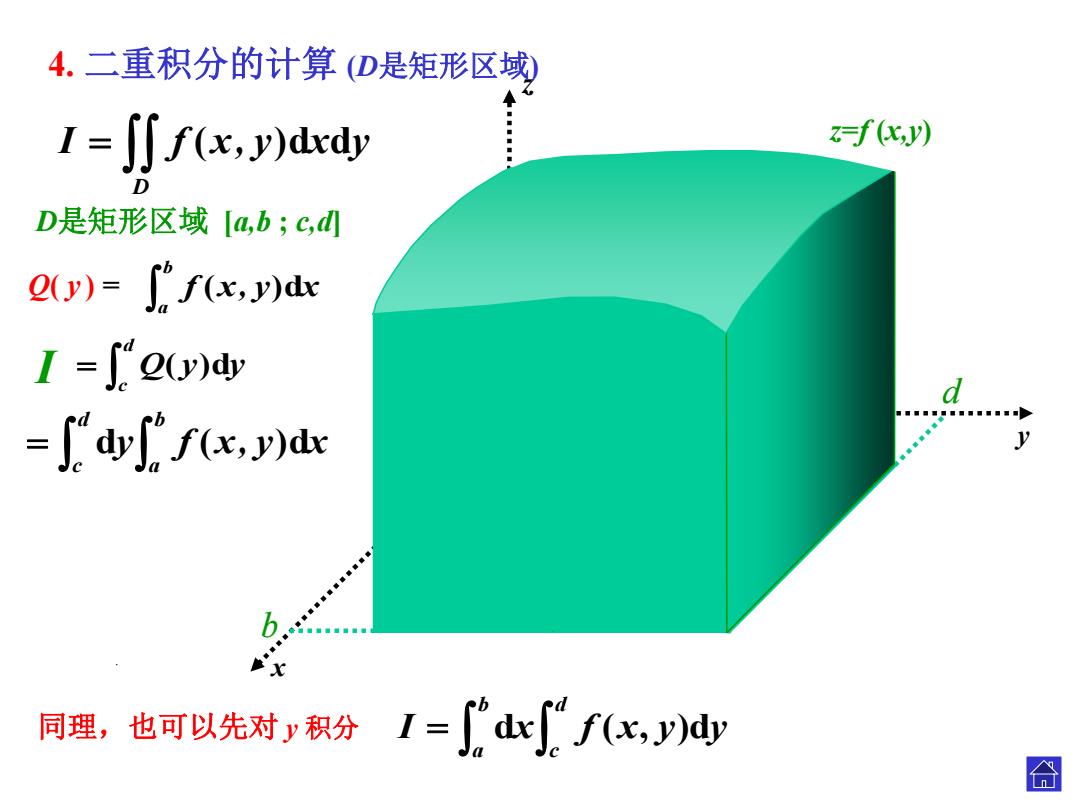
4.二重积分的计算(D是矩形区域) I=J∬f(x,y)ddy f化) ◆ D是矩形区域[a,b;c,d (y)=∫fx,y)de I =["Q(y)dy d -Sdyff(x.y)dx y b 同理,也可以先对y积分I=dxf(x,y)d 合
0 x z y y a b c d D d c b a dy f (x, y)dx . b a Q( y ) = f (x, y)dx d c I Q( y)dy 同理,也可以先对 y 积分 b a d c I dx f (x, y)dy . . D I f (x, y)dxdy z=f (x,y) D是矩形区域 [a,b ; c,d] 4. 二重积分的计算 (D是矩形区域)
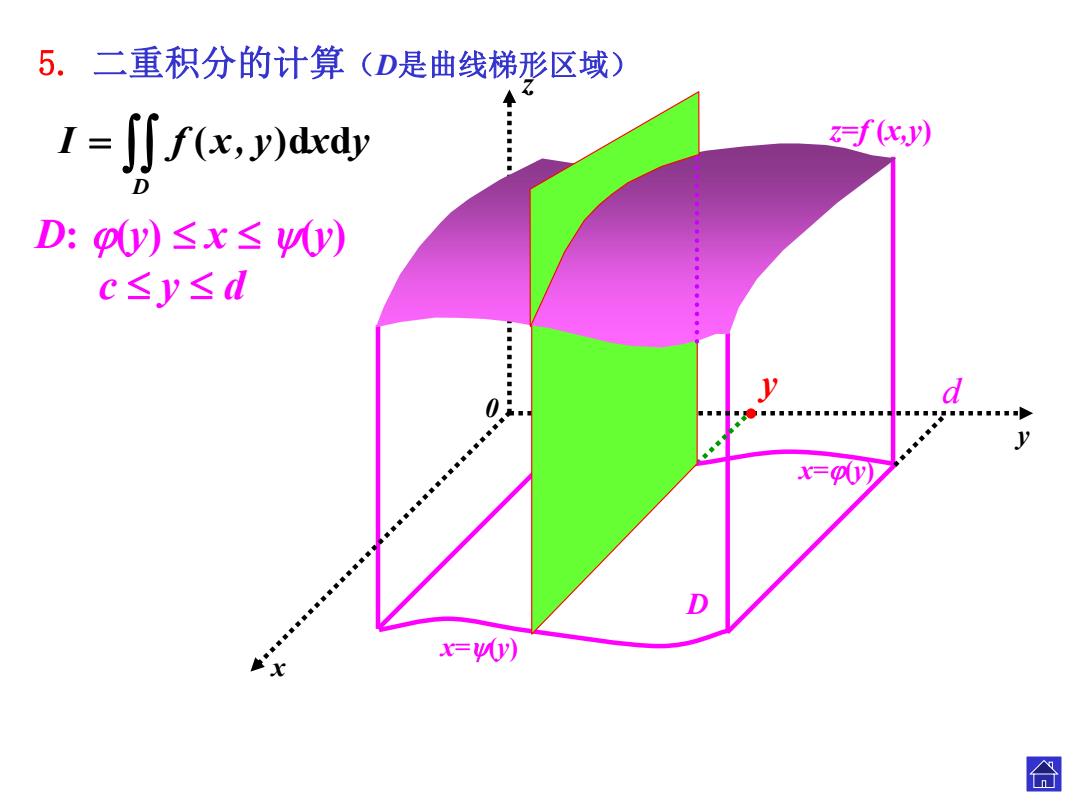
5.二重积分的计算(D是曲线梯形区域) I=f(x,y)dxdy f(化y) D:o0y)≤x≤0y) c≤y≤d 0 ◆ y X=) =0y) 合
0 x z y c d D z=f (x,y) x=(y) x=(y) y D: (y) x (y) c y d 5. 二重积分的计算(D是曲线梯形区域) D I f (x, y)dxdy