银川能源学院：《高等数学》课程教学资源（知识点课件讲稿）二重积分

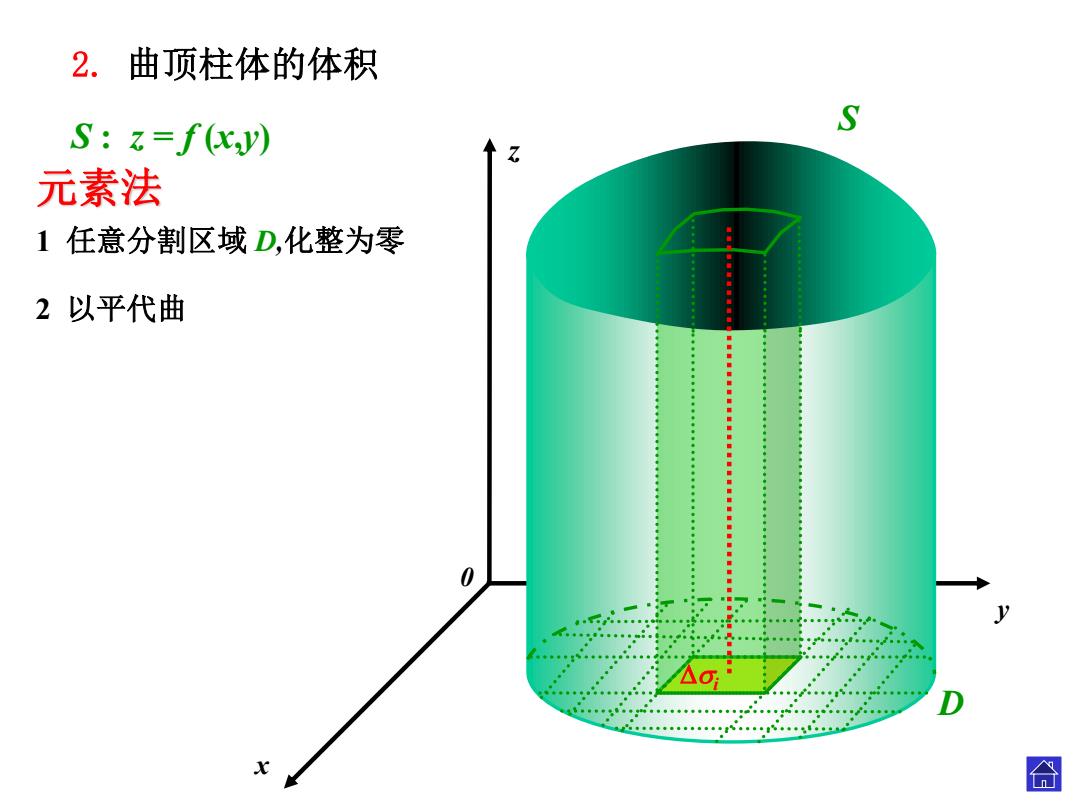
2.曲顶柱体的体积 S:z=f(xy) S 元素法 1任意分割区域D,化整为零 2以平代曲 0 合

x 0 z y D S S : z = f (x,y) 元素法 1 任意分割区域 D,化整为零 2 以平代曲 2. 曲顶柱体的体积 i

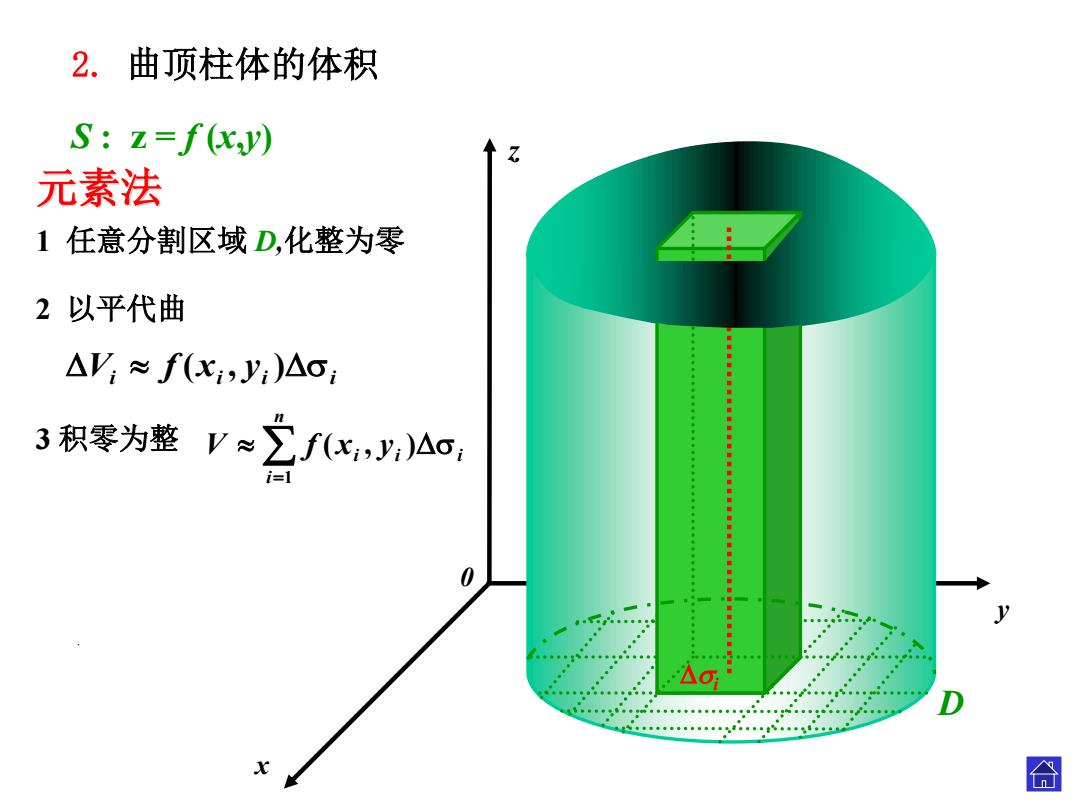
2.曲顶柱体的体积 S:z=f(xy) 元素法 1任意分割区域D,化整为零 2以平代曲 △V:≈f(x,y:)△o: 3积零为整V≈∑fx,,)ao, 0 △ 合

x 0 z y D S : z = f (x,y) i i i i V  f (x , y ) 3 积零为整    n i i i i V f x y 1 ( , ) 2 以平代曲 元素法 1 任意分割区域 D,化整为零 2. 曲顶柱体的体积 . i

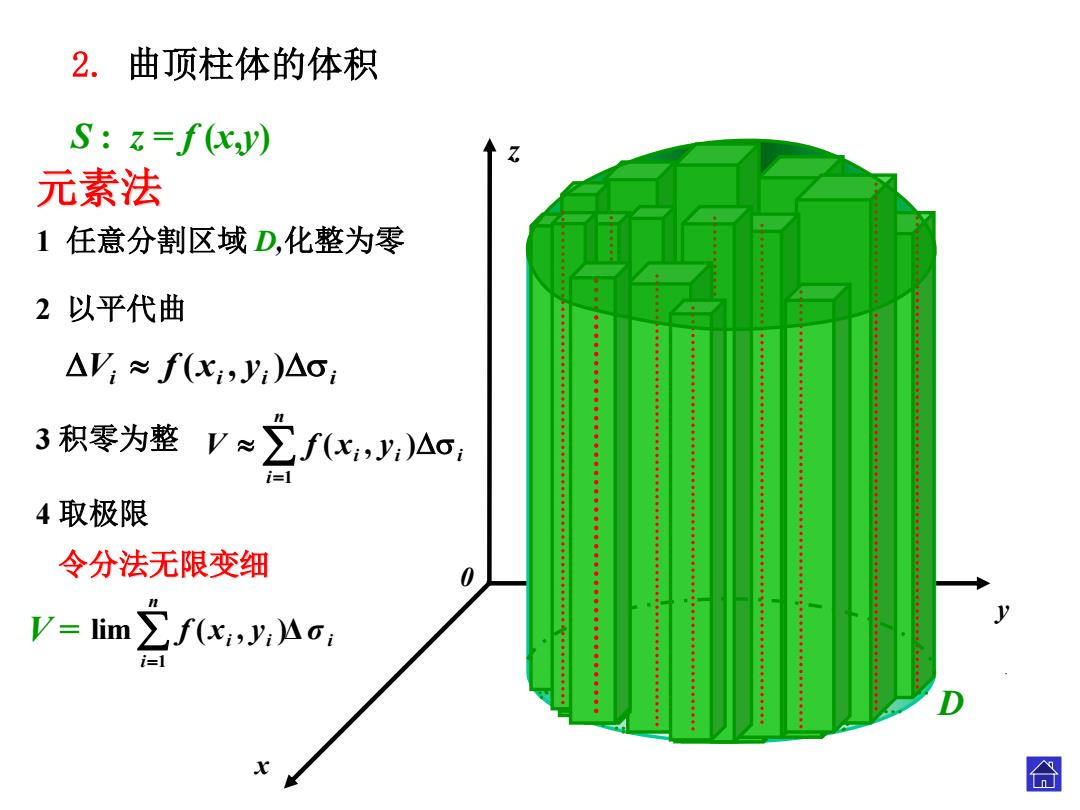
2.曲顶柱体的体积 S:z=f(xy) 元素法 1任意分割区域D,化整为零 2以平代曲 △V;≈f(x,y:)△o: 3积零为整V≈∑fxy,4o； 4取极限 令分法无限变细 0 V=im∑fx,y,Ao； i- 合

x 0 z y D S : z = f (x ,y ) i i i i  V  f ( x , y )  3 积零为整     n i i i i V f x y 1 ( , ) 4 取极限 令分法无限变细  i 2 以平代曲 元素法 1 任意分割区域 D,化整为零 2. 曲顶柱体的体积 . ni i i σ i f x y 1 V = lim ( , )Δ

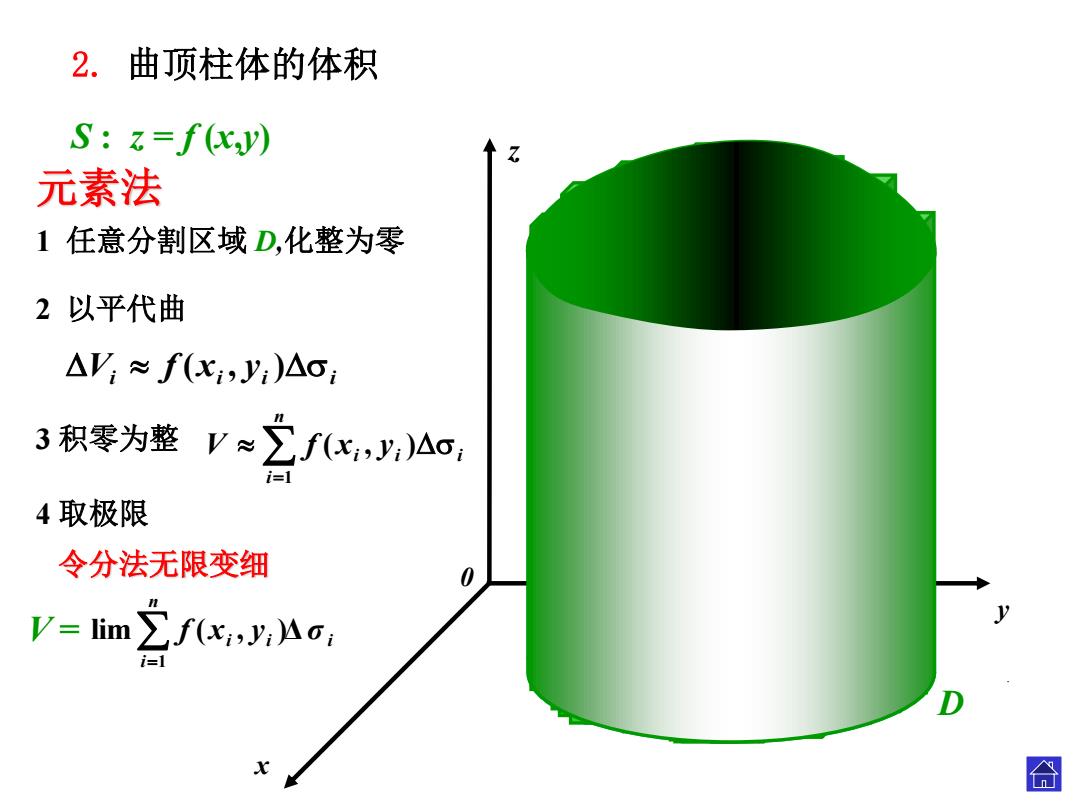
2.曲顶柱体的体积 S:z=f(xy) 元素法 1任意分割区域D,化整为零 2以平代曲 △V≈f(xy:)△o: 3积零为整V≈∑fx,,Ac 4取极限 令分法无限变细 0 V=lim∑fxy,Ao; 合

x 0 z y D S : z = f (x ,y ) i i i i  V  f ( x , y )  3 积零为整 i    ni i i i V f x y 1 ( , ) 4 取极限 令分法无限变细 2 以平代曲 元素法 1 任意分割区域 D,化整为零 2. 曲顶柱体的体积 . ni i i σ i f x y 1 V = lim ( , )Δ

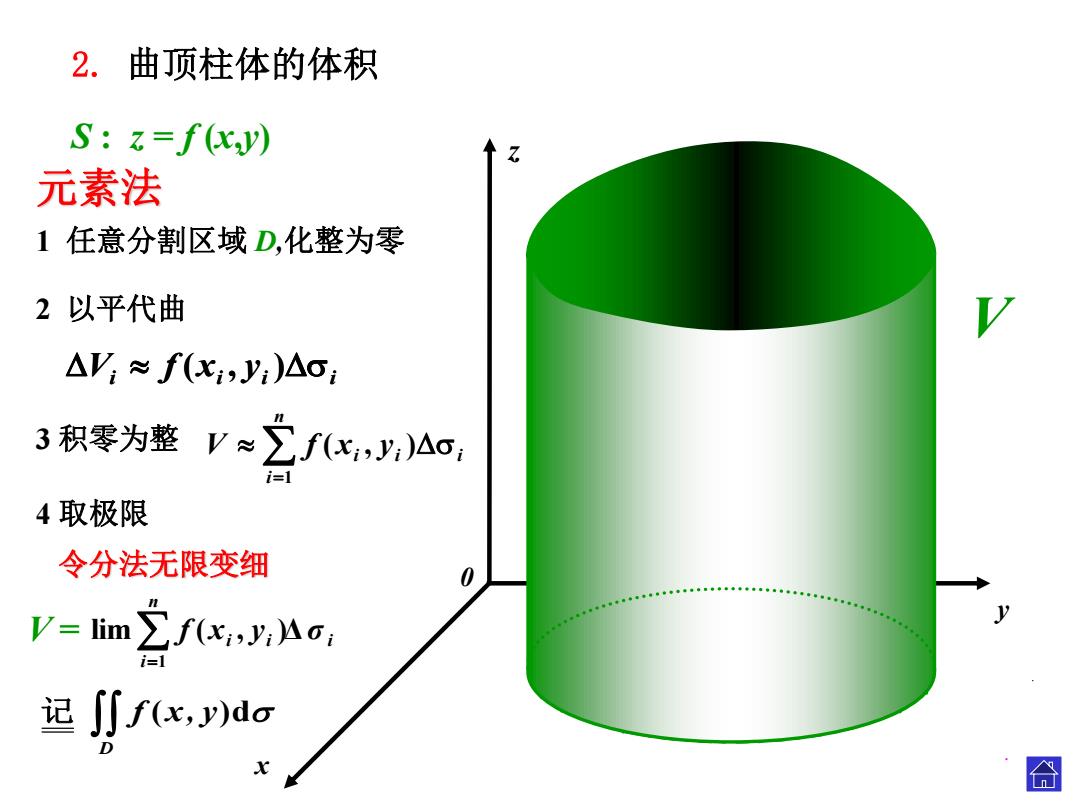
2.曲顶柱体的体积 S:z=f(xy) 元素法 1任意分割区域D,化整为零 2以平代曲 △V≈f(x,y)△o: 3积零为整V≈∑fx,,Ac 4取极限 令分法无限变细 0 V=lim∑fx,y,Aa, 记Jjf(x,y)do 囧

x 0 z y S : z = f (x ,y ) i i i i  Vi  f ( x i , y i )  i  V  f ( x , y )  3 积零为整 4 取极限f (x, y)d D  记 令分法无限变细 2 以平代曲 V 元素法 1 任意分割区域 D,化整为零 . 2. 曲顶柱体的体积 . ni i i σ i f x y 1 V = lim ( , )Δ     n i i i i V f x y 1 ( , )