
§2- 一元函数积分学
§2 一元函数积分学
主目 录(1-25)》 1曲边梯形的面积 2求曲线y2=2x与y=x-4围成的面积 3 求抛物线y=-x2+4x-3与其在点(0,-3)和点(3,0)处的切线所围 成图形的面积 4 曲边扇形的面积 5 旋轮线 6 旋轮线也叫摆线 7 旋轮线是最速降线 8 心形线 9星形线 10 圆的渐伸线 11笛卡儿叶形线 12 双纽线 13 阿基米德螺线 14 双曲螺线 15 求曲线r=3Cos0及r=1+cos0分别所围成的图形的公共部分的 面积 16 求曲线r=√2sin0及r2=cos20分别所围成的图形的公共部分的面 积
5 旋轮线 6 旋轮线也叫摆线 7 旋轮线是最速降线 8 心形线 9 星形线 10 圆的渐伸线 11 笛卡儿叶形线 12 双纽线 13 阿基米德螺线 14 双曲螺线 主 目 录(1–25 ) 15 16 面积 求曲线 r 3cosθ 及 r 1 cos θ 分别所围成的图形的公共部分的 积 求曲线 r 2sinθ 及 r 2 cos2 θ 分别所围成的图形的 公共部分的面 2 求曲线 2 与 4 围成的面积 2 y x y x 3 成图形的面积 求抛物线 y x 2 4x 3 与其在点(0,3)和点(3,0)处的 切线所围 1 曲边梯形的面积 4 曲边扇形的面积

17圆p≤1被心形线p=1+cos0分割为两部分,求这两部分的面积。 18 求由双纽线(x2+y2)2=a2(x2-y2)所围而且在圆周x2+y2= 2 内部的面积。 19平行截面面积为己知的立体的体积。 20半径为R的正圆柱体被通过其底的直径并与底面成a角的平面所截,得 一圆柱楔。求其体积。 21求以半径为R的圆为底,平行且等于底圆直径的线段为顶,高为的正 劈锥体的体积。■ 22旋转体体积(y=f(x)绕x轴) 23旋转体体积(x=g(6y)绕轴)■ 24旋转体体积(柱壳法) 25旋转体的侧面积 ■
19 平行截面面积为已知的立体的体积。 20 半径为R的正圆柱体被通过其底的直径并与底面成角的平面所截,得 一圆柱楔。求其体积。 21 求以半径为R的圆为底,平行且等于底圆直径的线段为顶,高为h的正 劈锥体的体积。 22 旋转体体积(y =f(x)绕x轴) 23 旋转体体积(x =g(y)绕y轴) 24 旋转体体积(柱壳法) 25 旋转体的侧面积 18 17 圆ρ 1被心形线 ρ 1 cosθ 分割为两部分,求这两 部分的面积。 求由双纽线 ( ) ( ) 2 2 2 2 2 2 2 2 2 2 a x y a x y 所围而且在圆周 x y 内部的面积。
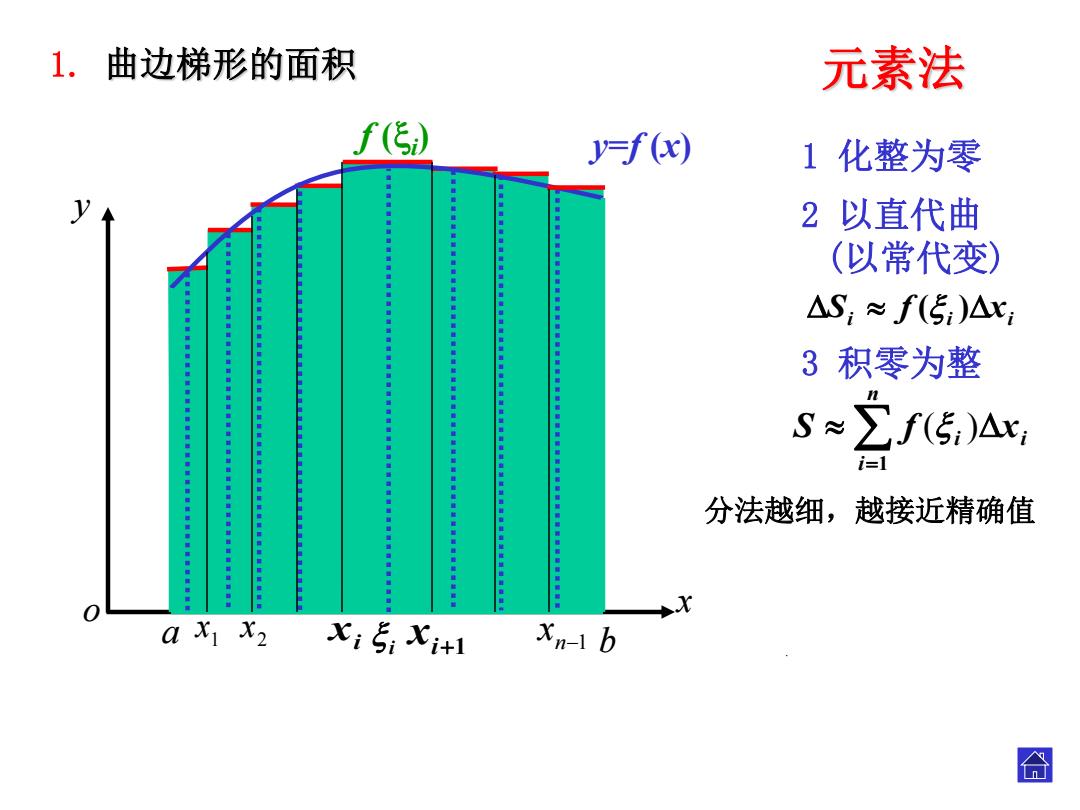
1.曲边梯形的面积 元素法 f(传) =f(x) 1化整为零 2以直代曲 (以常代变) △S:≈f(5:)△c; 3积零为整 S≈∑f(5;)△x: i=1 分法越细,越接近精确值 0 a x x2xix+ Xn-1 b 合
xi xi1 1 x i 2 x 元素法 1 化整为零 2 以直代曲 (以常代变) i i xi S f ( ) 3 积零为整 y o x y=f (x) n1 x n i i xi S f 1 ( ) a b . . 分法越细,越接近精确值 1. 曲边梯形的面积 f (i )
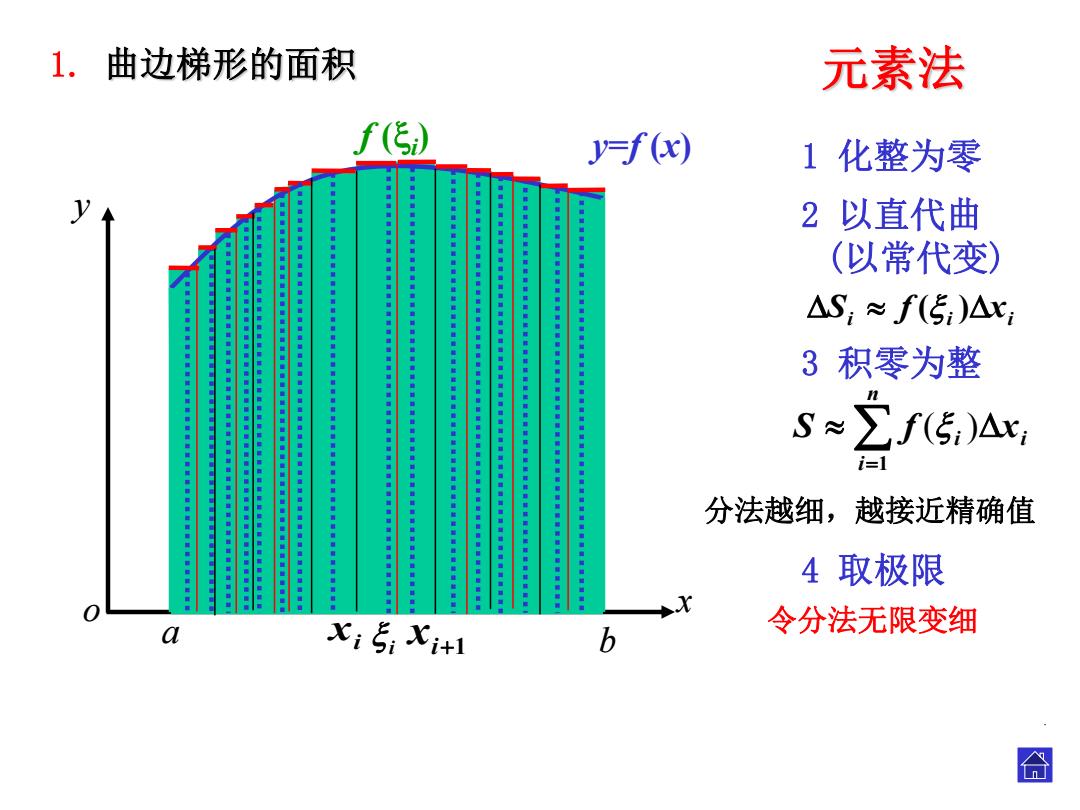
1.曲边梯形的面积 元素法 f(5) y=f(x) 1化整为零 2以直代曲 (以常代变) : △S:≈f(5:)△x: 3积零为整 S≈∑f(5)△x: i=1 : 分法越细,越接近精确值 4取极限 令分法无限变细 合
xi i xi1 元素法 4 取极限 y o x y=f (x) 令分法无限变细 . a . b . . 分法越细,越接近精确值 1 化整为零 2 以直代曲 (以常代变) 3 积零为整 n i i xi S f 1 ( ) i i xi S f ( ) 1. 曲边梯形的面积 . f (i )