
这里常量n、1、m称为量子数: 主量子数n:1,2,3,4,5,6,7. K、L、M、N、O、P、Q... 电子层 表示电子离核的平均距离,决定电子的能量 角量子数1:0,1,2,3..n-1 n表示大小,对应电 s、p、d、f. 电子亚层 子层,决定能量: 表示电子运动的空间角度分布形状 表示形状,对应电 多电子原子也与能量有关 子亚层,多电子体系 磁量子数m:0,士1,士2…士1 表示原子轨道 与n一起决定能量: 在空间上的伸展方向,与角动量的取向 m-表示方向,对应原 方 子轨道,决定轨道在 磁场中的情况 向,对应5个不同的d轨道 每一电子亚层有2+1个伸展方向(轨道) 符合这些取值的波函数都是薛定谔方程的合理解
这里常量n、l、m称为量子数: 主量子数n: 1, 2, 3, 4, 5,6,7..… K、L、M、N、O、P、Q……电子层 表示电子离核的平均距离,决定电子的能量 角量子数l:0,1,2,3…..n-1 s、p、d、f …. …. …. ….电子亚层 表示电子运动的空间角度分布形状 多电子原子l也与能量有关 磁量子数m:0,±1,±2 …..±l 表示原子轨道 在空间上的伸展方向,与角动量的取向 有关。s球形、p有px、py、pz 3个方向, d轨道有dxy、dyz、dxz、 、 5个方 向,对应5个不同的d轨道 每一电子亚层有2l+1个伸展方向(轨道) d 2 z d 2 2 x − y 符合这些取值的波函数都是薛定谔方程的合理解 n-表示大小,对应电 子层,决定能量; l-表示形状,对应电 子亚层,多电子体系 与n一起决定能量; m-表示方向,对应原 子轨道,决定轨道在 磁场中的情况
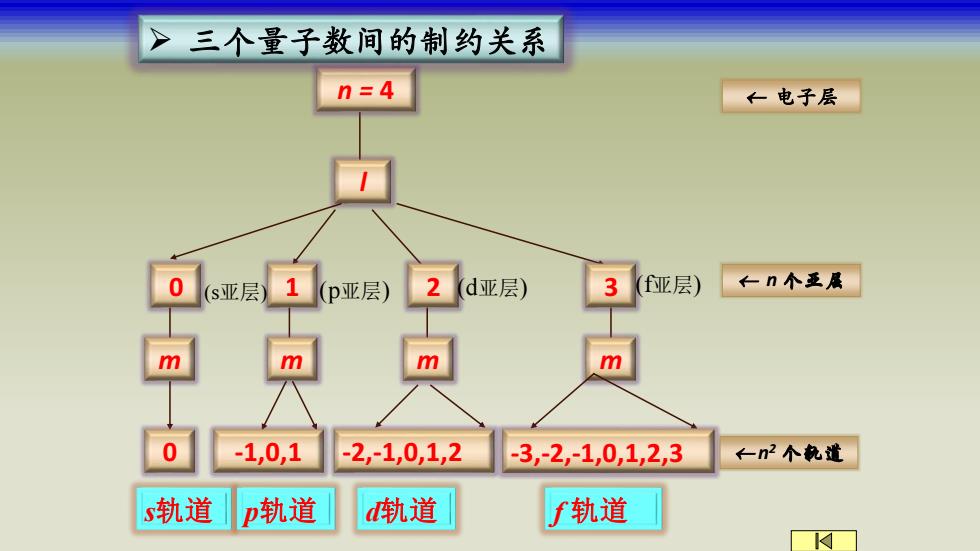
>三个量子数间的制约关系 n=4 ←电子层 0 s亚层) (p亚层) 2 d亚层) 3 亚层) ←n个亚展 m m 0 -1,0,1 -2,-1,0,1,2 -3,-2,-1,0,1,2,3 ←n2个轨道 s轨道 p轨道 d轨道 f轨道
l 0 1 2 3 m m m m n = 4 0 -1,0,1 -2,-1,0,1,2 -3,-2,-1,0,1,2,3 s轨道 p轨道 d轨道 f 轨道 (s亚层) (p亚层) (d亚层) (f亚层) ➢ 三个量子数间的制约关系 n 个亚层 n 2 个轨道 电子层

解薛定谔方程得到相应各轨道的能量为: E=-2.179x10-18Z 单位:J 式中:Z—核电核数;n一主量子数 氢原子轨道的能量高低顺序: E1s<E2s=E2p<E3s=E3p =E3d<E4s
解薛定谔方程得到相应各轨道的能量为: J n Z En 2.179 10 2 2 = − −1 8 单位: 式中:Z——核电核数;n——主量子数 氢原子轨道的能量高低顺序: E1s < E2s = E2p< E3s = E3p =E3d< E4s ……

8.2.2波高数和电子云图 电子的运动具有波动性, 在原子核周围运动时,在 空间某处出现的概率大,而在另一处出现的概率就小 试验表明:电子衍射波在空间某点的强度和电子 出现的概率密度成正比,电子波实质上就是“概率 波”,波的强度反应电子出现概率密度的大小 波动学:衍射强度∝振幅P 衍射强度∝粒子的概率密度p 粒子的概率密度p∝振幅2 波函数平正是位置与振幅的函数,所以: p y2 物理意义 表示该态电子在空间某点出现的概率密度
8.2.2 波函数和电子云图 电子的运动具有波动性, 在原子核周围运动时,在 空间某处出现的概率大,而在另一处出现的概率就小 试验表明:电子衍射波在空间某点的强度和电子 出现的概率密度成正比,电子波实质上就是“概率 波” ,波的强度反应电子出现概率密度的大小 波动学:衍射强度∝|振幅| 2 衍射强度∝粒子的概率密度p 粒子的概率密度p∝|振幅| 2 波函数Ψ正是位置与振幅的函数,所以: p ∝ |Ψ|2 |Ψ| 2表示该态电子在空间某点出现的概率密度 物理意义

解薛定谔方程得到平后,将(x,y,)坐标值代入,得到该点 的平值,振幅的平方即得电子在该点出现的概率密度 用黑点描出核外电子在空间各点的概率密度,所得图形称为 “电子云图”一电子运动的形象化图 直角坐标系(x,y,z)中解薛定谔方程式非常复杂的,为此需 要进行坐标转换一转换为球坐标(r,O,9) x=rsinθcosp y=rsin 0sin o fx y.2) z=rcos0 (r.0o) r=Vx2+y2+23 y,z)→Ψ(r,0,p) R(r).Y(e,2) 2人5条狗=x个人·y条狗≠10个人10条狗 x=2 y=5
解薛定谔方程得到Ψ后,将(x,y,z)坐标值代入,得到该点 的Ψ值,振幅的平方即得电子在该点出现的概率密度 用黑点描出核外电子在空间各点的概率密度,所得图形称为 “电子云图”——电子运动的形象化图 直角坐标系(x,y,z)中解薛定谔方程式非常复杂的,为此需 要进行坐标转换——转换为球坐标(r,θ,φ) x = rsin cos = R(r)Y(,) Ψ(x, y,z)Ψ(r,,) 2 2 2 r = x + y + z z = rcos y = rsin sin 2人·5条狗= x个人· y条狗 ≠ 10个人≠10条狗 x =? y =? =2 =5