
Bohr(玻尔)理论 两点假设 ()核外电子运动取一定的轨道。在此轨道上运动的电 子不放出能量也不吸收能量。这些轨道上的电子的角动 量必须是/2π)的整数倍,即 M=n h π (2)在一定轨道上运动的电子具有一定的能量,称为定 态。其中能量最低的称为基态,其他称为激发态。电子 从一个定态(轨道)到另一个定态(轨道)跃迁时,要 吸收或放出辐射能。这种吸收或放出的能量是一份一份 的,不连续的。 这种不连续性 一量子化,即电子的运动是量子化的
两点假设 (1) 核外电子运动取一定的轨道。在此轨道上运动的电 子不放出能量也不吸收能量。这些轨道上的电子的角动 量必须是h/(2π)的整数倍,即 2 h M = n 这种不连续性——量子化,即电子的运动是量子化的 (2) 在一定轨道上运动的电子具有一定的能量,称为定 态。其中能量最低的称为基态,其他称为激发态。电子 从一个定态(轨道)到另一个定态(轨道)跃迁时,要 吸收或放出辐射能。这种吸收或放出的能量是一份一份 的,不连续的。 Bohr(玻尔)理论
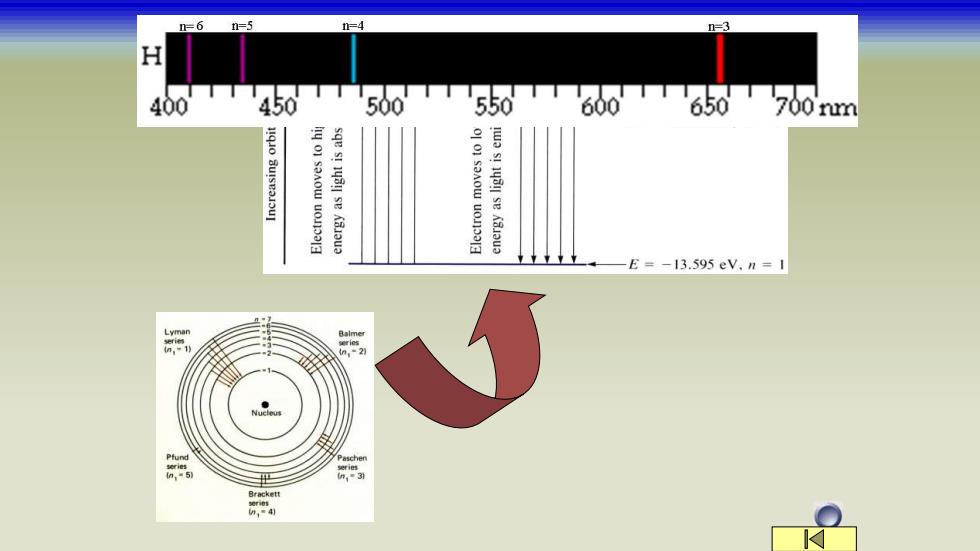
=6 n=5 =4 H 400 450 500T550T600T650700m wa sI 1y3il se Kajaua E=-13.595eV.n=1 Brackett

第一条假设:可以解释原子稳定存在的问题 第二条假设:说明核外电子运动能量只能取一些不连 续的能量状态(电子能级)。有一个能级到另一能级 跃迁时,所放出或吸收的能量是以光子的形式放出或 吸收的。所以放出或吸收的能量正好等于跃迁的两个 能级差。即: hy=E,-E,=△E E:轨道的能量 :光的频率 v=E-E h h=6.626×10-34J.s—Planck常数 轨道能量△E也是量子化的、固定的,很好地解释 了氢原子光谱的不连续性
第一条假设:可以解释原子稳定存在的问题 第二条假设:说明核外电子运动能量只能取一些不连 续的能量状态(电子能级)。有一个能级到另一能级 跃迁时,所放出或吸收的能量是以光子的形式放出或 吸收的。所以放出或吸收的能量正好等于跃迁的两个 能级差。即: h = E2 − E1 = E h E2 − E1 = E: 轨道的能量 v:光的频率 h=6.626×10-34J.s——Planck常数 轨道能量△E也是量子化的、固定的,很好地解释 了氢原子光谱的不连续性

玻尔理论的意义: (1)解释了氢原子光谱的实验事实; (2)提出了能级(轨道)的概念, 确定了Balmer公式 中n1、n2的物理意义:代表不同能量的轨道(能级),即n 代表能级的序号; (3)提出了核外电子运动时物理量的量子化特性。 玻尔理论的局限性: 建立的基础:经典物理学,采用宏观物体运动 的固定轨道概念 无法解释的试验现象:具有和 光类似的衍射现象。光是光子 的运动,具有波粒二象性
(1)解释了氢原子光谱的实验事实; (2)提出了能级(轨道)的概念,确定了Balmer公式 中n1、n2的物理意义:代表不同能量的轨道(能级),即n 代表能级的序号; (3)提出了核外电子运动时物理量的量子化特性。 无法解释的试验现象:具有和 光类似的衍射现象。光是光子 的运动,具有波粒二象性。 玻尔理论的意义: 建立的基础:经典物理学,采用宏观物体运动 的固定轨道概念 玻尔理论的局限性:

8.1.2电子的波粒二象性 二象性
8.1.2 电子的波粒二象性 二象性