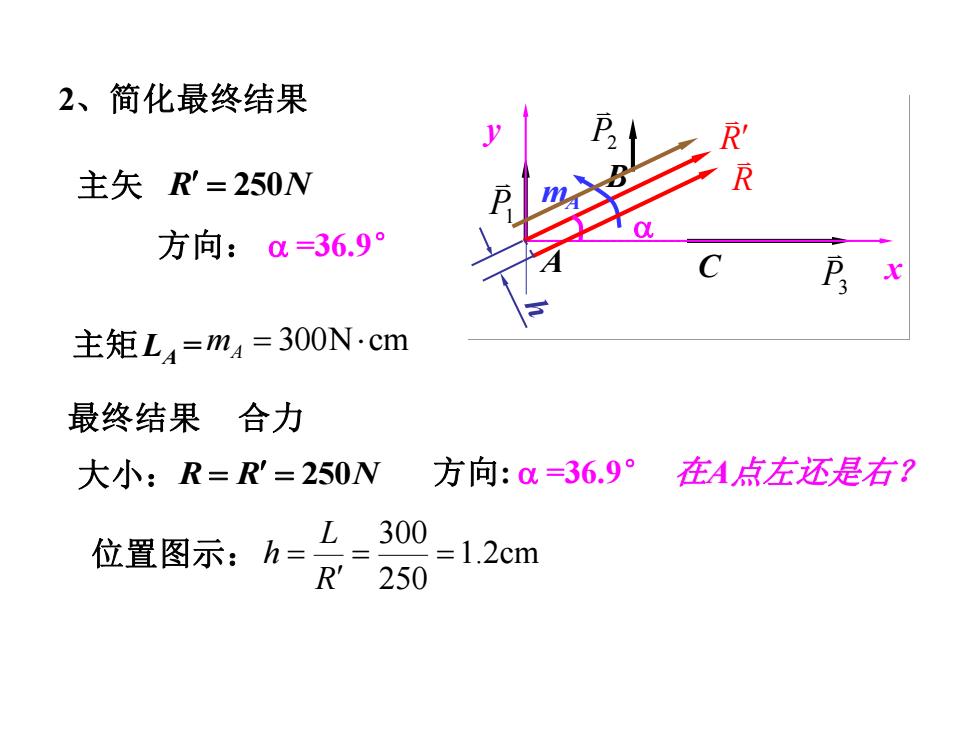
2、简化最终结果 R' 主矢R'=250N 方向:0=36.9° 主矩L4=m4=300N.cm 最终结果合力 大小:R=R'=250N 方向:0=36.9° 在4点左还是右? 位置图示:h=七=3 R'25 0=1.2cm
P1 P2 P3 A B C x y R mA = 300Ncm 2、简化最终结果 LA = 1.2cm 250 300 = = = R L h mA R 主矢 R = 250N 主矩 最终结果 合力 大小: R = R = 250N 方向: =36.9° 位置图示: 方向: =36.9° 在A点左还是右?

3.2平面任意力系的平衡条件和平衡方程 3.2.1平衡条件 平面任意力条平衡的必要与充分条件是:力条 的主矢和对任一点的主矩都等于零。即 FR=0 M=0 FR=V(∑F)2+(∑F)2 Mo=∑Mo(F)
0 0 R MO = = F 2 2 ( ) ( ) ( ) R x y O O i F F F M M = + = F 3.2 平面任意力系的平衡条件和平衡方程 3.2.1 平衡条件 平面任意力系平衡的必要与充分条件是:力系 的主矢和对任一点的主矩都等于零。即

3.2平面任意力系的平衡条件和平衡方程 3.2.2平衡方程 由于FR=V∑F)+(∑F,)2,M。=ΣMo(F) 所以 ∑F=0 ∑Fm=0 ∑Mo(F)=0 即:平面任意力条平衡的解析条件是:力系中所有各 力在其作用面内两个任选的坐标轴上投影的代数和分 别等于零,所有各力对任一点之矩的代数和等于零。 上式称为平面任意力条的平衡方程
2 2 ( ) ( ) , ( ) F F F M M R x y O O i = + = F 3.2 平面任意力系的平衡条件和平衡方程 3.2. 2 平衡方程 即:平面任意力系平衡的解析条件是:力系中所有各 力在其作用面内两个任选的坐标轴上投影的代数和分 别等于零,所有各力对任一点之矩的代数和等于零。 上式称为平面任意力系的平衡方程。 0 0 ( ) 0 xi yi O i F F M = = = F 由于 所以
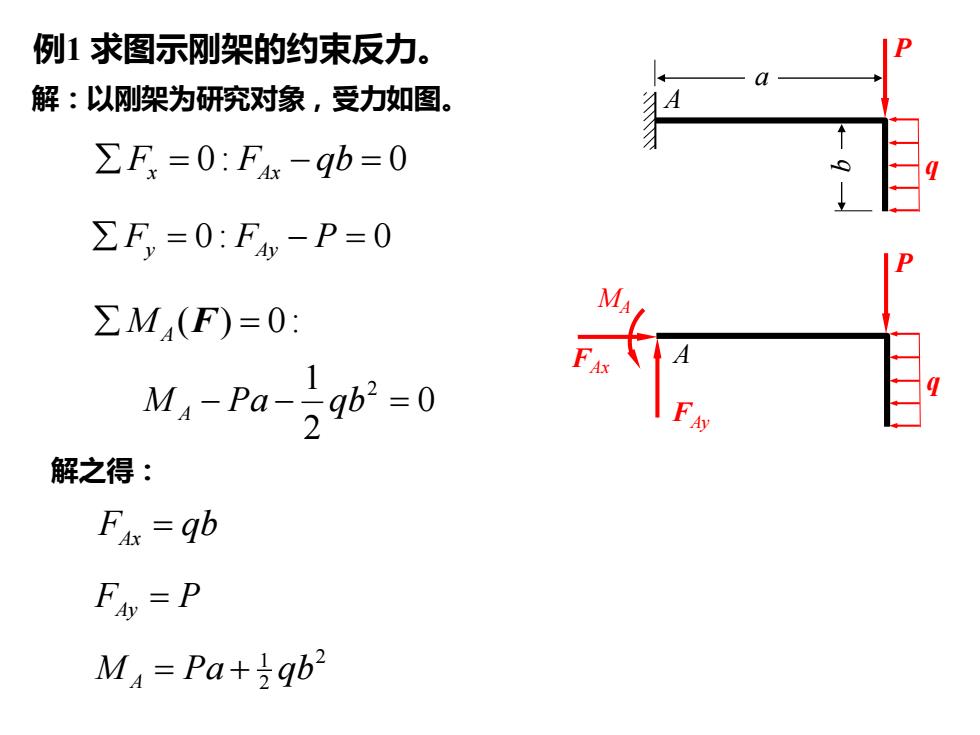
例1求图示刚架的约束反力。 解:以刚架为研究对象,受力如图。 ∑F=0:Fx-qb=0 ∑F,=0:F-P=0 ∑M4(F)=0: M-Pa-29b=0 解之得: Fs=gb Fiv=P M=Pa+igb2
解:以刚架为研究对象,受力如图。 0: 0 = − = F F qb x Ax 0 : 0 = − = F F P y Ay ( ) 0: = MA F 0 2 1 2 M A − Pa − qb = 解之得: F qb Ax = F P Ay = 2 2 1 M A = Pa + qb 例例1 求图示刚架的约束反力 1 。 A P a b q A P q FAy FAx MA
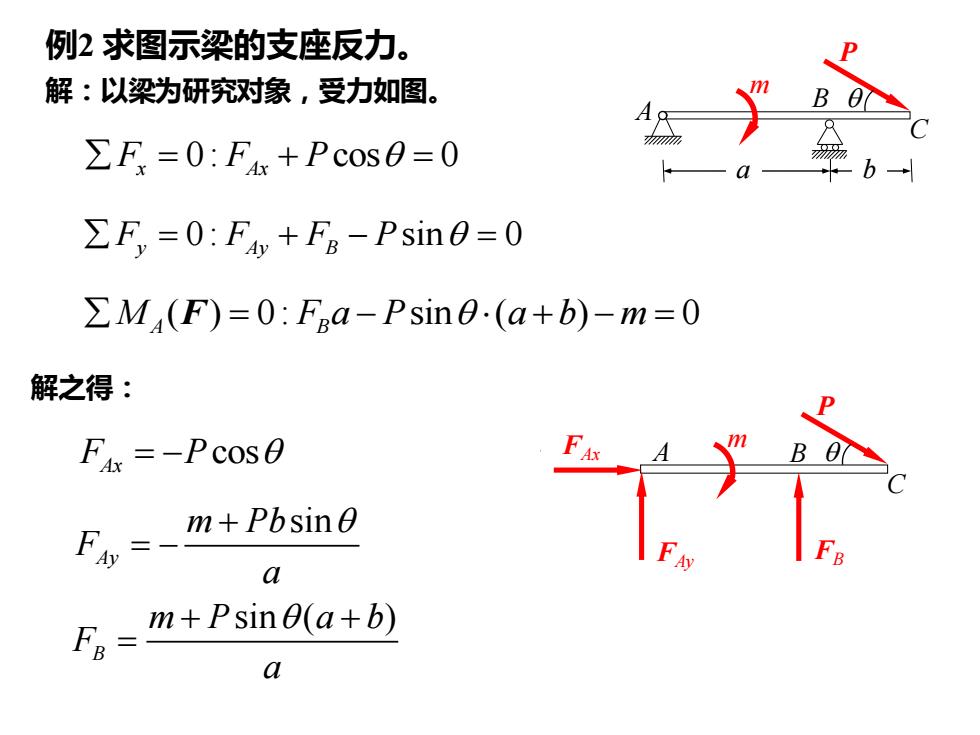
例2求图示梁的支座反力。 解:以梁为研究对象,受力如图。 ∑F=0:Fx+Pcos0=0 h ΣF,=0:Fy+FB-Psin0=0 >M(F)=0:Fga-Psine.(a+b)-m=0 解之得: Fix=-Pcos0 Ax F、 m+Pbsin a m+Psine(a+b) a
例例22求图示梁的支座反力。 解:以梁为研究对象,受力如图。 0: cos 0 = + = F F P x Ax 0 : sin 0 = + − = F F F P y Ay B ( ) 0: sin ( ) 0 = − + − = M F a P a b m A B F 解之得: cos F P Ax = − sin ( ) B m P a b F a + + = sin Ay m Pb F a + = − A B C P a b m A B C P m FAy FB FAx