3.1.4平面任意力系简化结果分析 (2)平面任意力系简化为一个合力的情形合力矩定理 如果主矩等于零,主矢不等于零,则此时平面 力系简化为一合力,作用线恰好通过简化中心。 (3) 如果主矢和主矩均不等于零,此时还可进一 步简化为一合力。如图 FR d= Mo FR
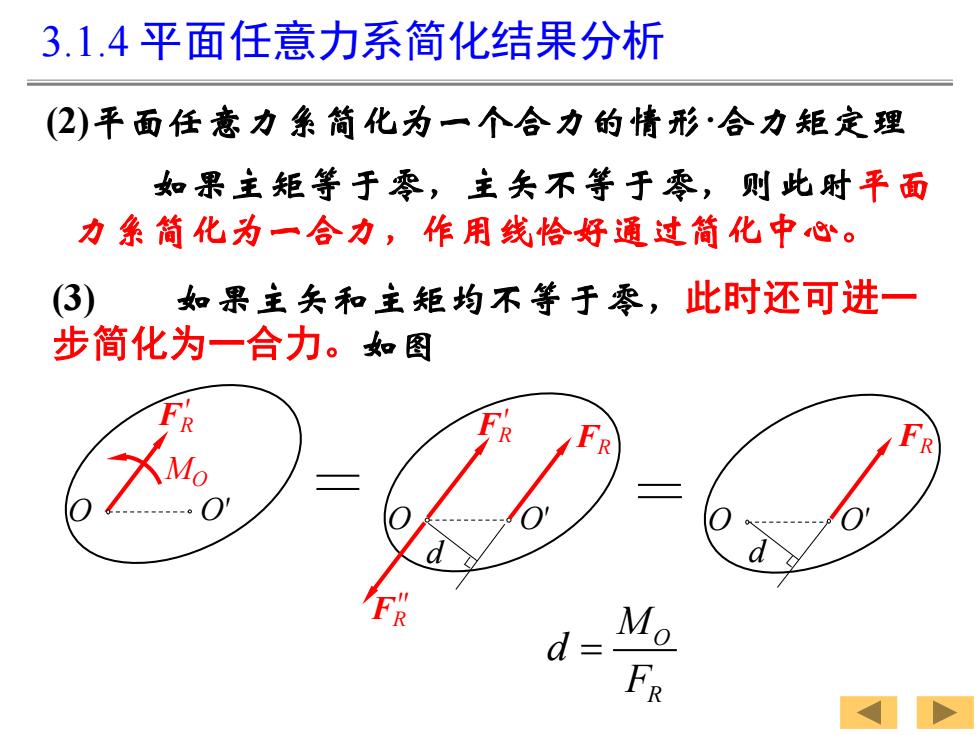
3.1.4 平面任意力系简化结果分析 (2)平面任意力系简化为一个合力的情形·合力矩定理 如果主矩等于零,主矢不等于零,则此时平面 力系简化为一合力,作用线恰好通过简化中心。 (3) 如果主矢和主矩均不等于零,此时还可进一 步简化为一合力。如图 O O′ FR ′ d FR ″ FR FR MO FR ′ O O′ d O O′ O R M d F =

3.1.4平面任意力系简化结果分析 从图中可以看出 Mo(FR)=FRd=Mo R 由主矩的定义知: M。=∑Mo(F,) 所以 Mo(FR)=∑Mo(F) 结论:平面任意力系的合力对作用面内任一点的矩等 于力系中各力对同一点的矩的代数和。这就是平面任 意力系的合力矩定理
( ) M F d M O R R O F = = ( ) M M O O i = F 结论:平面任意力系的合力对作用面内任一点的矩等 于力系中各力对同一点的矩的代数和。这就是平面任 意力系的合力矩定理。 3.1.4 平面任意力系简化结果分析 FR d O O′ 从图中可以看出 所以 由主矩的定义知: ( ) ( ) M M O R O i F F =
分布在较大范围内,不能看作集中力的荷载称分布 荷载。若分布荷载可以简化为沿物体中心线分布的平 行力,则称此力象为平行分布线苻载,简称线荷载。 思考:三角形分布载荷处理? 简化中心:A点 主矢R=89= 2 主矩 L=m,=x9k= 912 3 1 9dk 简化最终结果 R=R'= R 2 mA 1 9/2 d= 292
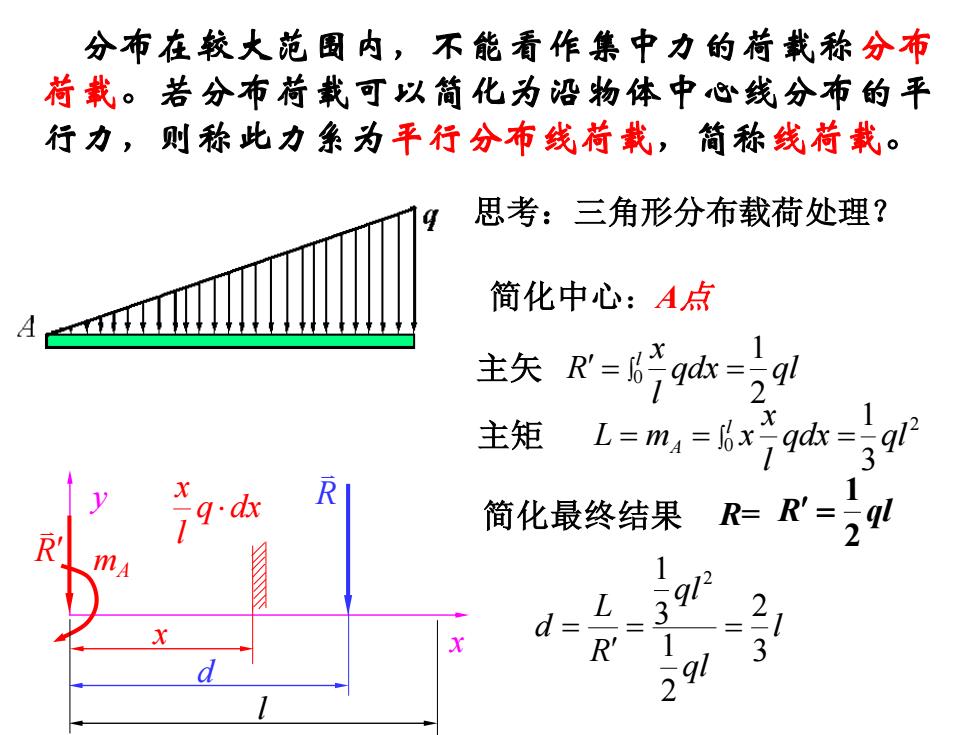
简化中心:A点 主矢 思考:三角形分布载荷处理? qdx ql l x R l 2 1 = 0 = 主矩 2 0 3 1 qdx ql l x L m x l A = = = 简化最终结果 l ql ql R L d 3 2 2 1 3 1 2 = = = y x R mA d R x l q dx l x R= R ql 2 1 = 分布在较大范围内,不能看作集中力的荷载称分布 荷载。若分布荷载可以简化为沿物体中心线分布的平 行力,则称此力系为平行分布线荷载,简称线荷载
3.1.5平行分布线荷载的简化 1、均布荷载 2、三角形荷载 O= 291 -l/2-l/2一 3、梯形荷载 可以看作一个三角形荷载和一 个均布荷载的叠加 结论: 1、合力的大小等于线荷载所组成几何 图形的面积。 2、合力的方向与线荷载的方向相同。 3、合力的作用线通过荷载图的形心
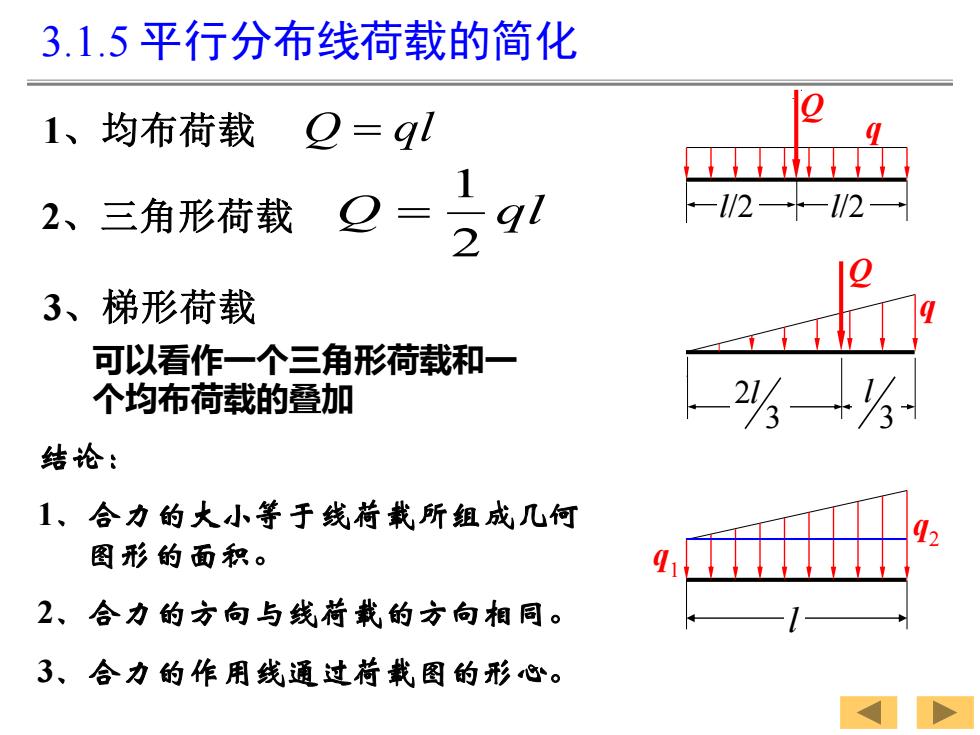
结论: 1、合力的大小等于线荷载所组成几何 图形的面积。 2、合力的方向与线荷载的方向相同。 3、合力的作用线通过荷载图的形心。 3.1.5 平行分布线荷载的简化 1、均布荷载 Q = ql 2、三角形荷载 Q ql 2 1 = 3、梯形荷载 l/2 l/2 q Q Q 2 3 l 3 l q l q2 q1 可以看作一个三角形荷载和一 个均布荷载的叠加
[例]图示力系,已知:P=100N,P2=50N,P3=200N,图中距离 单位cm。 求:1、力系主矢及对4点之矩? 2、力系简化最后结果。 P 解:1、建立坐标系 A .630 P x 2、X=∑F=P3=200N Y=∑F,=P1+P2=100+50=150N .主矢R'=VX2+Y2=V2002+1502=250N cosa-cos(R'x)-Y=200 R-250 =0.8 .0=36.9° m4=Σm4(F)=P×6=50×6=300N.cm
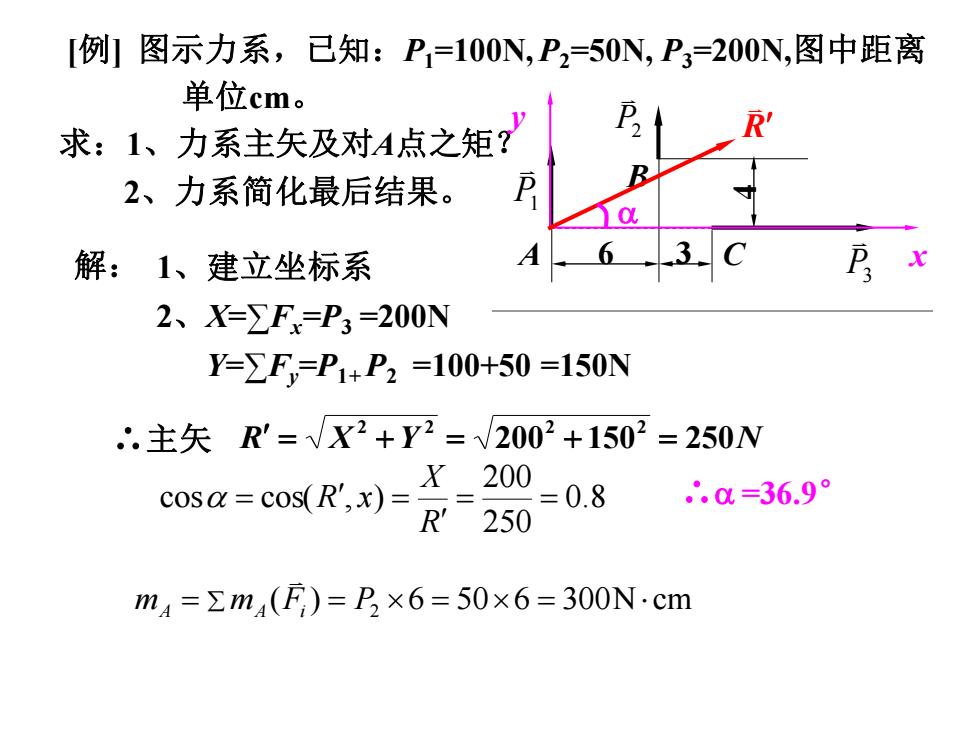
6 3 4 P1 P2 P3 A B C [例] 图示力系,已知:P1=100N, P2=50N, P3=200N,图中距离 单位cm。 求:1、力系主矢及对A点之矩? 2、力系简化最后结果。 解: 1、建立坐标系 x y 2、X=∑Fx=P3 =200N Y=∑Fy=P1+ P2 =100+50 =150N ∴主矢 R X Y 200 150 250N 2 2 2 2 = + = + = 0.8 250 200 cos cos( , ) = = = = R X R x ∴ =36.9° R mA = mA (Fi ) = P2 6 = 506 = 300Ncm