安徽科技学院：《大学物理》课程教学资源（PPT课件）第六章 狭义相对论

光速： c=3×108ms 所选光波长： 2≈5.9×10-m 干涉仪臂长约： 7=10m 地球绕太阳的公转速度： 0=3×104ms 4w= 2821w2 ≈0.4 冬 零结果！

 0.4 零结果！ 光速： 8 1 3 10 m s − c =   所选光波长： 5.9 10 m −7    地球绕太阳的公转速度： 4 1 3 10 m s − v =   干涉仪臂长约： l =10 m 2 2 2 2 c l N    v  = =

§6-2狭义相对论基本原理 与时空的相对性 6-2-1狭义相对论基本原理 狭义相对论的两条基本假设： 狭义相对论的相对性原理：在所有惯性系中，物 理定律的表达形式都相同。 ·光速不变原理：在所有惯性系中，真空中的光速 具有相同的量值c

§6-2 狭义相对论基本原理 与时空的相对性 6-2-1 狭义相对论基本原理 狭义相对论的两条基本假设： • 狭义相对论的相对性原理：在所有惯性系中，物 理定律的表达形式都相同。 • 光速不变原理：在所有惯性系中，真空中的光速 具有相同的量值c

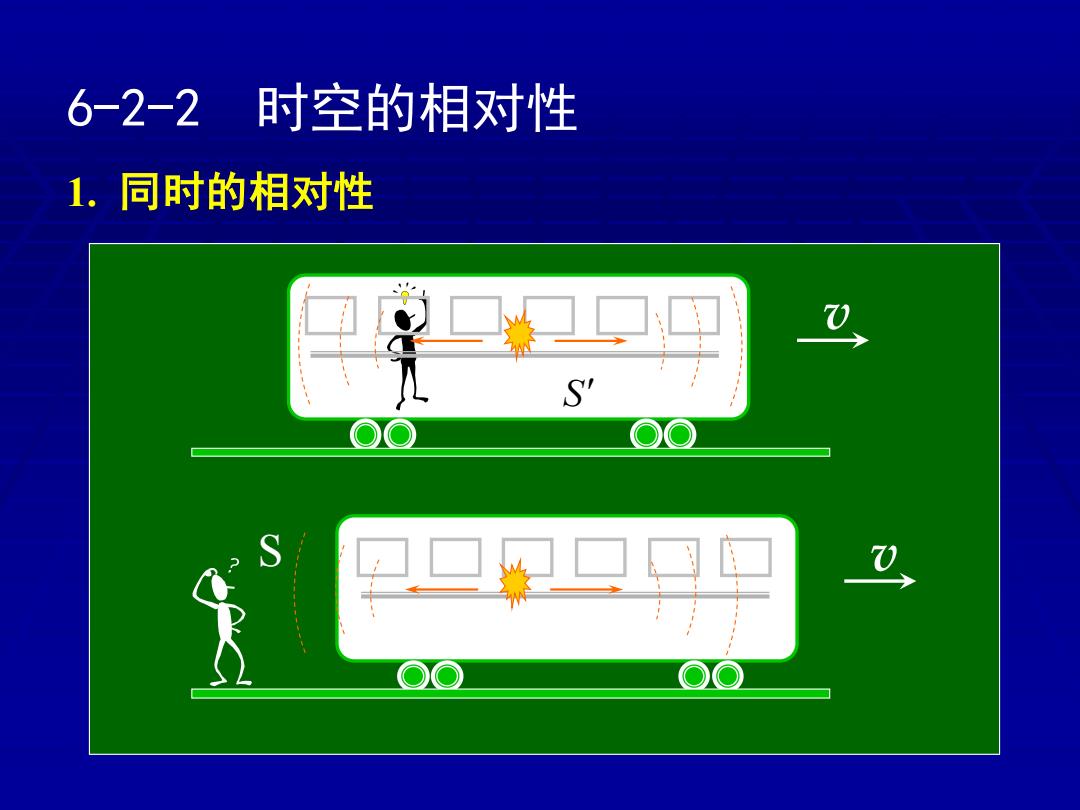
6-2-2 时空的相对性 1.同时的相对性

S v v S 6-2-2 时空的相对性 1. 同时的相对性

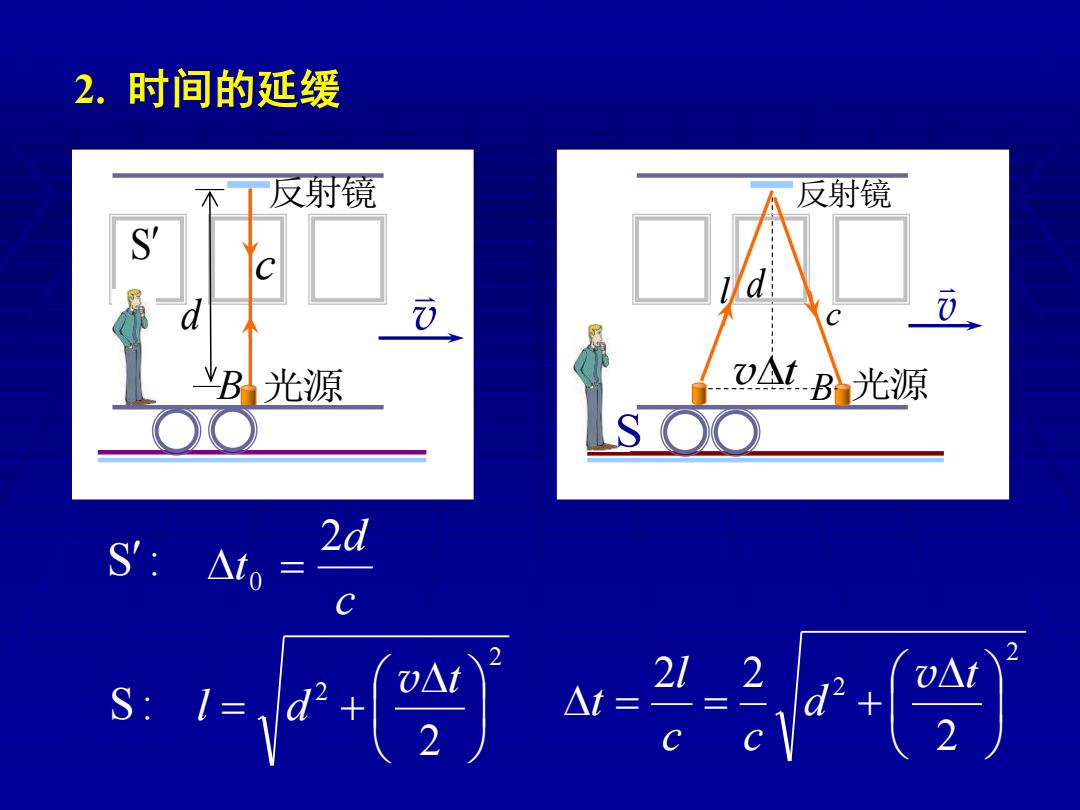
2.时间的延缓 反射镜 反射镜 B光源 VAtB光源 S':△t0= 2d s:

2. 时间的延缓 d c 反射镜 B 光源 S v  c 反射镜 B 光源 d v  l vt S c d t 2  0 = 2 2 2        = + t l d v 2 2 2 2 2         = = + t d c c l t v S: S:

从两时间式中消去d,有 21 解得： △to △t= △t>△to 71 0<<C→△t≈△to 原时：在某一参考系中同一地点先后发生两个事 件的时间间隔。 时间延缓：在S系中记录下两事件的时间间隔大于 在S系中记录到的原时

从两时间式中消去d，有 2 2 0 2 2 2 2         +        = = c t t c c l t v 解得： 2 2 0 1 c t t v −   = 0 t  t 原时：在某一参考系中同一地点先后发生两个事 件的时间间隔。 时间延缓：在S系中记录下两事件的时间间隔大于 在S’系中记录到的原时。 v  c 0  t  t