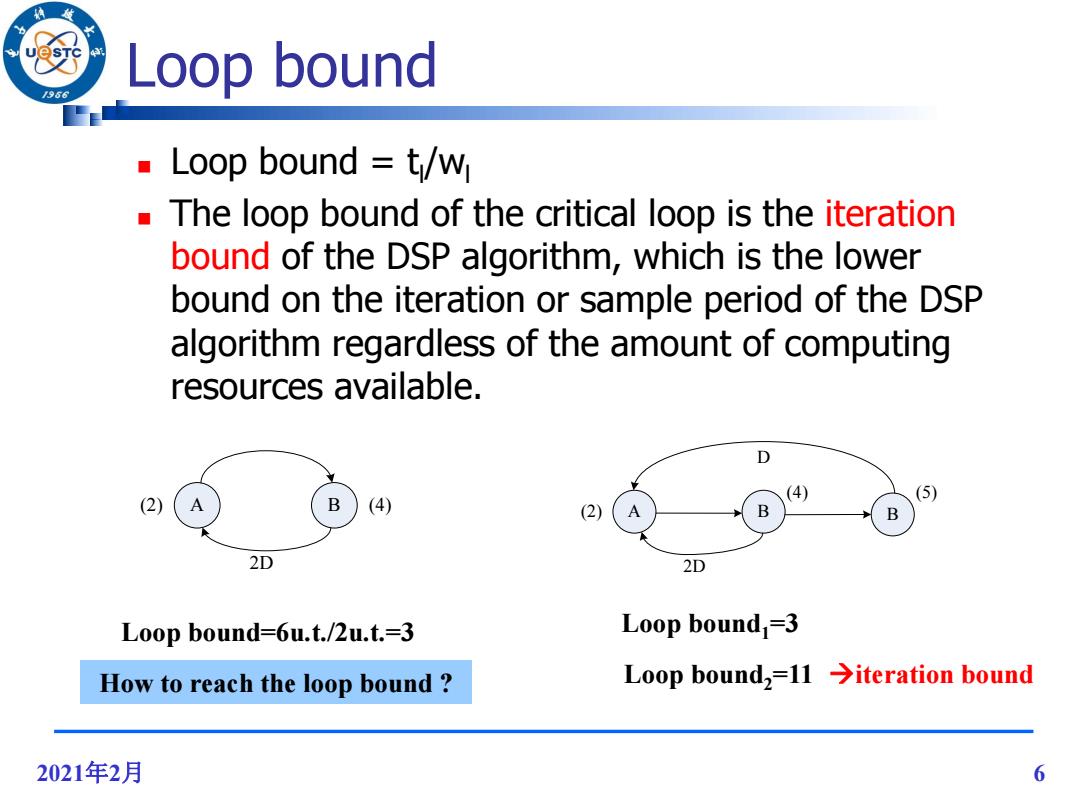
Loop bound /96 Loop bound t/w The loop bound of the critical loop is the iteration bound of the DSP algorithm,which is the lower bound on the iteration or sample period of the DSP algorithm regardless of the amount of computing resources available. D (4) (5) B (4) 2 B B 2D 2D Loop bound=6u.t./2u.t.=3 Loop bound =3 How to reach the loop bound Loop bound,=11 >iteration bound 2021年2月 6
2021年2月 6 Loop bound Loop bound = tl /wl The loop bound of the critical loop is the iteration bound of the DSP algorithm, which is the lower bound on the iteration or sample period of the DSP algorithm regardless of the amount of computing resources available. (2) A B (4) 2D B (5) D (2) A B (4) 2D Loop bound=6u.t./2u.t.=3 How to reach the loop bound ? Loop bound1=3 Loop bound2=11 iteration bound

2.3 Iteration bound 956 .n How to calculate the iteration bound? Finding all loops.>boring!!! Longest path matrix algorithm (LPM) Minimum cycle mean algorithm (MCM) Negative cycle detection algorithm 2021年2月 7
2021年2月 7 2.3 Iteration bound How to calculate the iteration bound? Finding all loops. boring!!! Longest path matrix algorithm (LPM) Minimum cycle mean algorithm (MCM) Negative cycle detection algorithm l l l L w t T max

2.4.1LPM /96 In the longest path matrix algorithm(LPM),series of matrices is constructed,the iteration bound is found by examining the diagonal elements of the matrices. L(m),m=1,2,..,d,are constructed such that value of the element I(m)is the longest computation time of all paths from delay element d to delay element d;that pass through exactly m-1 delays. If no such path exists,the I(m=-1. m Delay=m-1 (m) 72 1(m) Lm)= Longest Computation time 14 ad From i to j 2021年2月 8
2021年2月 8 2.4.1 LPM In the longest path matrix algorithm (LPM), series of matrices is constructed, the iteration bound is found by examining the diagonal elements of the matrices. L (m), m=1,2,..,d, are constructed such that value of the element l (m) i,j is the longest computation time of all paths from delay element di to delay element dj that pass through exactly m-1 delays. If no such path exists, the l(m) i,j=-1. ( ) ( ) ( ) 11 12 1 ( ) ( ) ( ) ( ) 21 22 2 ( ) ( ) ( ) 1 2 ... ... ... ... m m m d m m m m d m m m d d dd l l l l l l L l l l Delay=m-1 From i to j Longest Computation time