《电路》课程教学资源（课后课件）有例题_第16章 二端口网络

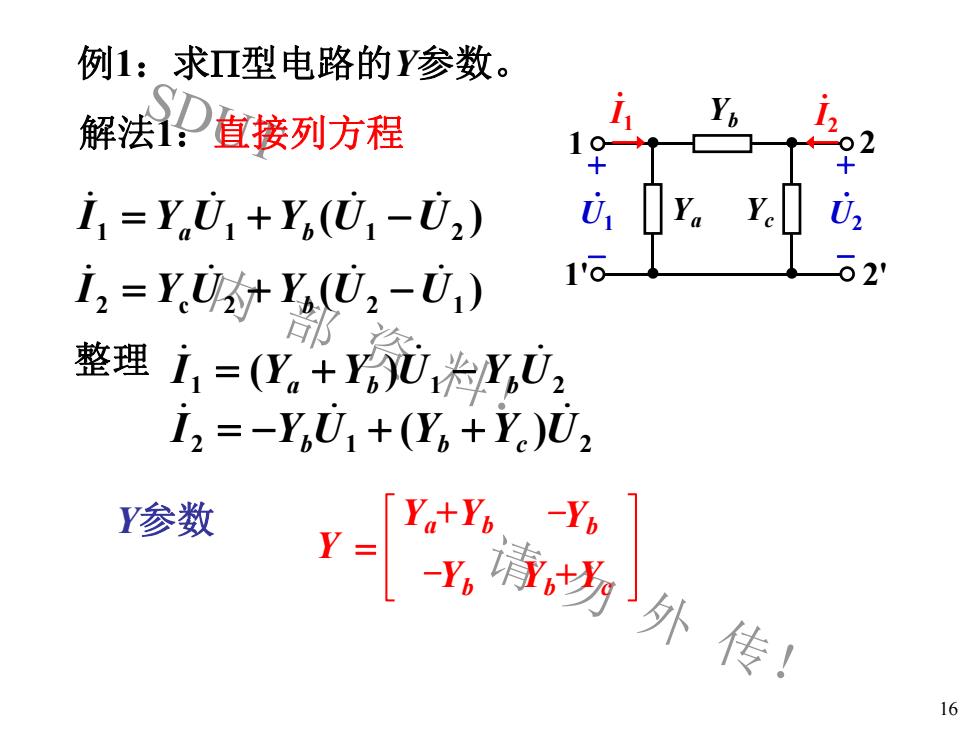
例1：求Ⅱ型电路的Y参数Ybi.2解法i？直接列方程0210++U,UYaY.i, =Y,U, +Y,(U, -U,)1002'i, = YU+ Y(U, -U)整理 i,=(Y,+UY,U,i, =-Y,U, +(Y, +Y)U,Y.+Y,-YbY参数Y =-Yh请切外传！16

SDUT 内 部 资 料！ 请 勿 外 传！ 例1：求P型电路的Y参数。 16 解法1：直接列方程 1 1' 2 2' Ya Yb Yc Y  Ya+Yb -Yb -Yb Yb+Yc .I2 + - . U1 .I1 + - . ( ) U2 1 Y U1 Y U1 U2 I a b    +  -  ( ) 2 YcU2 Y U2 U1 I b    +  -  整理 1 1 2 I   (Ya +Yb )U -YbU 2 1 2 I   -YbU + (Yb +Yc )U Y参数

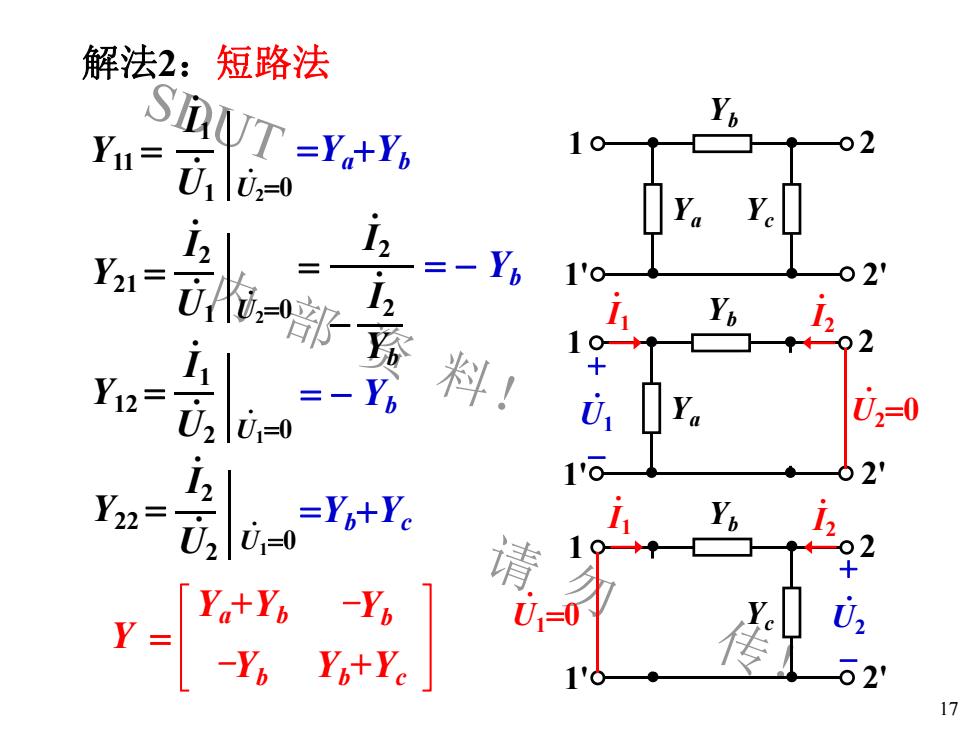
解法2：短路法SNNT -Y,+Y,Y,0210Yu= U,lu=0YaYi2i2Y1'002'Y21=T·2N-部YhiL瓷1002ii+粉Y12=YhUYU,=0UU,=0·1'002'Y22 =Y,+YciYbUU,=002请+Ya+Yb-Y,0,U,-0Y =传-Y,Y,+Yc02'1.17

SDUT 内 部 资 料！ 请 勿 外 传！ 17 解法2：短路法 Y11  .I1 . U1 . U20 Y21  .I2 . U1 . U20 Y12  .I1 . U2 . U10 Y22  .I2 . U2 . U10 Ya+Yb  - Yb  - Yb Yb+Yc 1 1' 2 2' Ya Yb Yc .I2 + - . U2 .I1 . U10 1 1' 2 2' Ya Yb Yc .I2 + - . U1 .I1 . U20 1 1' 2 2' Ya Yb Yc .I2 .I2  - Yb Y  Ya+Yb -Yb -Yb Yb+Yc

(3)互易性和对称性互易性：端口满足：Yi2=Y21有3个独立参数Yi2 = Y21 , Y11 = Y22对称性：二端口满足有2个独立参数内部资料[Yi1 Y12Y,+Yb-YbY =-YbY21 Y22.Y,+Yc对称二端口一定是互易对称二端口，而互易对称对糖后巢二克是对标三期否。分 外,传！18

SDUT 内 部 资 料！ 请 勿 外 传！ 18 (3)互易性和对称性 互易性：二端口满足：Y12  Y21 Y  Y11 Y12 Y21 Y22 Y  Ya+Yb -Yb -Yb Yb+Yc 对称性：二端口 满足 Y12  Y21 ，Y11  Y22 对称二端口一定是互易对称二端口，而互易对称 二端口不一定是对称二端口。 有3个独立参数 有2个独立参数

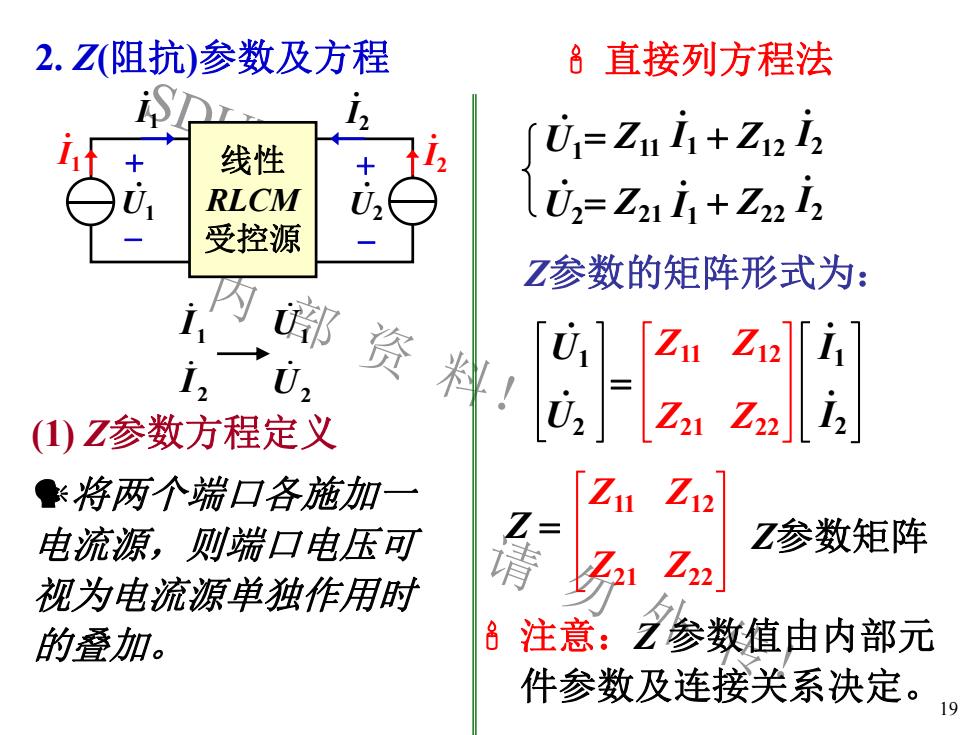
2. Z(阻抗)参数及方程8直接列方程法iSPL1U,= Zu + Z1 i,1i2I.1线性+U,= Z21i + Z22 i2URLCMU,1受控源Z参数的矩阵形式为：资u.l[Zu Zi2][ii-(1) Z参数方程定义[Z1Z12将两个端口各施加一Z=Z参数矩阵电流源，则端口电压可请Z21Z22视为电流源单独作用时吕 注意:参数值由内部元的叠加。件参数及连接关系决定。19

SDUT 内 部 资 料！ 请 勿 外 传！ 19 . U1 Z11 .I1 + Z12 .I2 . U2 Z21 .I1 + Z22 .I2 (1) Z参数方程定义 .I1 + - + - 线性 RLCM 受控源 . U1 .I2 . U2 .I1 .I2 . U1 . U2  Z11 Z12 Z21 Z22 .I1 .I2 Z11 Z12 Z21 Z22 Z  Z参数矩阵  注意：Z 参数值由内部元 件参数及连接关系决定。 2. Z(阻抗)参数及方程 Z参数的矩阵形式为： 2 1 U U   2 1 I I    直接列方程法 将两个端口各施加一 电流源，则端口电压可 视为电流源单独作用时 的叠加

(2)Z参数的的物理意义及计算和测定U1品开路法T输入阻抗；Z=iTi=0U,= Zu ii + Ziz i,U,o转移阻抗；Z21=i12=00,12=0=0一+转移阻抗;Z12=+·'线性i,li,=0RLCMC受控源输出阻抗。n2“办娇传！1I=0Z→开路阻抗参数20

SDUT 内 部 资 料！ 请 勿 外 传！ 20 Z11  . U1 .I1 .I20 输入阻抗； Z21  . U2 .I1 .I20 转移阻抗； .I1 + - + - 线性 RLCM 受控源 . U1 .I2 . U2 .I1 .I2 0 Z12  . U1 .I2 .I10 转移阻抗； Z22  . U2 .I2 .I10 输出阻抗。 0 Z  开路阻抗参数  开路法 (2) Z参数的的物理意义及计算和测定 . U1 Z11 .I1 + Z12 .I2 . U2 Z21 .I1 + Z22 .I2