
第六章相平衡(Phase equilibrium) 一、教学方案 1.掌握物质的稳定相的和二相平衡的含义。 2.掌握单组分系统相图的特点和应用。 3.掌握二组分系统气-液平衡相图的特点,包括温度-组成、压 教学目力-组成、气相组成-液相组成等相图。掌握二组分液态部分互溶系统 的 及完全不互溶系统的气-液平衡相图。 和 4.掌握二组分系统固-液平衡相图,包括生成稳定,不稳定化合 要 物及固态部分互溶相图。 5.了解三组分系统相图的含义通过相图能明确相图中各区域存 在的物质,能用杠杆规则进行计算。 6.能用相律分析相图和计算自由度数,能从实验数据绘制相图。 从相图中解决多组分系统的分离、提纯,控制产品质量等问题。 教学重 1.相律的概念及计算: 2.二组分体系的相图的应用 3.平均活度与平均活度系数。 教学难 1.二组分体系的相图 点 2.强电解质溶液理论。 教学方 1.授课全部用多媒体电子教案,告别了传统的粉笔加黑板的单 教学模式: 手 2.辅导答疑采用电子邮件及在线论坛等模式, 段 3.测验、考试的试卷由试题库自动组卷及试题分析。 教学内 容 1.§6.1相律(1学时) 及 2.§6.2单组分体系(1学时) 3.§6.3二组分体系的相图(2学时) 时 4.§6.4双液系的气一液平衡 (2学时) 分 5.§6.5三组分体系(1学时) 配 相平衡、热平衡和化学平衡是热力学在化学领域中的重要应用,也是化学热力
第六章 相平衡 (Phase equilibrium) 一、教学方案 教 学 目 的 和 要 求 1. 掌握物质的稳定相的和二相平衡的含义。 2. 掌握单组分系统相图的特点和应用。 3. 掌握二组分系统气-液平衡相图的特点,包括温度-组成、压 力-组成、气相组成-液相组成等相图。掌握二组分液态部分互溶系统 及完全不互溶系统的气-液平衡相图。 4. 掌握二组分系统固-液平衡相图,包括生成稳定,不稳定化合 物及固态部分互溶相图。 5. 了解三组分系统相图的含义通过相图能明确相图中各区域存 在的物质,能用杠杆规则进行计算。 6. 能用相律分析相图和计算自由度数,能从实验数据绘制相图。 从相图中解决多组分系统的分离、提纯,控制产品质量等问题。 教 学 重 点 1. 相律的概念及计算; 2. 二组分体系的相图的应用; 3. 平均活度与平均活度系数。 教 学 难 点 1. 二组分体系的相图 2. 强电解质溶液理论。 教 学 方 法 和 手 段 1. 授课全部用多媒体电子教案,告别了传统的粉笔加黑板的单 一教学模式; 2. 辅导答疑采用电子邮件及在线论坛等模式; 3. 测验、考试的试卷由试题库自动组卷及试题分析。 教 学 内 容 及 课 时 分 配 1. §6.1 相律 (1学时) 2. §6.2 单组分体系 (1学时) 3. §6.3 二组分体系的相图 (2学时) 4. §6.4 双液系的气— 液平衡 (2学时) 5. §6.5 三组分体系 (1学时) 相平衡、热平衡和化学平衡是热力学在化学领域中的重要应用,也是化学热力

学的主要研究对象。相平衡研究对生产和科学研究具有重大的实际意义。例如在化 学研究和化学生产过程的分离操作中,经常会遇到各种相变化过程,如蒸发、冷疑 升华、容解、结晶和萃取等,这些过程及到不同相之间的物质传递。相平衡研究是 选择分离方法、设计分离装置以及实现最佳操作的理论基础。除了分离以外,相平 衡及其基本理论还广泛应用于治金、材料科学、地质矿物学、晶体生长等学科中, 对这些部门的科研和 指导总义 本章着重讨论各种相平衡体系所遵守的一个普遍规律相律,以及各种基本 类型的相图,具体分析体系的相平衡情况与温度、压力和组成等因素的关系,并举 例说明其实际应用 S6-1相律(phase rule) 一、纯物质的稳定相与二相平衡 问题的引入:为什么高温下纯物质,气相较液、固相稳定,而在低温下,周相较气 相和液相稳定? 因为:Sm(气)>Sm(液)>Sm(固), =-S 在等压下有 aT) ,显然纯物质的化学势都是随温度的增加而增大的,其中 气态的增大率最大,固态最小。不同温度下纯物质的化学势及它们的状态如图5-11 所示意。 图6-1-1 用类似于图5一1的示意图,可得出任何转 固相相对稳定:反 势随温度与压力 的变化绘成一张三维坐标图。狂·一种物相的化学势征三维坐标图,为一曲面。这 些曲面在高温抵低压处较低,在低温高压处较高,都是一个倾斜的曲面。 二、Clapeyron方程 两相平衡时,如果两相体系的温度与压力的变化分别T和dp,两相的化学变化 分别为du(a)和du(B)。若维持两相平衡,就是过程从T T+dT +dp时又达到新的相平衡。 则μ@侧+dμa)=μ)+dμ) 两式相减,得dμ=dμ) 而dG=-SdT+d 所以-Sm(adT+Vm*(adp=-Sm*(BdT+Vm*(Bd
学的主要研究对象。相平衡研究对生产和科学研究具有重大的实际意义。例如在化 学研究和化学生产过程的分离操作中,经常会遇到各种相变化过程,如蒸发、冷凝、 升华、溶解、结晶和萃取等,这些过程及到不同相之间的物质传递。相平衡研究是 选择分离方法、设计分离装置以及实现最佳操作的理论基础。除了分离以外,相平 衡及其基本理论还广泛应用于冶金、材料科学、地质矿物学、晶体生长等学科中, 对这些部门的科研和生产有着重要的指导意义。 本章着重讨论各种相平衡体系所遵守的一个普遍规律-相律,以及各种基本 类型的相图,具体分析体系的相平衡情况与温度、压力和组成等因素的关系,并举 例说明其实际应用 §6-1 相律(phase rule) 一、纯物质的稳定相与二相平衡 问题的引入:为什么高温下纯物质,气相较液、固相稳定,而在低温下,固相较气 相和液相稳定? 因为:Sm(气) > Sm(液) > Sm(固), 在等压下有 ,显然纯物质的化学势都是随温度的增加而增大的,其中 气态的增大率最大,固态最小。不同温度下纯物质的化学势及它们的状态如图5-1-1 所示意。 图6-1-1 用类似于图5— 1的示意图,可得出任何物态的化学势都是随压力而增大。在高压下 固相相对稳定;反之在低压下气相相对稳定。如果再将物相的化学势随温度与压力 的变化绘成一张三维坐标图。狂·— 种物相的化学势征三维坐标图,为一曲面。这 些曲面在高温抵低压处较低,在低温高压处较高,都是一个倾斜的曲面。 二、Clapeyron 方程 两相平衡时,如果两相体系的温度与压力的变化分别dT和dp,两相的化学变化 分别为dµ(α)和dµ(β)。若维持两相平衡,就是过程从 T → T + dT ,p → p + dp 时又达到新的相平衡。 则 µ(α) + dµ(α) = µ(β) + dµ(β) 两式相减,得 dµ(α) = dµ(β) 而 dG = -SdT + Vdp 所以 -S m*(αdT + V m*(α)dp = -S m*(β)dT + V m*(β)dp
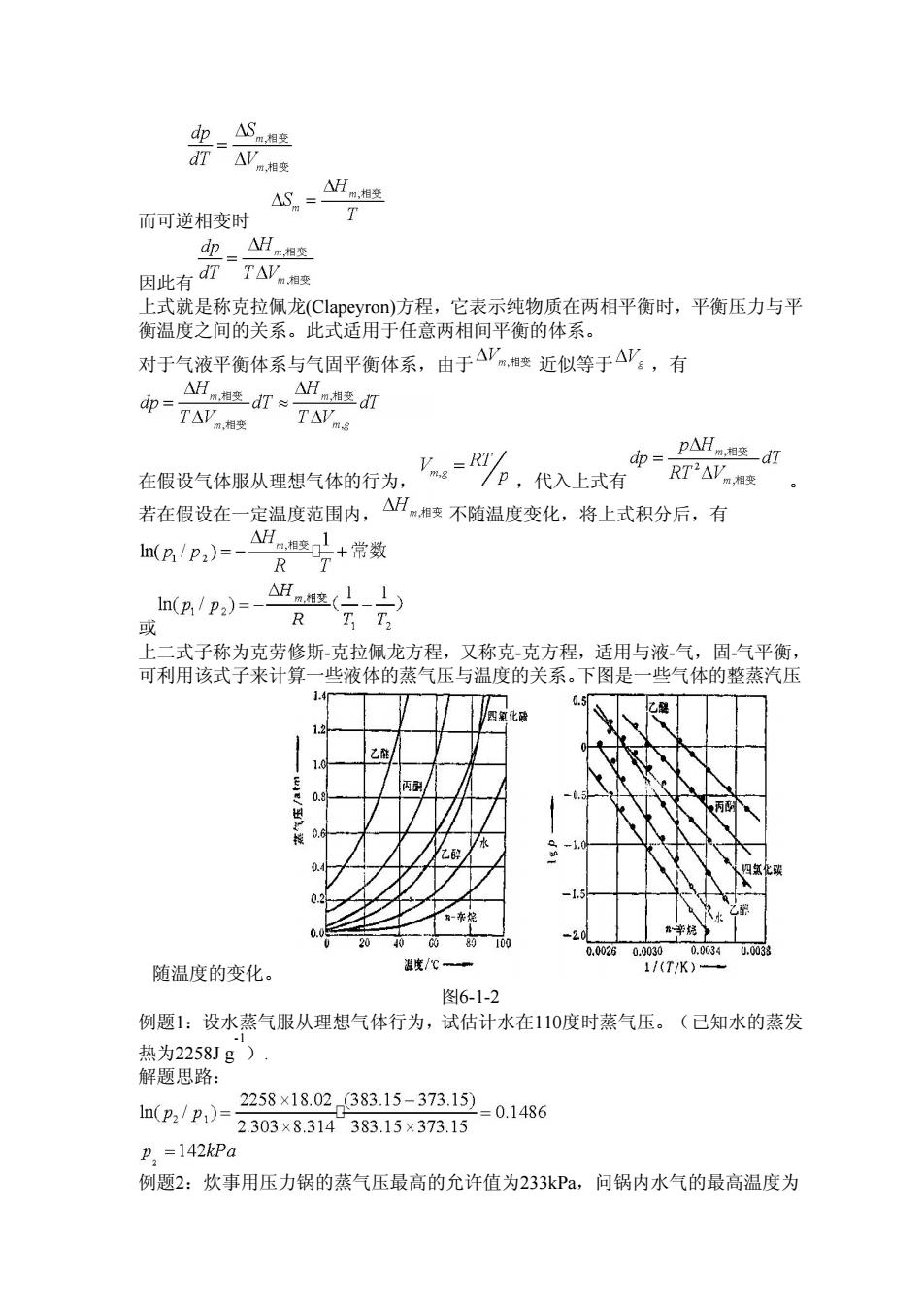
dp_△S湘空 △V变 而可逆相变时 dpH8芝 因此有TA 式就是称克拉佩龙Clapeyron))方程,它表示纯物质在两相平衡时,平衡压力与平 衡温度之间的关系。此式适用于任意两相间平衡的体系。 对于气液平衡体系与气固平衡体系,由于△严相变近似等于△,有 △H相2d打≈ dp=TAV萨 在假设气体服从理想气体的行为 y=R形,代入上式有 p△Hnad灯 若在假设在一定温度范围内, △H。变不随温度变化,将上式积分后,有 R In(p/p2)=- 或 R 式子称为克劳修斯-克拉佩龙方程,又称克克方程,适用与液气,固气平衡 可利用该式子来计算一些液体的蒸气压与温度的关系。下图是一些气体的整蒸汽压 0.5 a≤ 随温度的变化。 1TK) 图6-1-2 例题1:设水蒸气服从理想气体行为,试估计水在110度时蒸气压。(已知水的蒸发 热为2258Jg) 解题思路: 2258×18.02(383.15-373.15) h(p/p1)-2303×83143315×37315 =0.1486 p =142kPa 例题2:炊事用压力锅的蒸气压最高的允许值为233kPa,问锅内水气的最高温度为
而可逆相变时 因此有 上式就是称克拉佩龙(Clapeyron)方程,它表示纯物质在两相平衡时,平衡压力与平 衡温度之间的关系。此式适用于任意两相间平衡的体系。 对于气液平衡体系与气固平衡体系,由于 近似等于 ,有 在假设气体服从理想气体的行为, ,代入上式有 。 若在假设在一定温度范围内, 不随温度变化,将上式积分后,有 或 上二式子称为克劳修斯-克拉佩龙方程,又称克-克方程,适用与液-气,固-气平衡, 可利用该式子来计算一些液体的蒸气压与温度的关系。下图是一些气体的整蒸汽压 随温度的变化。 图6-1-2 例题1:设水蒸气服从理想气体行为,试估计水在110度时蒸气压。(已知水的蒸发 热为2258J g -1 ). 解题思路: 例题2:炊事用压力锅的蒸气压最高的允许值为233kPa,问锅内水气的最高温度为

多少? 解题思路:T=399K 三、特鲁顿(Trouton)规则 特鲁顿(Trouton)规则一些液体在正常沸点(T)下气化时, △H=8JK-0mo.可 ,可以根据这一规则,粗略估计蒸发热和正常沸点 的数值。需要注意的是,这一规则只适用于 一些不缔合的分子液体体系 四、相律(phase rule) 1、(phase) 物质从一个相转移到另一个相的过程称为相变化过程,而相平衡状态就是相变 化过程的极限,此时宏观上投有任何物质在相间传递。体系中物理性质和化学性质 全均句的 部分称为相。此处“完全均匀”,是指体系中的物质在分子水平上的均 匀混合的状态 此 即便是由多种 质构 的体 其物 性质和化学性质都边 到了完全均匀的程度,用一般的仪器已分不出其界面了,形成一个均相体系。多相 体系中,相与相之间存在明显的界面,称为相界面。越过相界面,有些性质发生突 变。例如,在373.15K的温度下,液体水和水蒸气的标准摩尔等压热容C 分别为 7548、34101·K·mo1。可见,在气一液之间相界面的两侧,水的C。具有不 同的数值 个体系所含相的数目用符号④表示气体,无论是单 气体还是混合气体,都是 个气相。对于液体,由于其互溶程度不同,可以是单相、两相或三相等。对于固 体,当化学成分不同时,就形成不同的相。但同一种固体的几种同素异晶体共存时, 如a-SiO,和B-Si0,的混合物中,虽然其化学组成都是Si0,化学性质也相同,但其 固态晶型不同,其物理性质各异,所以是两种不同的固相。均匀的固态溶液被认为 是一个相。在固态溶液中粒子的分散程度和在液态溶液中是相似的,达到了分子程 度的均匀混合,形成了“固溶体”。 2自由度(d 是义 系统原有的相数而可以独立改变的变量称为自由度,其变量数 目为自由度数,用F表示。 相平衡系统的相数与温度、压力、组成有关。例如: 单组分系统:水保持液态(单相)可在一定的温度、压力范围内任意变化:而气 液平衡(沸腾,两相)时压力一定温度(沸点)必一定,仅有一个可变:当气液固(三 相 平衡时,温度和压力均为一定值,不能变化。因此,这三种情况下的自由度数 分别称为2,1,0 双组分系统:如盐水系统,影响相态的有温度T、压力和盐的量x。当保持 高御P生服资食产度微 以改变的变量为2个 自由度2 多组分系统:直接分析F比较麻烦。必须引进规律计算
多少? 解题思路:T=399K 三、特鲁顿(Trouton)规则 特鲁顿(Trouton)规则一些液体在正常沸点(Tb)下气化时, 。可以根据这一规则,粗略估计蒸发热和正常沸点 的数值。需要注意的是,这一规则只适用于一些不缔合的分子液体体系。 四、相律(phase rule) 1、相(phase) 物质从一个相转移到另一个相的过程称为相变化过程,而相平衡状态就是相变 化过程的极限,此时宏观上投有任何物质在相间传递。体系中物理性质和化学性质 完全均匀的一部分称为相。此处“完全均匀”,是指体系中的物质在分子水平上的均 匀混合的状态,此时即便是由多种物质构成的体系,但其物理性质和化学性质都达 到了完全均匀的程度,用一般的仪器已分不出其界面了,形成一个均相体系。多相 体系中,相与相之间存在明显的界面,称为相界面。越过相界面,有些性质发生突 变。例如,在373.15K的温度下,液体水和水蒸气的标准摩尔等压热容C p,m θ分别为 75.48、34.10J·K -1 ·mol -1 。可见,在气— 液之间相界面的两侧,水的C p,m θ具有不 同的数值。 一个体系所含相的数目用符号Φ表示气体,无论是单一气体还是混合气体,都是 一个气相。对于液体,由于其互溶程度不同,可以是单相、两相或三相等。对于固 体,当化学成分不同时,就形成不同的相。但同一种固体的几种同素异晶体共存时, 如a-SiO 2和β-SiO 2的混合物中,虽然其化学组成都是SiO 2,化学性质也相同,但其 固态晶型不同,其物理性质各异,所以是两种不同的固相。均匀的固态溶液被认为 是一个相。在固态溶液中粒子的分散程度和在液态溶液中是相似的,达到了分子程 度的均匀混合,形成了“固溶体”。 2 自由度 (degrees of freedom) 定义:能够维持系统原有的相数而可以独立改变的变量称为自由度,其变量数 目为自由度数,用F表示。 相平衡系统的相数与温度、压力、组成有关。例如: 单组分系统:水保持液态(单相)可在一定的温度、压力范围内任意变化;而气 液平衡(沸腾,两相)时压力一定温度(沸点)必一定,仅有一个可变;当气液固(三 相)平衡时,温度和压力均为一定值,不能变化。因此,这三种情况下的自由度数 分别称为2,1,0 双组分系统:如盐水系统,影响相态的有温度T、压力p和盐的量x。当保持一 液相时,T、p、x 均可一定范围内改变,故自由度为3;当保持盐水溶液+盐固体两 相时,压力一定,组成(溶解度)仅是温度的关系,压力变,溶解度也变,说明可 以改变的变量为2个,自由度2。 多组分系统:直接分析F 比较麻烦。必须引进规律计算

3相律推导 对S种物质P相组成的相平衡封闭系统,对于每一个相,存在的影响因素:温 府T,压力D.组成x1,2.···,S-1注意: xB=1)共S+1变量P个相,总变 量数F=P(S+1)。对相平衡系统,限制条件如下 (1)热平衡系统压力处处相同,仅用 一个压力表示,即应扣除P)。即 p(相1)卢p(相2F· ··=p(相p) (2)热平衡系统温度处处相同,仅用一个压力表示,即应扣除(P1)个。即 T(相1=T(相2=···=T(相D (3)相平衡系统化学势守恒:对某物质B,各相的化学势相等,即 3(相1) B(相2 B(相p 存在(P1)关系式 S种物质存在S(P1)关系,也应该扣除。 (4)存在R个独立化学反应平衡式,则存在R个浓度关系等式,应扣除。 (5)存在R个其它限制条件,应扣除。 所以,达相平衡封闭系统的自由度数为 =相平衡封闭系统的总自由度数相平衡封闭系统的限制条件(或存在独立的 方程式数)=相平後 封闭系统的总自由度数(压力平衡+温度平衡+相平衡+独立反应 式+其它)的限制条件=PS+1)[(P-1)H(P-1)+SP1)十R+R] F=C-P+2其中C=SR-R 上式就是相律的表达式 应指出,上面的椎导中曾假设每一种组分都存在干每一个相中,若情识不是 样,相律的表达式不变。这是因为,如组分1不存在于(相中,则(1)相的组成变 感念T用锋来时论下速反的相平HCIGHNH三NH回 相 也化字势相等的 式也就减少了 个,所以不影响相律的形式。 (a)以等物质的量NH和HCI开始 (b)以任意量的NH,和HCI开始 分析过程:由NH,CI(sHCI(g)和NH,(g)构成的体系,体系的S=3,三种物质之 间又存在化学反应NHCI(s)=HCI(g+NH,(g)所以R=I。 平衡体系内,在同一相中若干物质的浓度(或分压)之间始终存在某种数量关 系,称其为浓度限制条件。体系中这种独立的浓度限制条件数用符号'表示。如在 上例中,若该混合物是由NHCI(s)分解而得,则体系中HCI(g)与NH(g)的浓度比保 持1:1即存在关系式y=y,气相中两物质的物质的量分数相等,所以R=1。但 应注意,物质在不同相之间保持一定的数量关系,不能算作浓度限制条件。例如 CaC0,(s)的分解,CaCO,(s)CaO(s)HC0,(g,在一定温度下,体系达成三相平衡, 虽然分解产物的物质的量相同,即nc。no2,但因CaO6)和C0,(g不是处于同一个 相中,故不能算作浓度限制条件。 4相律使用时的注意事顶 不使用于 非平衡体系。相律是各种相平衡体系 独立改变的强度性质的数目,而不能具体指出是哪些强度性质,也不能指出这些强 度性质之间的函数关系,如不能得出液体的蒸气压与温度的具体关系。相律是相图
3 相律推导 对S种物质P相组成的相平衡封闭系统,对于每一个相,存在的影响因素:温 度T,压力p,组成x1,x2,···,xS-1(注意: xB=1 ),共S+1变量P个相,总变 量数F=P(S+1)。对相平衡系统,限制条件如下 (1)热平衡系统压力处处相同,仅用一个压力表示,即应扣除(P-1)。即 p (相1)= p (相2)=···= p (相p) (2)热平衡系统温度处处相同,仅用一个压力表示,即应扣除(P-1)个。即 T (相1)= T (相2)=···= T (相p) (3)相平衡系统化学势守恒:对某物质B,各相的化学势相等,即 B(相1)= B(相2)=···= B(相p) 存在(P-1)关系式,S种物质存在S(P-1)关系,也应该扣除。 (4)存在R个独立化学反应平衡式,则存在R个浓度关系等式,应扣除。 (5)存在R'个其它限制条件,应扣除。 所以,达相平衡封闭系统的自由度数为 F=相平衡封闭系统的总自由度数-相平衡封闭系统的限制条件(或存在独立的 方程式数)=相平衡封闭系统的总自由度数-(压力平衡+温度平衡+相平衡+独立反应 式+其它)的限制条件=P(S+1)-[(P-1)+(P-1)+S(P-1)+R+R'] 即 F=C-P+2其中C=S-R-R' 上式就是相律的表达式 应指出,上面的推导中曾假设每一种组分都存在于每一个相中,若情况不是这 样,相律的表达式不变。这是因为,如组分1不存在于(1)相中,则(1)相的组成变量 就少了一个,相应地化学势相等的等式也就减少了一个,所以不影响相律的形式。 例题 试用相律来讨论下速反映的相平衡: HCl(g)+NH 3 (g) =NH 4 Cl(s) (a) 以等物质的量NH 3 和HCl开始 (b) 以任意量的NH 3和HCl开始 分析过程:由NH 4 Cl(s)、HCl(g)和NH 3 (g)构成的体系,体系的S=3,三种物质之 间又存在化学反应 NH 4 Cl(s)=HCl(g)+NH 3 (g)所以R=1。 平衡体系内,在同一相中若干物质的浓度(或分压)之间始终存在某种数量关 系,称其为浓度限制条件。体系中这种独立的浓度限制条件数用符号R’表示。如在 上例中,若该混合物是由NH 4 Cl(s)分解而得,则体系中HCl(g)与NH 3 (g)的浓度比保 持1:l即存在关系式y HCl = y NH3,气相中两物质的物质的量分数相等,所以R'=1。但 应注意,物质在不同相之间保持一定的数量关系,不能算作浓度限制条件。例如 CaC0 3 (s)的分解,CaCO 3 (s)=CaO(s)+CO 2 (g),在一定温度下,体系达成三相平衡, 虽然分解产物的物质的量相同,即n CaO =n CO2,但因CaO(s)和CO 2 (g)不是处于同一个 相中,故不能算作浓度限制条件。 4 相律使用时的注意事项 (1) 相律仅适用于相平衡系统,不使用于非平衡体系。相律是各种相平衡体系 都必须遵守的规律。但从相律得到的结论只是定性的,它只能确定平衡体系中可以 独立改变的强度性质的数目,而不能具体指出是哪些强度性质,也不能指出这些强 度性质之间的函数关系,如不能得出液体的蒸气压与温度的具体关系。相律是相图