
·测量平差通常是基于线性函数模型的当函数模型为非线性形式时,是将其用泰勒公式展开,并取其一次项化为线性形式。·对于一个实际平差问题,可建立不同形式的函数模型,相应地就有不同的平差方法。测量中常见的控制网平差方法有条件平差和间接平差两种
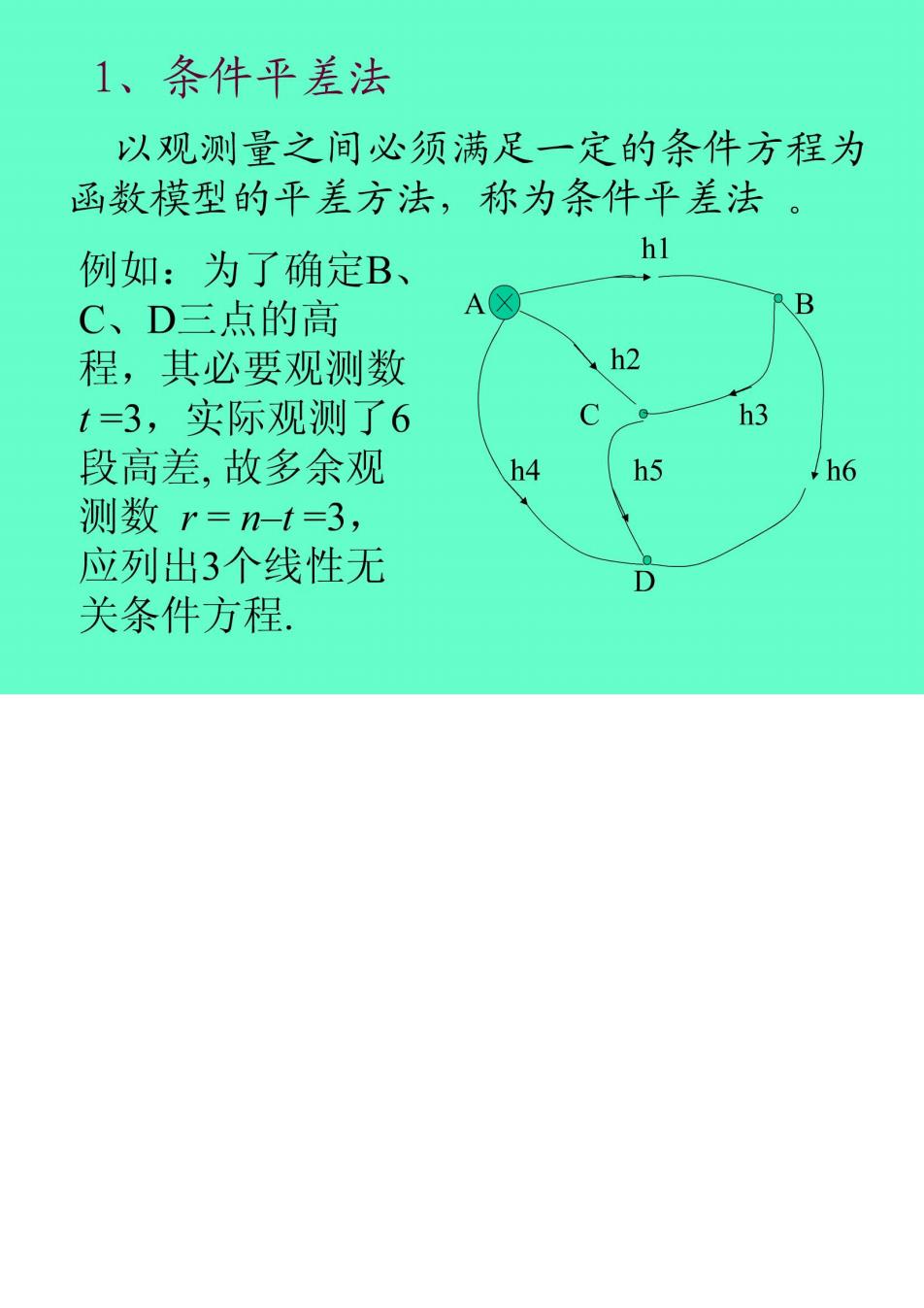
1、条件平差法以观测量之间必须满足一定的条件方程为函数模型的平差方法,称为条件平差法hl例如:为了确定B、AXBC、D三点的高h2程,其必要观测数t=3,实际观测了6h3段高差,故多余观T h6h4h5测数 r=n-t=3,应列出3个线性无D关条件方程

这个水准网可以列出7个条件方程,其中只有3个是相互独立的,我们取:h + h - h2 = 0hi + h- h = 0(a)h, +hs-h4 = Oh,表示观测量 h;的平差值。式中:这就是用平差值表达的条件方程
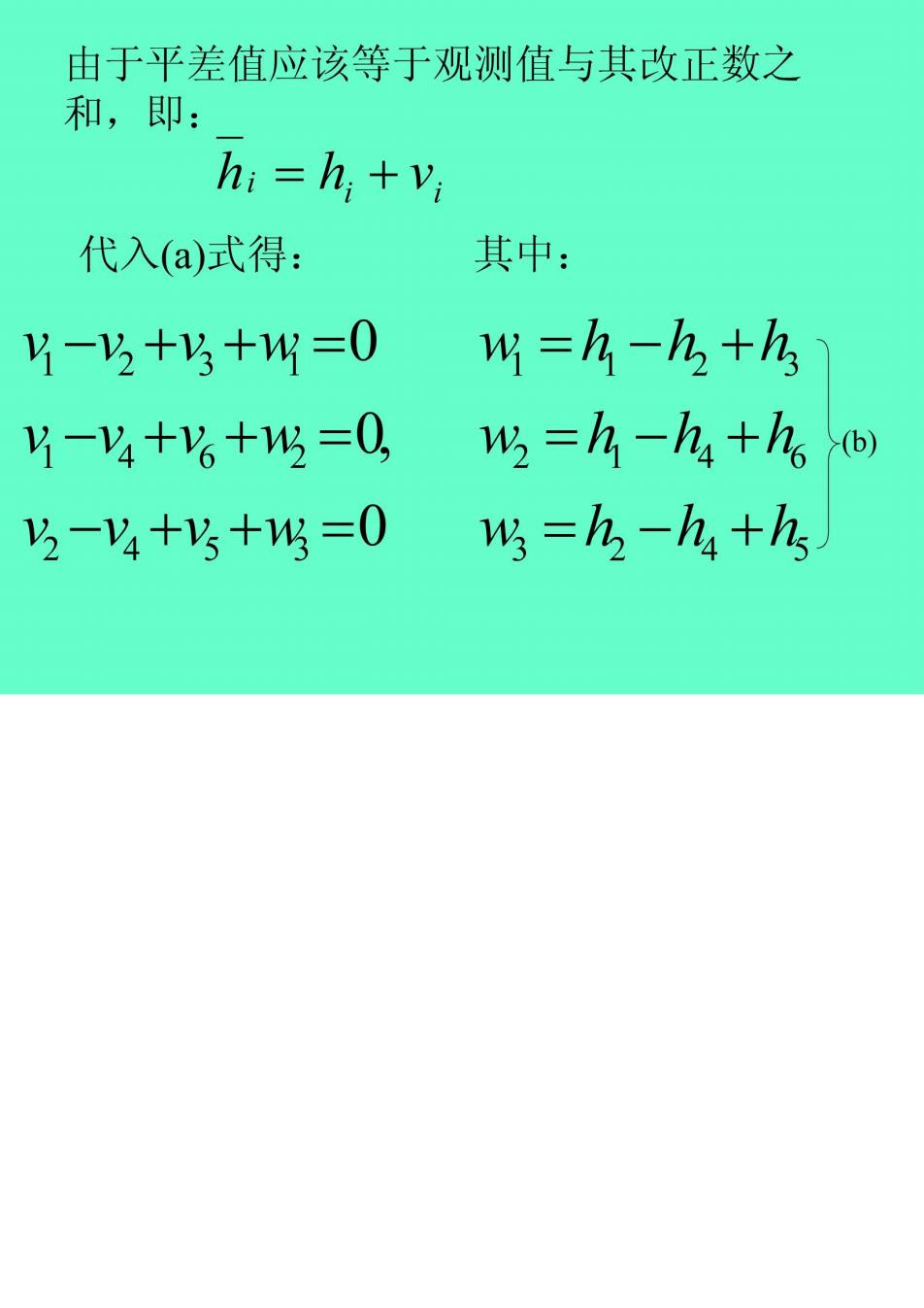
由于平差值应该等于观测值与其改正数之和,即:hi = h, +V;其中:代入(a)式得:Y-++w =0W =h -h+hY-V4+V+W =0,W =h -ha +he5(b)2-V4 +V+W =0W =h -h +hs

今OWV= (ViV2V3V4 Vsv6)T则条件方程可表达为以下矩阵形式:AV +W=0(c)这就是条件平差函数模型的一般形式