
土木工程测量学教程 第1页共8页 第八章测量误差的基本知识 本章教学目标:掌握与测量误差有关的概念,能对相关的测量问题求最或然值并进行精度评定。 本章教学重点:测量误差及计算。 本章教学难点:不等精度直接平差。 第一节测量误差概述 一、测量误差的定义 设对某量观测n次,其观测值为L1,L2,··,L,则其真误差△;定义如下: △1=L1-X(i=1,2,·,n) 二、测量误差的来源 1.仪器误差 2.观测误差 3.外界条件的影响 三、测量误差的分类 1.系统误差 在相同的观测条件下进行一系列的观测,若误差出现的数值、符号或保持不变,或按一定 的规律变化,这种误差称为系统误差。 2.偶然误差 在相同的观测条件下进行一系列观测,若单个误差出现的数值、符号都表现为偶然性,但 大量次观测的误差却具有一定的统计规律性,这类误差称为偶然误差。 需要强调指出的是,在测量过程中,有时会发生错误,亦称粗差。 四、多余观测 观测值的个数多于确定未知量所必须观测的个数。 五、测量平差的任务 概括说来,测量平差的任务有二: 1、对一系列带有偶然误差的观测值,运用概率统计的方法与最小二乘法原理来消除它们之 间的不符值,求出未知量的最或然值(亦称最可靠值或平差值)。 2、评定测量成果的精度。 六、偶然误差的特性 偶然误差列的特性如下: (1)有界性:在一定的观测条件下,误差的绝对值有一定的限值,或者说,超出一定限值 1

小工程测量学教程第2页共8页的误差,其出现的概率为零;(2)小误差的密集性:绝对值较小的误差比绝对值较大的误差出现的概率大;(3)对称性:绝对值相等的正误差与负误差出现的概率相等:(4)抵偿性:当观测次数无限增多时,偶然误差的算术平均值趋近于零,即m +A,+A A = lim 0.limn式中,“『}”为总和的符号。换言之,偶然误差的理论平均值为零。第二节衡量精度的标准一、精度的含义按不同性质的误差来定义精度。(1)精密度:表示测量结果中的偶然误差大小的程度(2)正确度:表示测量结果中的系统误差大小的程度(3)准确度:是测量结果中系统误差与偶然误差的综合,表示测量结果与真值的一致程度。现以射击为例,说明上述意义。如图8-1,c)图8-1弹孔分布示意图二、衡量精度的标准1.中误差标准差又称中误差,或称均方差、方根差。在一定的观测条件下,α的定义式为:国a=lim实际上观测个数n总是有限的,山有限个观测值的真误差△只能求得中误差的估计值(简称估值)。并采用符号(或m)表示α之估值,即有国m=6=±,本书中,常将“中误差的估值”简称为“中误差”中误差㎡的大小,反映了一列观测值的精度。不同的几列观测中,中误差越小,观测精度越高。若两列的中误差相同,则表示二者的观测精度相同。[例 8-1] 甲、乙两组对同一个平面三角形分别观测了10次,三角形内角和真误差为甲组:+4″、+3"-5"+4"-6".5+6+乙组:0"、-2"、+15"”、+1"、0″"、-2"0″、+11"、0″、+12

二不工程测量学教程第3页共8表面上看,甲组观测误差比较均匀,误差的绝对值较小,应该是甲组的观测精度高于乙组,虽然两组真误差绝对值的平均值都是4.3,但两组观测的中误差分别为J199+499 =±7.1,±4.5"mz=土可见用中误差作为衡量精度的标准,能够较好地反映观测中大误差的影响。2.极限误差根据误差理论可知,在大量等精度观测的一组误差中,误差落在区间(-,+α)(20,+2)和(-30,+3)的概率分别为:P(- <△< +g)&68.3%P(-2α <△<+2)&95.4%P(-3g <△<+3α)&99.7%规定或预期的中误差的3倍或2倍作为偶然误差的限值,即Am=30l20A=实用时,则以中误差之估值m代替。,则上式成为=3mlA=2m在测量工作中,某个误差超过限差,则相应的观测值应舍去不用,或返工重测。3. 相对误差绝对误差与其对应观测值之比称为相对误差。相对误差是个无名数,通常化为分子为1的形式,即1/T(T为相对误差的分母)。第三节误差传播定律如何根据观测值的中误差推求观测值函数的中误差,就是本节要讨论的问题。在测量上用以阐述独立观测值中误差和函数中误差之间关系的定律,称之为误差传播定律。误差传播定律的主要公式:1.按性质先列出函数关系式z= f(xj,x2,A,x,)2.对函数式进行全微分,得出函数真误差与观测值之间的关系式=[%) +(%)++ +(%)4R3.然后代入误差传播定律公式,计算函数的中误差 (%) (%) + +(%)mLax
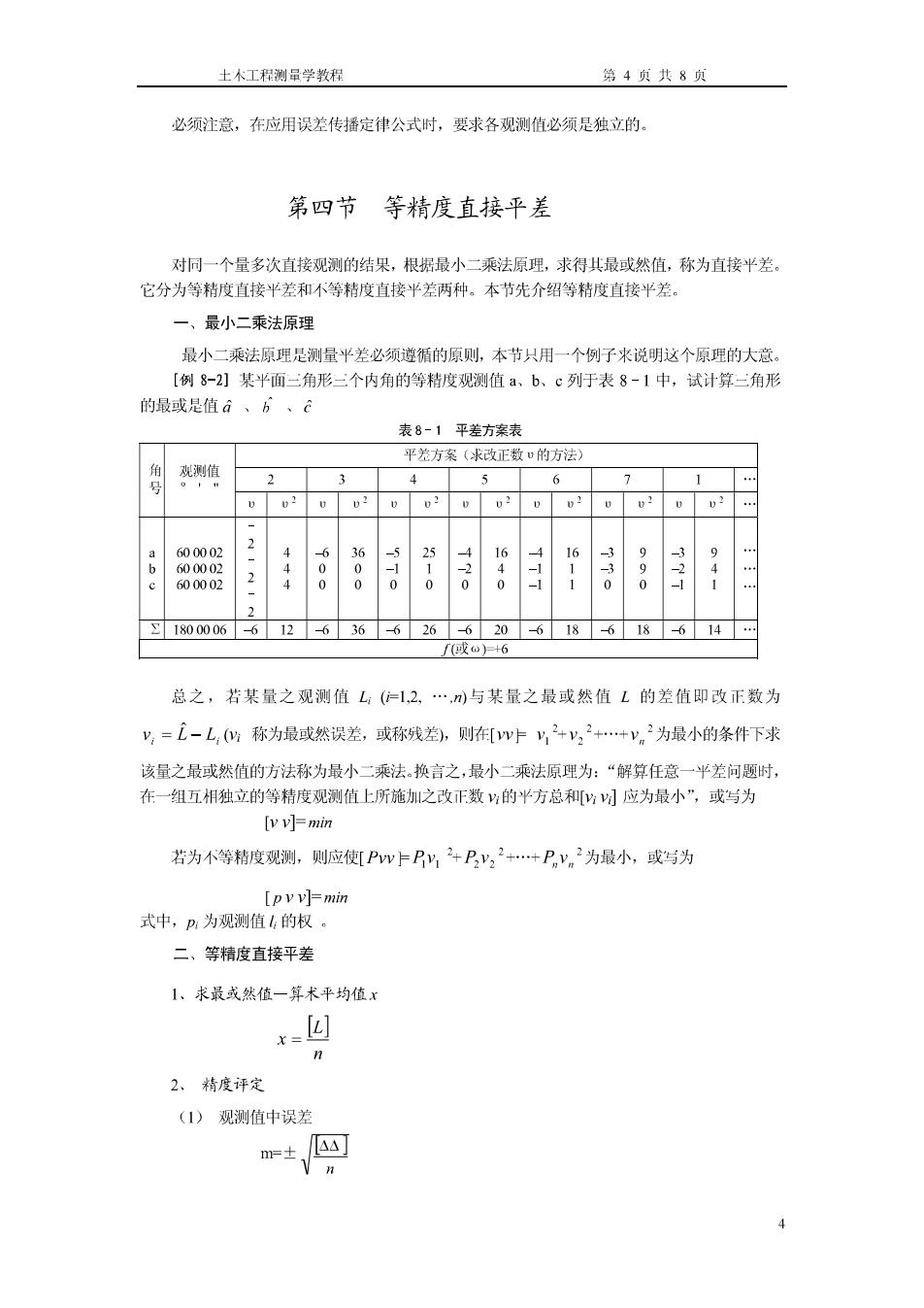
木工程测量学教程第4页共8页必须注意,在应用误差传播定律公式时,要求各观测值必须是独立的。第四节等精度直接平差对同一个量多次直接观测的结果,根据最小二乘法原理,求得其最或然值,称为直接平差。它分为等精度直接平差和不等精度直接平差两种。本节先介绍等精度直接平差。一、最小二乘法原理最小二乘法原理是测量平差必须遵循的原则,本节只用一个例子来说明这个原理的大意。[例8-2】某平面三角形三个内角的等精度观测值a、b、列于表8-1中,试计算二角形的最或是值α6、表8-1平差方案表平差方案(求改正数"的方法)角观测值121022211500总之,若某量之观测值L(=1,2,,n)与某量之最或然值L的差值即改正数为V=-L,称为最或然误差,或称残差),则在[*+,…+v为最小的条件下求该量之最或然值的方法称为最小二乘法。换言之,最小二乘法原理为:“解算任意一平差问题时,在一组五相独立的等精度观测值上所施加之改正数的半方总和[应为最小”,或写为[vv]-min若为不等精度观测,则应使[PwPy2+Pv2++P,v2为最小,或写为[pvv]=min式中,p为观测值!.的权。二、等精度直接平差1、求最或然值一算术平均值x2、精度评定(1)观测值中误差±国

二不工程测量学教程第5页共8页而4,=L-X(i-l, 2, , n)山于未知量的真值往往是无法知道的,因此其误差△也无法求得,所以一般不能直接用上式来求观测值中的误差。但是未知量的最或然值x与观测值L,的差数(改正数)是可以求得的,即,=x-L,(i-l, 2, , n)为了评定精度,需要导出山改正数a来计算观测值中误差的公式。间上式又称为白塞尔公式,用以在等精度观测时用改正数计算观测值的中误差。(2)算术平均值中误差[]_-+L(a)m=±Jn上式表明,算术平均值的中误差较单一观测值的中误差缩小了Vn倍,也就是算术平均值的精度提高了倍。设m=l,山(a)可得m与n之间的关系如表8-2所示。表8-2m与n之关系比较51020n aaaa a 山表8-4可知,当n增大时,m即随之减小,也就是说,增加观测次数可以提高算术平均值的精度。但n增至6次以上时,m之减小已极有限,故不能单从增大n来提高精度。提高精度最经济而可靠的办法是:采用精度较高的仪器、改进观测方法、提高操作技能、选择最有利的外界环境等。【例8-3】对某段距离等精度丈量了九个测回,观测结果列于表8-3中。试计算该段距离的算术平均值、观测值中误差、算术平均值中误差和相对中误差。[解]全部计算在表8-3中进行。表8-3等精度观测精度计算计算Lm著经药51_125.75 m+$3国±2.7 cnm02411-m=±0.9cmm125.7K--13972139001317