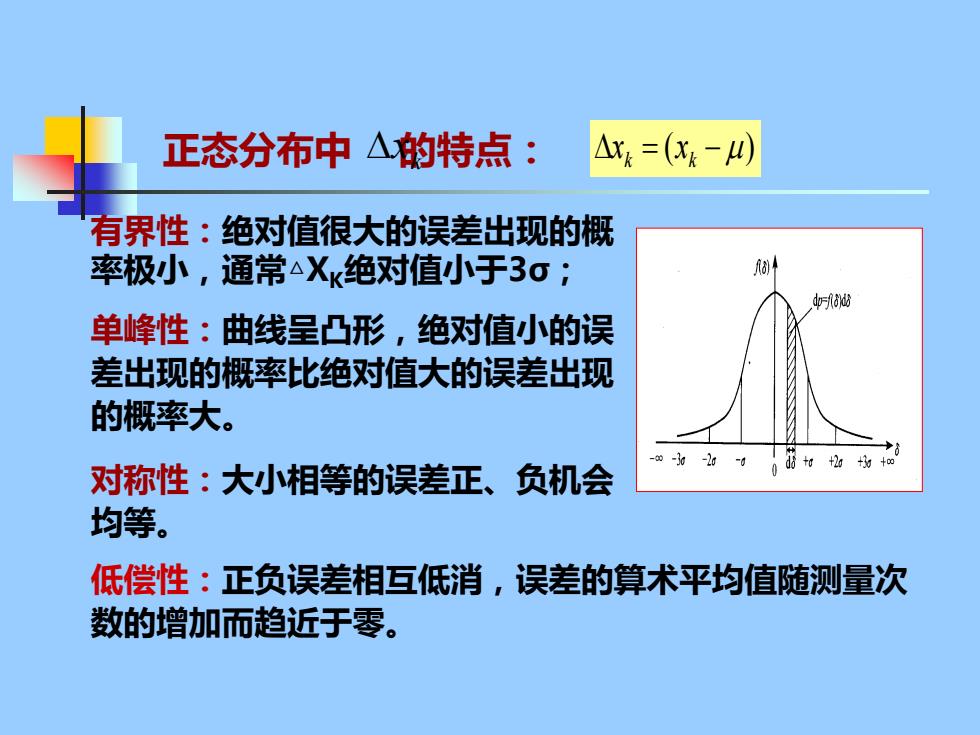
正态分布中△的特点: △x=(X-四) 有界性:绝对值很大的误差出现的概 率极小,通常△Xk绝对值小于3o: da 单峰性:曲线呈凸形,绝对值小的误 差出现的概率比绝对值大的误差出现 的概率大。 0-30-2g -0 对称性:大小相等的误差正、负机会 均等。 低偿性:正负误差相互低消,误差的算术平均值随测量次 数的增加而趋近于零
有界性:绝对值很大的误差出现的概 率极小,通常△XK绝对值小于3σ; 单峰性:曲线呈凸形,绝对值小的误 差出现的概率比绝对值大的误差出现 的概率大。 对称性:大小相等的误差正、负机会 均等。 = ( − ) k k x x 低偿性:正负误差相互低消,误差的算术平均值随测量次 数的增加而趋近于零。 正态分布中 的特点: k x
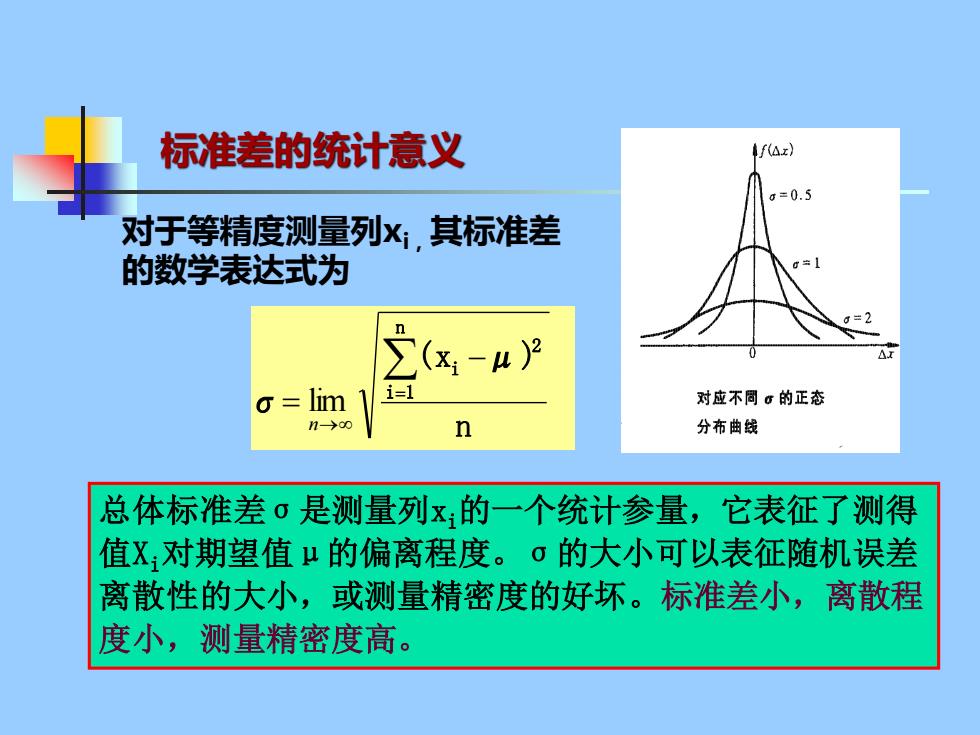
标准差的统计意义 f(Az) =0.5 对于等精度测量列x;,其标准差 的数学表达式为 (X-4)2 o=lim 对应不周。的正态 n>0 n 分布曲线 总体标准差·是测量列x:的一个统计参量,它表征了测得 值X对期望值μ的偏离程度。·的大小可以表征随机误差 离散性的大小,或测量精密度的好坏。标准差小,离散程 度小,测量精密度高
总体标准差σ是测量列xi的一个统计参量,它表征了测得 值Xi对期望值μ的偏离程度。σ的大小可以表征随机误差 离散性的大小,或测量精密度的好坏。标准差小,离散程 度小,测量精密度高。 标准差的统计意义 n ( x μ ) σ n i 1 2 i = → − = n lim 对于等精度测量列xi,其标准差 的数学表达式为
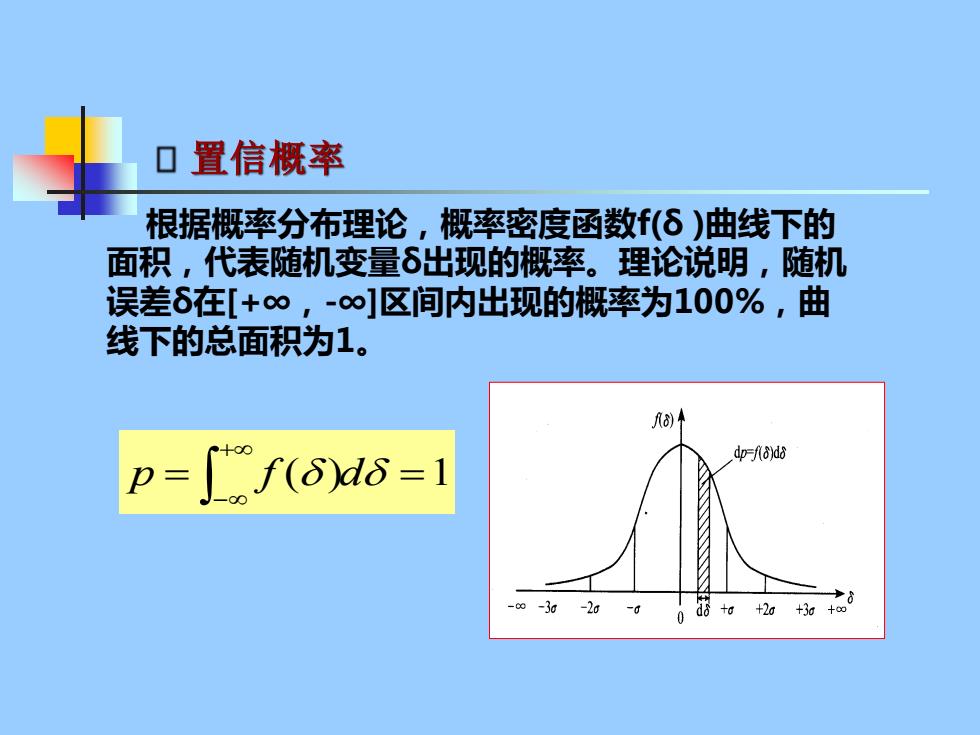
0置信概率 根据概率分布理论,概率密度函数(6)曲线下的 面积,代表随机变量6出现的概率。理论说明,随机 误差δ在[+∞,-∞]区间内出现的概率为100%,曲 线下的总面积为1。 Ao) p=rf(δd6=1 dpn)ds -0-30-2 -0 0 +o +20+30+∞
= ( ) =1 + − p f d 置信概率 根据概率分布理论,概率密度函数f(δ )曲线下的 面积,代表随机变量δ出现的概率。理论说明,随机 误差δ在[+∞,-∞]区间内出现的概率为100%,曲 线下的总面积为1
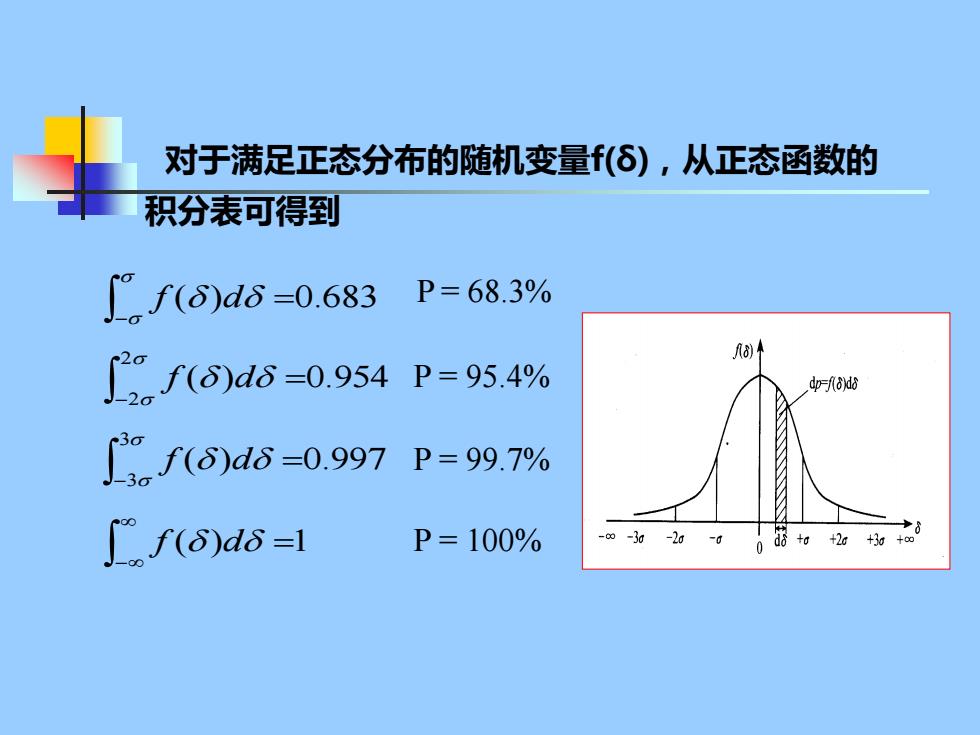
对于满足正态分布的随机变量(6),从正态函数的 积分表可得到 .f(δ)d6=0.683 P=68.3% )个 f8)d6=0.954P=95.4% dp-f8Xd8 .f()d6=0.997 P=99.7% Cf(δ)d6=1 P=100% -∞-30-2-0 0筋2+中
对于满足正态分布的随机变量f(δ),从正态函数的 积分表可得到 ( ) 0.683 − = f d ( ) 0.954 2 −2 = f d ( ) 0.997 3 −3 = f d ( ) 1 − f d = P = 68.3% P = 95.4% P = 99.7% P = 100%

©置信区间 在误差分布的范围内,取一个确定的区间[+a, ],则误差出现在此区间的概率 +a Jf(o)d。 -a P称为置信概率;相应的区间+a,a]称 为置信区间:a为置信区间的半宽
在误差分布的范围内,取一个确定的区间[+a,- a],则误差出现在此区间的概率 + − = a a p f d ( ) P 称为置信概率;相应的区间[+a,-a]称 为置信区间;a为置信区间的半宽。 ◎置信区间