
(2)随机误差 在相同条件下,对同一测量量的多次测量过程中 每次测量的误差大小正负难以预测,其特征是它的不 确定性。 随机误差的来源:测量过程中各种随机的或不确定 的因素,例如温度、湿度、电压的起伏,测量环境中 电场、磁场的随机扰动,被测量本身的微小变化等。 如果测量次数很多时,随机误差的出现符合一定的统计 规律。可采取多次测量取平均的方法减少其影响
(2)随机误差 ◼在相同条件下,对同一测量量的多次测量过程中, 每次测量的误差大小正负难以预测,其特征是它的不 确定性。 ◼随机误差的来源:测量过程中各种随机的或不确定 的因素,例如温度、湿度、电压的起伏,测量环境中 电场、磁场的随机扰动,被测量本身的微小变化等。 如果测量次数很多时,随机误差的出现符合一定的统计 规律。可采取多次测量取平均的方法减少其影响

(3)粗大误差 由于实验差错造成的粗差。例如:读数错误、记录错 误、计算错误等。这属于不正常的测量范畴,应尽量 避免。明显超出规定条件下预期的误差称为粗大误差。 一般将含有粗差的测量值称为坏值或者异常值。在实 验测量过程中或数据处理时要尽量剔除这些坏值。 坏值的剔出原则:对于满足正态分布的随机变量,一般 取士3o为误差极限,误差大于±3o的测量值视为坏值
(3)粗大误差 ◼由于实验差错造成的粗差。例如:读数错误、记录错 误、计算错误等。这属于不正常的测量范畴,应尽量 避免。明显超出规定条件下预期的误差称为粗大误差。 ◼一般将含有粗差的测量值称为坏值或者异常值。在实 验测量过程中或数据处理时要尽量剔除这些坏值。 坏值的剔出原则:对于满足正态分布的随机变量,一般 取±3σ为误差极限,误差大于±3σ的测量值视为坏值
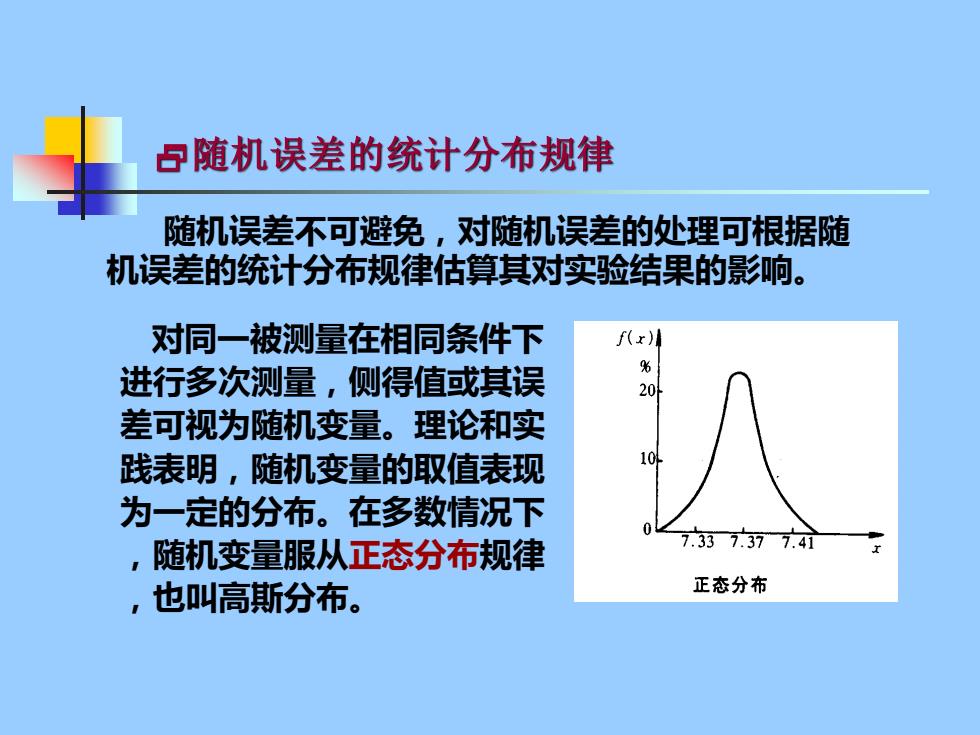
日随机误差的统计分布规律 随机误差不可避免,对随机误差的处理可根据随 机误差的统计分布规律估算其对实验结果的影响。 对同一被测量在相同条件下 fx川 进行多次测量,侧得值或其误 20 差可视为随机变量。理论和实 践表明,随机变量的取值表现 为一定的分布。在多数情况下 ,随机变量服从正态分布规律 .337.377.41i ,也叫高斯分布。 正态分布
对同一被测量在相同条件下 进行多次测量,侧得值或其误 差可视为随机变量。理论和实 践表明,随机变量的取值表现 为一定的分布。在多数情况下 ,随机变量服从正态分布规律 ,也叫高斯分布。 随机误差不可避免,对随机误差的处理可根据随 机误差的统计分布规律估算其对实验结果的影响。 随机误差的统计分布规律
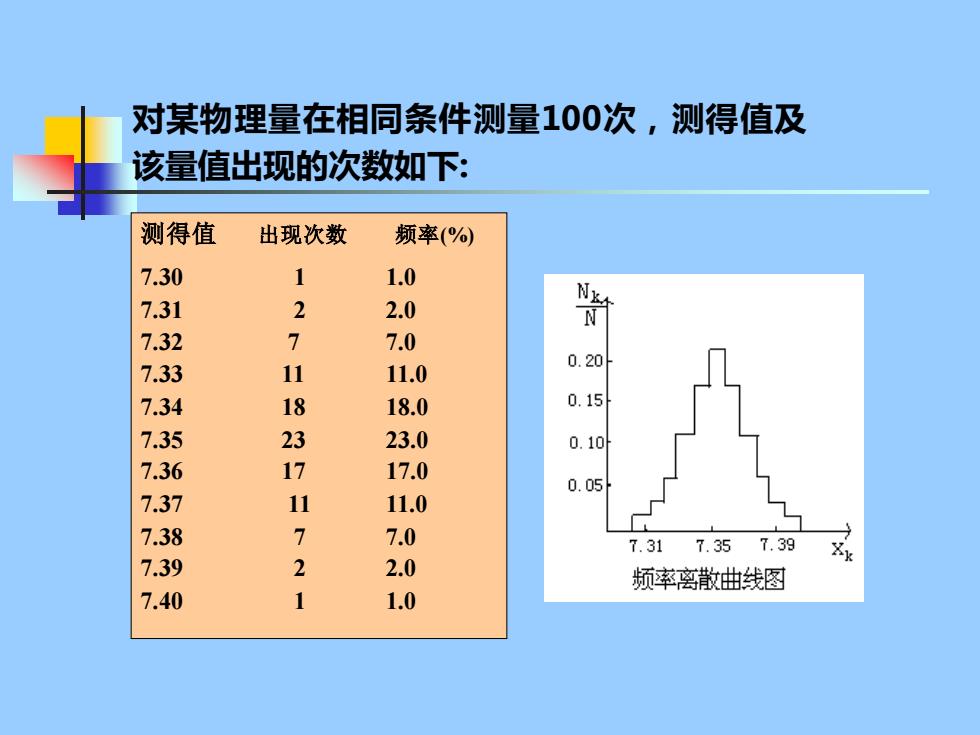
对某物理量在相同条件测量100次,测得值及 该量值出现的次数如下: 测得值 出现次数 频率(% 7.30 1 1.0 7.31 2 2.0 的 7.32 7 7.0 7.33 11 0.20 11.0 7.34 18 18.0 0.15 7.35 23 23.0 0.10 7.36 17 17.0 0.05 7.37 11 11.0 7.38 7 7.0 7.31 7.35 7.39 7.39 2.0 4 2 频率离散曲线图 7.40 1 1.0
对某物理量在相同条件测量100次,测得值及 该量值出现的次数如下: 测得值 出现次数 频率(%) 7.30 1 1.0 7.31 2 2.0 7.32 7 7.0 7.33 11 11.0 7.34 18 18.0 7.35 23 23.0 7.36 17 17.0 7.37 11 11.0 7.38 7 7.0 7.39 2 2.0 7.40 1 1.0
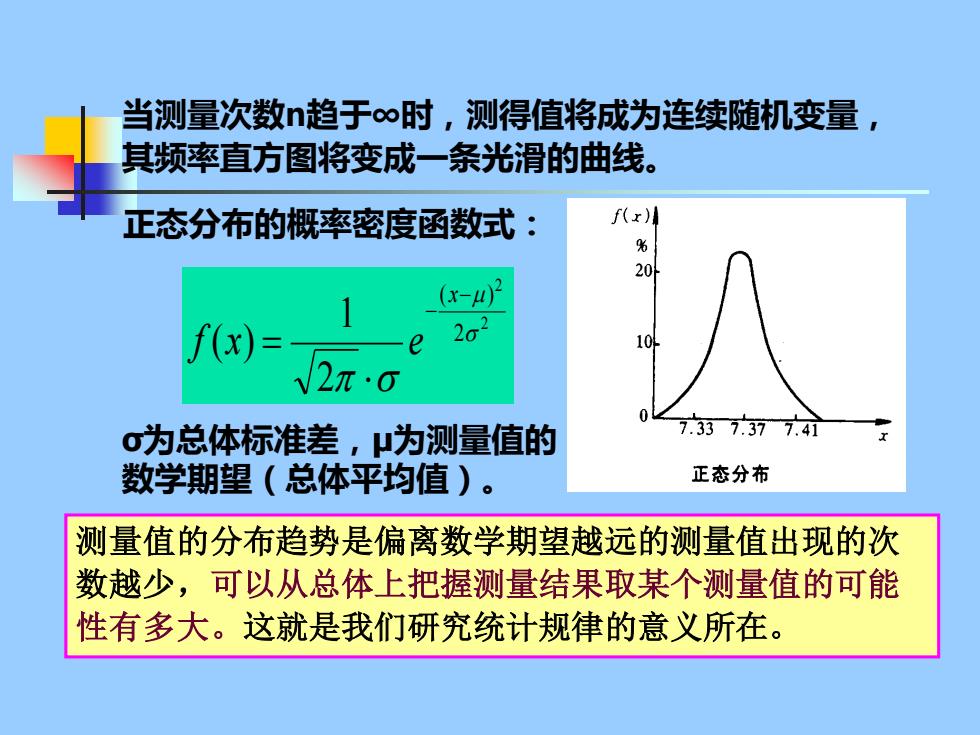
当测量次数趋于∞时,测得值将成为连续随机变量, 其频率直方图将变成一条光滑的曲线。 正态分布的概率密度函数式: f(z) % 20 (x-2 f(x) 202 σ为总体标准差,μ为测量值的 .337.377.4i 数学期望(总体平均值)。 正态分布 测量值的分布趋势是偏离数学期望越远的测量值出现的次 数越少,可以从总体上把握测量结果取某个测量值的可能 性有多大。这就是我们研究统计规律的意义所在
2 2 2 ( ) 2 1 ( ) − − = x f x e 正态分布的概率密度函数式: 当测量次数n趋于∞时,测得值将成为连续随机变量, 其频率直方图将变成一条光滑的曲线。 σ为总体标准差,μ为测量值的 数学期望(总体平均值)。 测量值的分布趋势是偏离数学期望越远的测量值出现的次 数越少,可以从总体上把握测量结果取某个测量值的可能 性有多大。这就是我们研究统计规律的意义所在