
对比参数反映了气体所处状态偏离临界点的倍数。三个量的量纲均为一。注意 对比温度必须使用热力学温度 范德华指出,当不同气体有两个对比参数相等时,第三个对比参数也将(大 致)相等。这即是对应状态原理。人们把具有相同对比参数的气体称为处于相 同的对应状态。对应状态原理对球形分子组成的气体最为适用,对非球形或极 性分子组成的气体有时会有较大偏差。 3.普遍化压缩因子图 把对比参数的表达式(1.5.4)引入压缩因子的定义式(1.5.1c),并结合式 (1.5.3)可得 (1.5.5) 因实验表明,大多数气体的临界压缩因子Z在0,26一0.29的范围内,可近似作 为常数处理,所以上式说明无论气体各自的性质如何,处在相同的对应状态时 不同气体将具有相同的压缩因子。换句话说,也就是当不同气体处在偏离临界 状态相同倍数的状态时,它们偏离理想气体的程度也相同。对于一定量的气体 来说,因pVT三个变量中只有两个是独立变量,所以对比参数p,、V.、T,中也只有 两个是独立变量,因此可以将乙表示成为两个对比参数的函数。通常选P,、T,为 变量 Z=f(p,,T.) (1.5.6) 荷根(Hongen0A)及华德生(Watson K M)在20世纪40年代用若干种无 机、有机气体实验数据的平均值,描绘出图1.5.1的等T,线,表达了式(1.5.6) 的普遍化关系,称为双参数普遍化压缩因子图。由于不同气体的Z。有一定的差 别,尤其是像水蒸气、氨气这类强极性分子组成的气体,所以将普遍化压缩因子 图用于各种气体时,由图中查到的压缩因子有时准确性并不高,不过通常可满足 工业上的应用,具有一定的方便性。但在需要精确计算气体pVT关系时,还是 应该使用各自气体的压缩因子。 由图1.5.1可知,在任何T,下,当P,一0时,2→1;而在P相同时,T越大,Z 偏离1的程度越小,这说明低压高温气体更接近理想气体。T,<1时,Z-P,曲线 均中断于某一P,点,这是因为T<1的真实气体在升压到饱和蒸气压时会发生液 化。在T≥1但不太高时,大多数Z-P,曲线随P,的增加先下降后上升,经历一个 最低点。这反映出真实气体在加压过程中从开始的较易压缩转变到后来的较难 压缩的情况,其原因如§1.4.1中所述。 普遍化压缩因子图具有一定的实用价值,因为只要知道了真实气体所处的 状态及临界参数,即可从图上查出Z值,然后通过式(1.5.1b)V=ZRT对真实 16
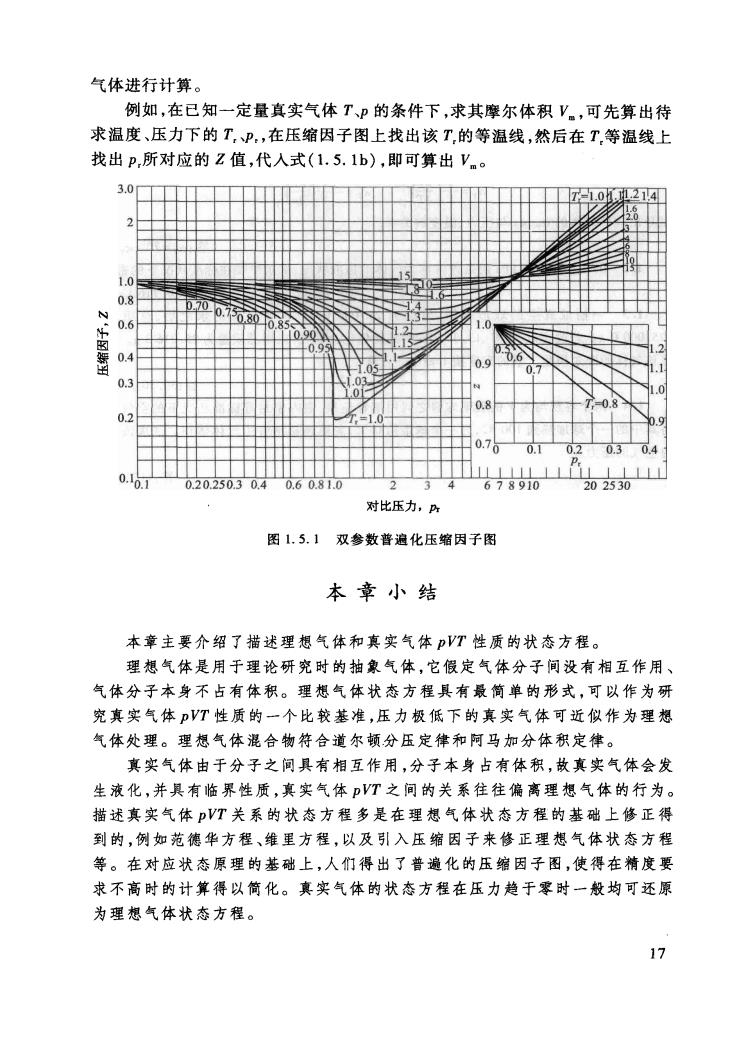
气体进行计算。 例如,在已知一定量真实气体TP的条件下,求其摩尔体积V。,可先算出待 求温度、压力下的T,P,在压缩因子图上找出该T的等温线,然后在T等温线上 找出p,所对应的Z值,代人式(1.5.1b),即可算出V.。 300 06 0.4 0.3 00.1 03 202530 对比压力,序 图15.1双参数普遍化压缩因子图 本章小结 本章主要介绍了描述理想气体和真实气体VT性质的状态方程。 理想气体是用于理论研究时的抽象气体,它假定气体分子间没有相互作用 气体分子本身不占有体积。理想气体状态方程具有最筒单的形式,可以作为研 究真实气体VT性质的一个比较基准,压力极低下的真实气体可近似作为理想 气体处理。理想气体混合物符合道尔顿分压定律和阿马加分体积定律。 真实气体由于分子之问具有相互作用,分子本身占有体积,故真实气体会发 生液化,并具有临界性质,真实气体VT之间的关系往往偏离理想气体的行为。 描述真实气体VT关系的状态方程多是在理想气体状态方程的基础上修正得 到的,例如范德华方程、维里方程,以及引入压缩因子来修正理想气体状态方程 等。在对应状态原理的基础上,人们得出了普遍化的压缩因子图,使得在精度要 求不高时的计算得以简化。真实气体的状态方程在压力趋于零时一般均可还原 为理想气体状态方程 17

少 题 1.1物质的体影胀系数&,与等温压缩率K,的定义如下: ,(韵 ,=-(的 试导出理想气体的a¥、K,与压力、温度的关系。 答:av=TK,p 1.20℃、101.325kPa的条件常称为气体的标准状况,试求甲烷在标准状况下的密度。 答:0.716kgm 1.3一抽成直空的球形容器,质量为25.0000g。充以4℃的水之后,总质量为 125.0000g。若改充以25℃、13.33kPa的某碳氢化合物气体,则总质量为25.0163g。试估 算该气体的摩尔质量。水的密度按1gcm'计算。 答:30.30gmol 1,4两个容积均为V的玻璃球泡之间用细管连接,泡内密封着标准状况下的空气。若 将其中的一个球加热到00℃,另一个球维持0℃,忽略连接细管中气体体积。试求该容器 内空气的压力。 答:117.0kPa 1.50℃时氯甲烷(CH,C)气体的密度p随压力的变化如下: p/kTa 101.325 67.550 50.663 33.775 25.331 p/(g.dm) 2.3074 1.5263 1.14010.75713 0.56660 试作号-p图,用外推法求CH,C的相对分子质量。 答:50.50 1.6今有20℃的乙烷-丁烷混合气体,充人一抽成真空的200cm'容器中,直至压力达 到101.325kPa,测得容器中混合气体的质量为0.3897g。试求该混合气体中两种组分的摩 尔分数及分压力。 答:yz=0.401;yT=0.599;pPz=40.63kPa:pr=60.70kPa 1.7如图所示,一带隔板的容器中,两侧分别有同温度、不同压力的H,与N,p(H)= 20kPa,p(N2)=10kPa,二者均可视为理想气体。 H2 3 dm' N2 1 dm' p(H2) p(N2)T (1)保持容器内温度恒定,抽去隔板,且隔板本身的体积可忽略不计,试计算两种气体混 合后的压力:

(2)计算混合气体中H,和N的分压力: (3)计算混合气体中H和N,的分体积。 答:(1)17.5kPa;(2)l5.0kPa,2.5kPa:(3)3.43dm':0.57dm 1,8乙烯、氯化氢及乙烯构成的混合气体中,各组分的摩尔分数分别为0.89.0.09及 0.02。在恒定压力101.325kPa下,用水吸收掉其中的氯化氯气体后所得混合气体中增加了 分压为2.670kPa的水蒸气。试求洗涤后混合气体中氯乙烯和乙烯的分压力。 答.96.487kPa:2.168kPa 1.9室温下一高压釜内有常压的空气,为确保实验安全进行需采用同样温度的纯氮进 行置换,步骤如下:向釜内通氮气直到4倍于空气的压力,然后将釜内混合气体排出直至恢复 常压。重复三次。求签内最后排气至常压时,该空气中氧的摩尔分数。设空气中氧、氮摩尔 分数之比为14 答:3.13×10 1.1025℃时饱和了水蒸气的湿乙炔气体(即该混合气体中水蒸气分压力为同温度下 水的饱和蒸气压)总压力为138.7kP,干恒定总压下冷却到10℃,使部分水蒸气凝结为水。 试求每摩尔干乙炔气在该冷却过程中凝结出水的物质的量。已知25℃及10℃时水的饱和 蒸气压分别为3.17kPa及1.23kPa 答:0.01444mo1 1.11有某温度下的2dm3湿空气,其压力为101.325kPa,相对湿度为60%。设空气中 0与N,的体积分数分别为0.21与0.79,求水蒸气,0,与N,的分体积。已知该温度下水的饱 和蒸气压为20.55kPa(相对湿度即该温度下水蒸气的分压与水的饱和蒸气压之比)。 答:V(H,0)=0.2434dm':(0,)=0.3688dm':V(N,)=1.3878dm 1.12 一密闭刚性容器中充满了空气,并有少量的水存在。当容器在300K条件下达平 衡时,容器内压力为101,325kPa。若把该容器移至373.15K的沸水中,试求容器中达到新 的平衡时应有的压力。设容器中始终有水存在,且可忽略水的体积的任何变化。已知300K 时水的饱和蒸气压为3.567kPa。 答:222.92kPa 1.13C0,气体在40℃时的摩尔体积为0.381dm·mol'。设C0,为范德华气体,试求 其压力,并比较与实验值5066.3kPa的相对误差 答:5187.7kPa:2.4% ·1.14今有0℃、40530kPa的N,气体,分别用理想气体状态方程及范德华方程计算其 摩尔体积。实验值为0.0703dmm。 答:0.0560dmmo'0.0731dm3mol ·1:15试由被义尔温度T的定义式,证明范德华气体的T可表示为 T.-bR 式中a,b为范德华常数。 1.16把25℃的氧气充入40dm'的氧气钢瓶中,压力达202.7×102kPa。试用普遍化压 缩因子图求钢瓶中氧气的质量。 答:11,02kg 19

·1.17已知298.15K时,乙烷的第二、第三维里系数分别为B=-186×10·m·mol和 C=1.06×10m2·m0l',试分别用维里方程和普遍化压缩因子图计算28.8g乙烷气体在 298.15K,1×103m容器中的压力值,并与用理想气体状态方程计算的压力值进行比较。 答:Pe里=1.974×103kPa:P1wr=1.949×10'kPa;Pm=2.374×103kPa