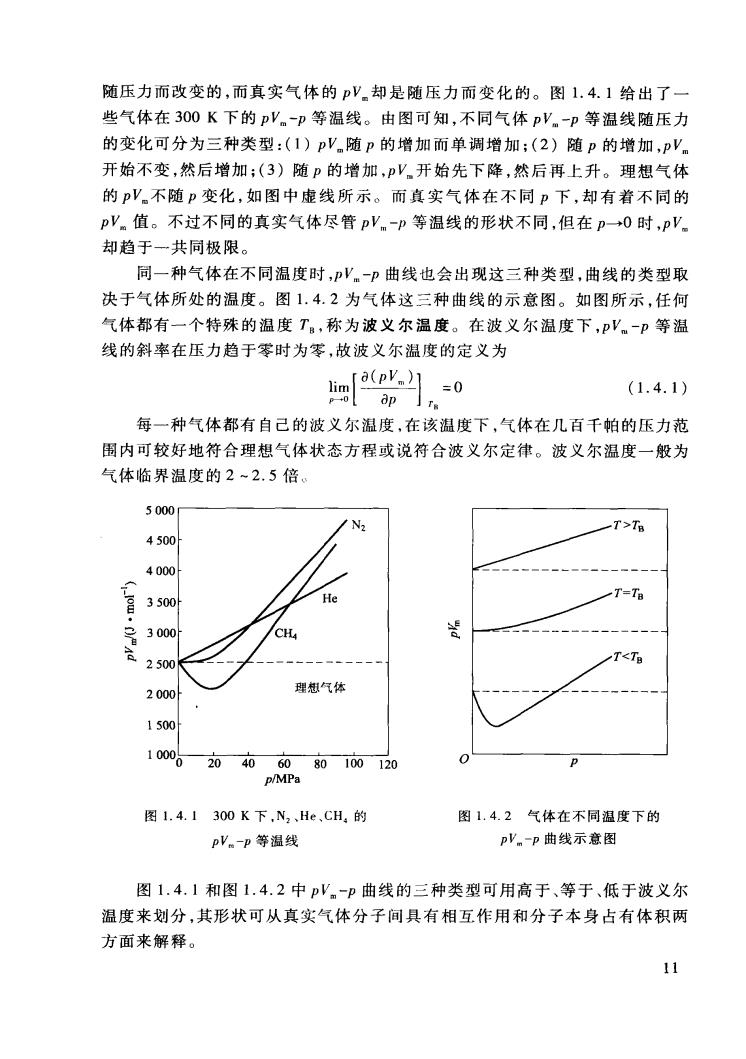
随压力而改变的,而真实气体的pV却是随压力而变化的。图1.4.1给出了一 些气体在300K下的pV。-p等温线。由图可知,不同气体pV。-p等温线随压力 的变化可分为三种类型:(1)pV随p的增加而单调增加;(2)随p的增加,pV。 开始不变,然后增加;(3)随P的增加,PV开始先下降,然后再上升。理想气体 的pV.不随p变化,如图中虚线所示。而真实气体在不同p下,却有着不同的 pV值。不过不同的真实气体尽管pV。-p等温线的形状不同,但在p→0时,pV 却趋于一共同极限。 同一种气体在不同温度时,V.-p曲线也会出现这三种类型,曲线的类型取 决于气体所处的温度。图1.4.2为气体这三种曲线的示意图。如图所示,任何 气体都有一个特殊的温度T。,称为波义尔温度。在波义尔温度下,P'。-p等温 线的斜率在压力趋于零时为零,故波义尔温度的定义为 =[g91n0 (1.4.1) 每一种气体都有自己的波义尔温度,在该温度下,气体在几百千帕的压力范 围内可较好地符合理想气体状态方程或说符合波义尔定律。波义尔温度一般为 气体临界温度的2~2.5倍。 5000 4500 4000 -T 3500 He 300 CH A 2500 "<T 2000 理想气体 1500 100002040608010120 p/MPa 图1.4.1300K下,N2,He,CH,的 图1.4.2气体在不同温度下的 pV。-p等温线 pV。-p曲线示意图 图1.4.1和图1.4.2中pV。-p曲线的三种类型可用高于、等于、低于波义尔 温度来划分,其形状可从真实气体分子间具有相互作用和分子本身占有体积两 方面来解释

如前所述,压力是由于气体分子运动时碰撞器壁所产生的结果。理想气体 的压力是气体分子间无相互作用条件下的压力。对于真实气体,由§1.1可知 分子间一般存在相互吸引作用。处于容器内部的气体分子由于受到来自四面八 方的吸引,总的结果使引力的作用相互抵消,合力为零。而靠近器壁的气体分 子,因只受到内部分子的吸引,故合力不为零,总的结果使分子受到一个将其拉 向内部的引力。这种向内的引力减弱了气体分子对器壁碰撞的冲量,使得真实 气体的V与理想气体相比趋向于减小。另一方面,由于真实气体分子本身占 具体积,气体的V不再是1mol分子自由活动的空间,而是自由活动空间加上分 子本身所占的不可压缩空间。压力越高,分子本身所占体积引起的不可压缩性 越大,使得真实气体与理想气体相比p'趋于增大。由此可知,真实气体的p' 随的变化是受两个相反因素制约的。由于温度对这两种因素的影响不一样, 所以有三种类型的pV。-p曲线出现。在T<T时,随着压力由小到大,开始是分 子间引力起主要作用,而后是体积效应起主导作用,故pV随p的变化在经历一 最小值后,随P的增加而增加;在T=T时,开始时两种作用相等,故相互抵消,而 后体积效应起主导作用,故pV。-P曲线开始有一水平过渡,然后随压力上升而 上升;在T>T时,始终是体积效应起主导作用,因此pV随P的增加从一开始就 呈上升趋势。 不同气体具有不同的波义尔温度,所以在某一相同温度下,不同气体会表现 出不同的pVm-p曲线,如图1.4.1所示。 2.范德华方程 真实气体的状态方程一般可分为两类:一类是有一定物理模型的半经验方 程,其中最有代表性的是范德华方程:另一类是纯经验公式,其中最有代表性的 是维里方程。下面先介绍范德华方程。 1873年荷兰科学家范德华(van der Waals)从理想气体与真实气体的差别 出发,用硬球模型来处理真实气体,提出了用压力修正项(α/V)、体积修正项b 来修正压力和体积的思想,导出了适于中低压力下的真实气体状态方程。范德 华认为理想气体的压力是指分子间无相互作用力时的压力,摩尔体积是1ml 气体分子自由活动的空间:而真实气体处在实际的P、V。、T条件时,由于分子间 有相互作用,压力P实际上是理想气体在同等T、'时所应有的压力减去由于内 部吸引力造成的压力减小后的结果,即p=(Pm-a/):而体积在考虑了分子本 身占有的体积b后,自由活动的空间V。,自幽应是(V。-b)。他将修正后的压力、体 积项代入理想气体状态方程P理V。.幽=RT,得到 (p*+同(V.-=RT (1.4.2a) 12

这即是著名的范德华方程。将V。=V/代人上式,经整理可得到适用于气体物 质的量为n的范德华方程: (+9(v-=nT (1.4.2b) 式中,a、b称为范德华常数。某些气体的范德华常数见附录七。 压力修正项(a/)又称为内压力,说明分子间相互吸引力对压力的影响反 比于V,也就是反比于分子间距离,的6次方。ā是与气体种类有关的一种特 性常数。一般说来,分子间引力越大,则a值越大。a的单位是Pa·m°·mol2。 范德华还认为,常数只与气体种类有关,与温度条件无关。 体积修正项表示每摩尔真实气体因分子本身占有体积而使分子自由活动 空间减小的数值。显然,常数6应与气体的性质有关,也是物质的一种特性常 数。b的单位是m3·mol。范德华还曾按照硬球模型,进-一步导出b是1mo硬 球气体分子本身体积的4倍,范德华认为常数b也应与气体的温度无关。 真实气体当压力p→0时,V.→,此时范德华方程中(p+a/V)及(V。-b) 两项分别化为p及'。,范德华方程还原为理想气体状态方程。 如果用范德华方程来计算真实气体的P-V等温线,可发现在临界温度以上 时,计算结果与实际符合较好,但在临界温度以下的气-液两相共存区有较大差 别。由范德华方程算出的P-V等温线在该区城内出现一个极大值和一个极小 值,如图1.3.2中g,V,V;l,的S形虚线所示,这是与实际的水平线段不相符的。 随温度升高,算出的极大值与极小值逐渐靠近,最后至临界温度T时,两点汇聚 成T曲线上的拐点c,即临界点。不过S形曲线中g,V,线和l?线分别有着过 饱和蒸气和过热液体的含义, 3.维里方程 维里一词来源于拉丁文vial,是“力"的意思。维里方程是卡莫林·昂尼斯 (Kammerlingh Onnes)于20世纪初作为纯经验方程提出的,一般有两种形式: PV=RT(1+Bp+Cp2+Dp'+..) (1.4.3) p.g是* (1.4.4) 式中,B、C、D、…与B’、C、D'、…分别称为第二、第三、第四、…维里系数,它们 都是温度T的函数,并与气体的本性有关。两式中的维里系数有不同的数值和 单位,其值通常由实验的pVT数据拟合得出。当压力p→0,体积V。→∞时,维里 方程还原为理想气体状态方程。虽然维里方程表示成无穷级数的形式,但实际 上通常只用最前面的几项进行计算。在计算精度要求不高时,有时只用到第二 项即可,所以第二维里系数较其他维里系数更为重要。 13

维里方程最初虽然完全是一个经验方程,但后来从统计力学的角度得到了 证明,所以维里方程已由原来的纯经验式发展为具有一定理论意义的方程。第 二维里系数反映了两个气体分子间的相互作用对气体VT关系的影响,第三维 里系数则反映了三分子相互作用引起的偏差。因此,通过由宏观pVT性质测定 拟合出的维里系数,可建立起宏观VT性质与微观领域势能函数之间的联系。 §1.5对应状态原理及普遍化压缩因子图 理想气体状态方程是一个不涉及各种气体各自特性的普遍化方程。真实气 体状态方程中常含有与气体种类有关的特性常数,如范德华常数等。能否导出 一个普遍适用的真实气体状态方程,这一直是从事工程计算的人们颇感兴趣的 课题,而对应状态原理在这方面给了人们很大的启示。 1.压缩因子 描述真实气体T关系的状态方程中,最直接、最准确、形式最简单、适用 的压力范围也最广泛的,是将理想气体状态方程用压缩因子Z来加以修正,即 DV=ZRRT (1.5.1a) pV=ZRT (1.5.1b) 由此可知,压缩因子的定义为 z-der pv (1.5.1c) 压缩因子的量纲为一。压缩因子Z并不是一个常数,而是T、P的函数。测量真 实气体在不同温度、压力下的pVT数据,可由式(1.5.1c)算得压缩因子。许多 气体在不同条件下的压缩因子或VT数据可由手册或文献查到。由于压缩因 子是由实验测量得到的,没有引入任何假设,所以往往具有较高的准确性。 式(1.5.1c)中的V为真实气体在p、T条件下的摩尔体积,而理想气体在同 样p、T下具有的摩尔体积V(理想)=RT/p,代人式(1.5.1c)可有 V(真实) Z=V.(理想) (1.5.2) 式(1.5.2)表明,当Z<1时,真实气体的摩尔体积比相同条件下理想气体的要 小,说明真实气体比理想气体易于压缩:反之,Z>1时,真实气体的摩尔体积比 相同条件下理想气体的要大,说明真实气体比理想气体难于压缩;而对于理想气 体,Z=1。由于Z的大小反映出真实气体比理想气体压缩的难易程度,所以将 它称为压缩因子。 14

根据压缩因子定义式(1.5.1c),对比维里方程的式(1.4.3)和式(1.4.4)可 知,维里方程实际上是将压缩因子Z表示成p或V的级数关系,即 Z=l+Bp+Cp2+Dp3+… 由上式可知当温度一定时压缩因子Z可表示为压力P的函数,人们有时也 用Z-图来表示真实气体对理想气体的偏差随压力变化的情况。而任何气体 在p0时,Z一→1。显而易见Z-p图的形状与前面pV.p图的形状是对应的,这 里就不再详细叙述。 真实气体的压缩因子在计算精度要求不太高时可用下面将要介绍的压缩因 子图的方法来求。在精确计算时,则需通过实测的真实气体的pVT数据,然后 由定义式(1.5.1c)来求算。值得一提的是,以前受技术条件的制约,气体的pVT 数据多是中低压范围的。随着科学技术的进步,测量几十甚至几百兆帕下气体 的pVT数据已不是难事。所以现在有许多气体在高压下的pVT数据可以从手 册或文献中查到。实际工作中,可根据需要查出某气体的pVT数据,算出某一 温度下的2-关系,画图或用计算机关联,然后求出工作压力下Z的数值,代人 式(1.5.1a)来计算真实气体的pVT数值。在压力变化较大的情况下,计算机关 联可采用分段进行的方法,以提高关联精度。 将气体的临界参数代人2的定义式,可得出临界压缩因子Z: RT. (1.5.3) 将实际各气体的P.、V。、T.代入上式计算得到的Z.值大多在0.26-0.29的范 围内,见附录六。 以上结果暗示了气体的临界压缩因子Z。大体上是一个与气体性质无关的 常数,这说明各种气体在临界状态下的性质具有一定的普遍规律,这为以后在工 程计算中建立一些普遍化的pVT经验关系莫定了一定的基础。 2.对应状态原理 真实气体种类不同时,分子之间相互作用不同,因此VT关系中的修正项 不同,临界参数也不同。但各种气体却有一个共同的性质,即在各自临界点处的 饱和蒸气与饱和液体无区别。以临界参数为基准,将气体的P、V。、T除以各自 的临界参数,则有 P,= V.=V... T.=T (1.5.4) P. ,、V、T分别称为对比压力、对比体积和对比温度,又统称为气体的对比参数。 15