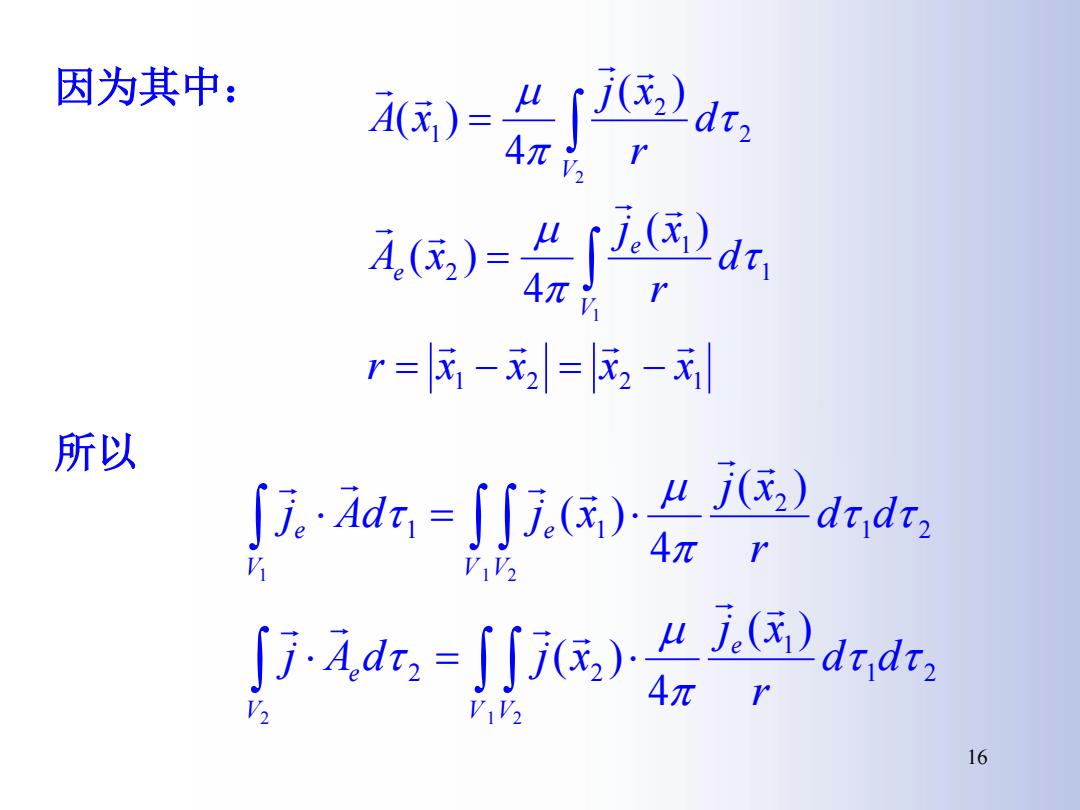
因为其中: 台产a 14 r=民-3=民2- 所以 -d=j小元.底)么jd 4元 r VIV2 jiad=jfj0深,)drd, VIV 4πr 16
因为其中: 所以 1 2 2 1 1 1 2 2 2 1 1 2 ( ) 4 ( ) ( ) 4 ( ) r x x x x d r j x A x d r j x A x V e e V 2 1 2 1 1 2 1 2 1 2 2 1 2 2 1 1 ( ) 4 ( ) ( ) 4 ( ) V V e V e V V e V e d d r j x j A d j x d d r j x j Ad j x 16

该两式相等,因此电流方在外场A中的相互作用能量 为 W,=∫jA 5、举例讨论用A计算 [例1无穷长直导线载电流工,求空间的矢势A和磁场 B。 Solution d 取导线沿z轴,设p点 N 到导线的垂直距离为R,电 流元Idz到p点距离为VR'+z2 17
该两式相等,因此电流 在外场 中的相互作用能量 为 5、举例讨论用 计算 [例1]无穷长直导线载电流I,求空间的矢势 和磁场 。 Solution : 取导线沿z轴,设p点 到导线的垂直距离为R,电 流元Idz到p点距离为 Ae j V i e W j A dv B A A o z dz R P ↑I 2 2 R z 17

因此得到 月= Idz R2+ ne+NF+R)儿 4π 积分结果是无穷大(发散的)。计算两点的矢势差值 可以免除发散,若取R点的矢势值为零,则 4(p)-A.(po)=lim 以n+E2+R M四4元:+VE2+R M lim e-+ 4红1+V1+R6/M2-1+1+R2/M2 18
因此得到 积分结果是无穷大(发散的)。计算两点的矢势差值 可以免除发散,若取R0点的矢势值为零,则 ln( ) 4 4 2 2 2 2 z z R I R z Idz Az 2 2 2 2 0 2 2 0 2 2 2 0 2 2 2 0 1 1 1 1 1 1 1 1 l n 4 lim l n 4 ( ) ( ) lim R M R M R M I R M z z R I z z R A p A p M M M M z z 18

每项相乘后,再二次项展开得 lim in 4M2 M-→0 4π 1 RoR2 R*4 M l W W R R2- In 4π 2π R 2π R 亦即 p)-,)=- R 2π R 故 A(p)=- R In R b 2元 19
每项相乘后,再二次项展开得 亦即 故 0 0 2 2 0 2 2 2 2 0 2 2 2 2 0 0 ln 2 ln 2 ln 4 4 1 4 1 ln 4 lim R I R R I R R I R M R R R M R R R I M z e R I R A p A p 0 0 ln 2 ( ) ( ) z e R I R A p 0 ln 2 ( ) 0 19

取4的旋度,得到 B=xA=-Vx×L1 R 2π Ro R 0 ye.-vIn xe. 2π Ro R =-V In xe. 2π Ro =-V (lnR-lnRo)×e: 2元 2πR /0X0,=22Xi∂ 2元R 2πR 结果与电磁学求解一致。 20
取 A 的旋度,得到 2 1 2 (ln l n ) 2 l n 2 l n 2 l n 2 l n 2 0 0 0 0 0 R z z R z z z z z e e R I e e R I R R e I e R I R e R I R e R I R e R I R B A 2 e R I 结果与电磁学求解一致。 20