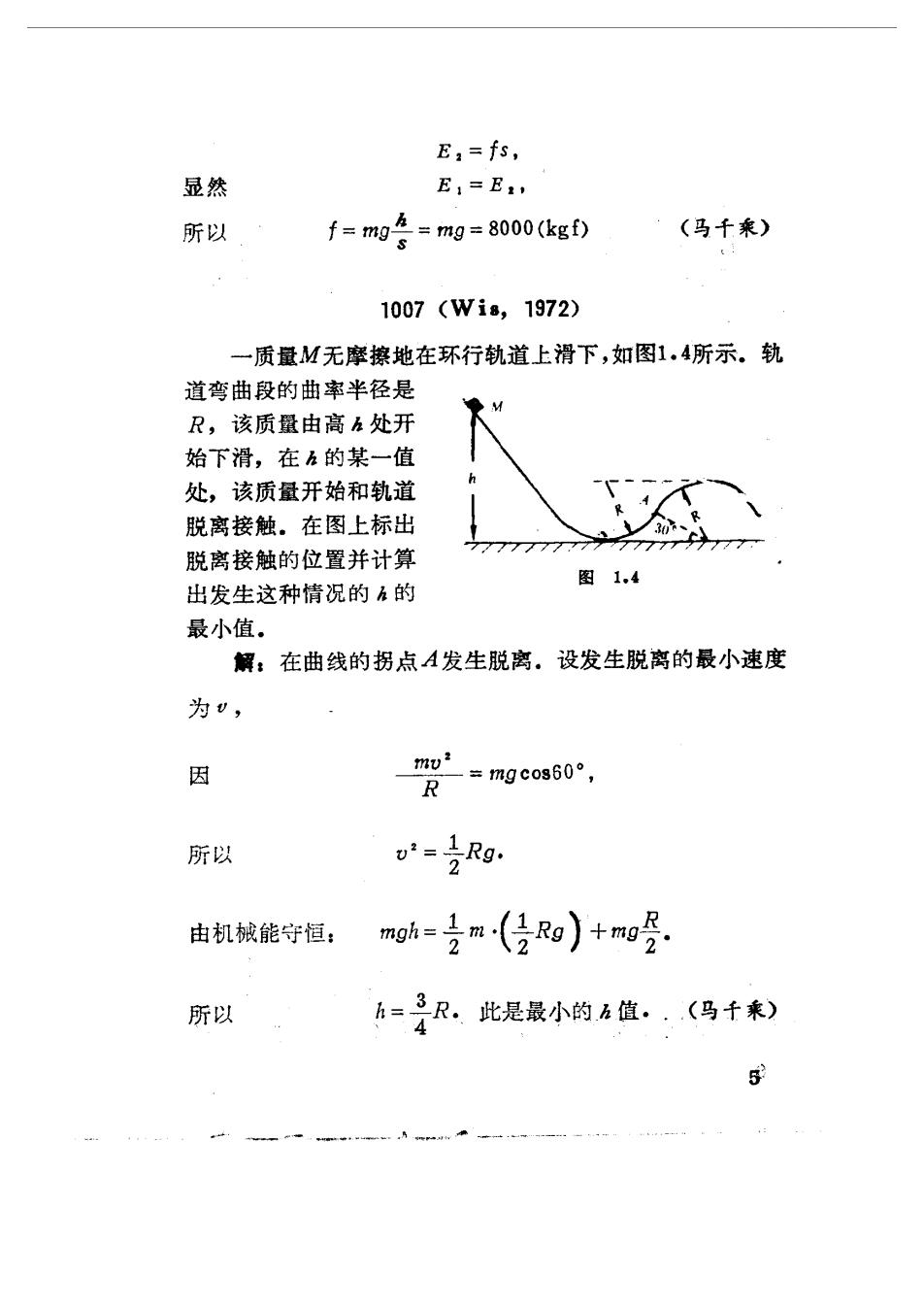
E,=fs, 显然 E,=E, 所以 f=mg=mg=8000(kgf) (马千来) 1007(Wi8,1972) 一质量M无摩擦地在环行轨道上滑下,如图1.4所示。轨 道弯曲段的曲率半径是 R,该质量由高h处开 始下滑,在的某一值 处,该质量开始和轨道 脱离接触。在图上标出 脱离接触的位置并计算 77777 出发生这种情况的的 图1.4 最小值。 解:在曲线的拐点A发生脱离。设发生脱离的最小速度 为”, ® mo: =mgco360°, 所以 。2=是Rg: 由机械能守恒: moi=是m(侵Rg)+mo受. 所以 A=星R此是最小的么值.,(马千乘)

1008(Wi8,1972) 考虑一个转动的球形行星,该行星赤道上某点的速度是 V,行星转动的效果是使赤道上的g是极点上g的一半。问 该行星极点上一粒子的逃逸速度等于多少?用V乘上某个因 子表示。 解:若分别以g和g'表示极点和赤道上的加速度,则 在极点: 所以 GM=gR*. kmg'nggng 在赤道:m 所以 9、2g R· 在此行星极点上的一个粒子,若想要越出行星的引力 范围,取无穷远处引力势能为零,则它的机械能至少应等 于零 2m16-0, R 所以 0·=2GM=2gR R R=2gR=4 RR=4V, v=2",因此,其逃逸速度是2V. (马千乘) 1009(Wis,1973) 一小质量m放在一半径为R的水平圆盘边上,此小质量 和圆盘之间的静摩擦系数为“,若圆盘绕其轴以某一角速度 旋转而使得小质量滑出圆盘并落到下面h(m)的地板上。问 6

从它离开圆盘的那一点算起,小质量所越过的水平距离等于 多少? 解:质点圆盘上的最大静摩擦力f=4mg,当质点由圆 盘上滑出时,它的水平速度v是: n R=μmg, 所以 u=V√4Rg. 下落高度所用的时间: √西 因此在落地前,水平方向越过的距离: S=vt=√2μRh. (马千乘) 1010(Wi8,1980) 一弹子球以一种正规的方式由阶梯上弹下,它击在每一 步阶梯的同一个位置,并且在每一步阶梯上弹起相同的高度。 该阶梯的高度等于它的宽度(阶宽等于阶 高)而且恢复系数e已知。求弹子球所必 需的水平速度和弹起的高度。(恢复系数 e被定义为e=-,/u,其中v1和: 为弹起后和弹起前的速度) 解:如图1.5,取坐标系, 图1.5 设水平速度为口 则落地时的速度 01=0st+v:j 弹起时的速度 ",=0i+v1j 由机械能守恒

合m(oi+)=mo+i》+ngl, 其中1设为阶梯的高度. 又因 一v,=ev,于是可求得: =20。 自弹起后,至下一次落地所需时间是: t=g1=g1+e) 在此时间内,弹子球沿水平方向运动的距离是1. 所以 vt=1. =片品。“a。√g 1g /1-e2 √竖. 此即是必需的水平速度. 由机械能守恒,可求出弹起的高度H, 合m=mg, 所以 2gl (马千乘) 1011(Wis,1978) 假设所有的表面均是无摩擦的并且滑轮及绳索的质盘可 以忽略(图1.6)。求在不致于产生m1、m2和M之间的任何
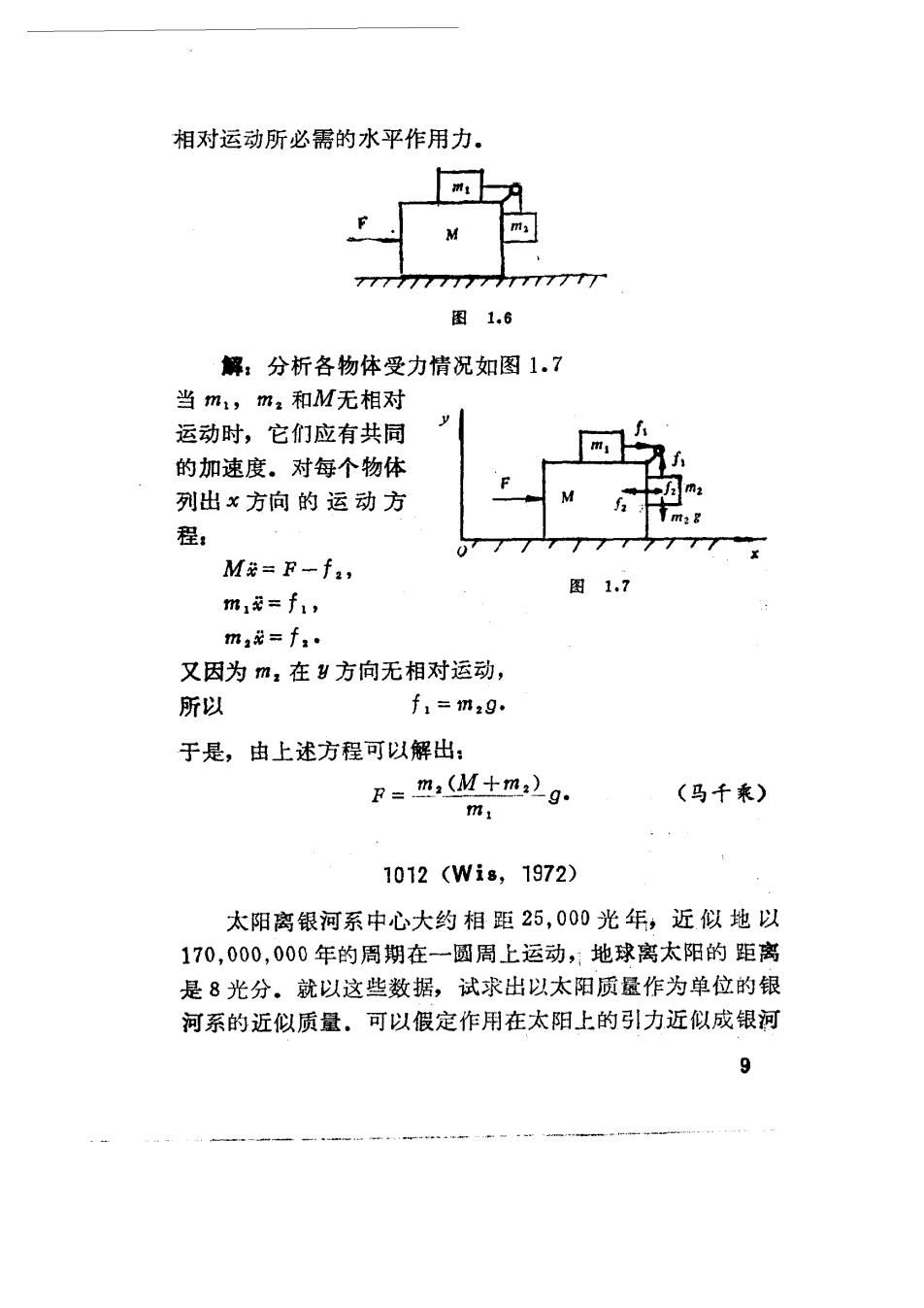
相对运动所必需的水平作用力。 M 图1,6 解:分析各物体受力情况如图1.7 当m1,mz和M无相对 运动时,它们应有共同 的加速度。对每个物体 列出x方向的运动方 程: M=F-f, 图1.7 m,=f, m,花=f,· 又因为m:在y方向无相对运动, 所以 f,=m,9 于是,由上述方程可以解出: B=m,(Mmg. (马千乘) m 1012(Wis,1972) 太阳离银河系中心大约相距25,000光年,近似地以 170,000,000年的周期在一圆周上运动,地球离太阳的距离 是8光分。就以这些数据,试求出以太阳质量作为单位的银 河系的近似质量.可以假定作用在太阳上的引力近似成银河 0