五、; 模糊集合间的包含关系—二包含度定理 1.模糊子集的几何表示 B的所有模糊子集构成集合 模糊幂集F(2),它构成了 在单位超立方体中倚着原点的规则的超长方形,其边宽等于各 隶属度值m(x)。可以用Lebesguei测度或体积V(B)来度量 F(2B)的大小,其中,体积V(B)为隶属度值的乘积: 2z}=(0) X=(11) 23 B V(B)=Πm(x) i=1 F(2) 中=(00) }=(10) 号马 图7.7
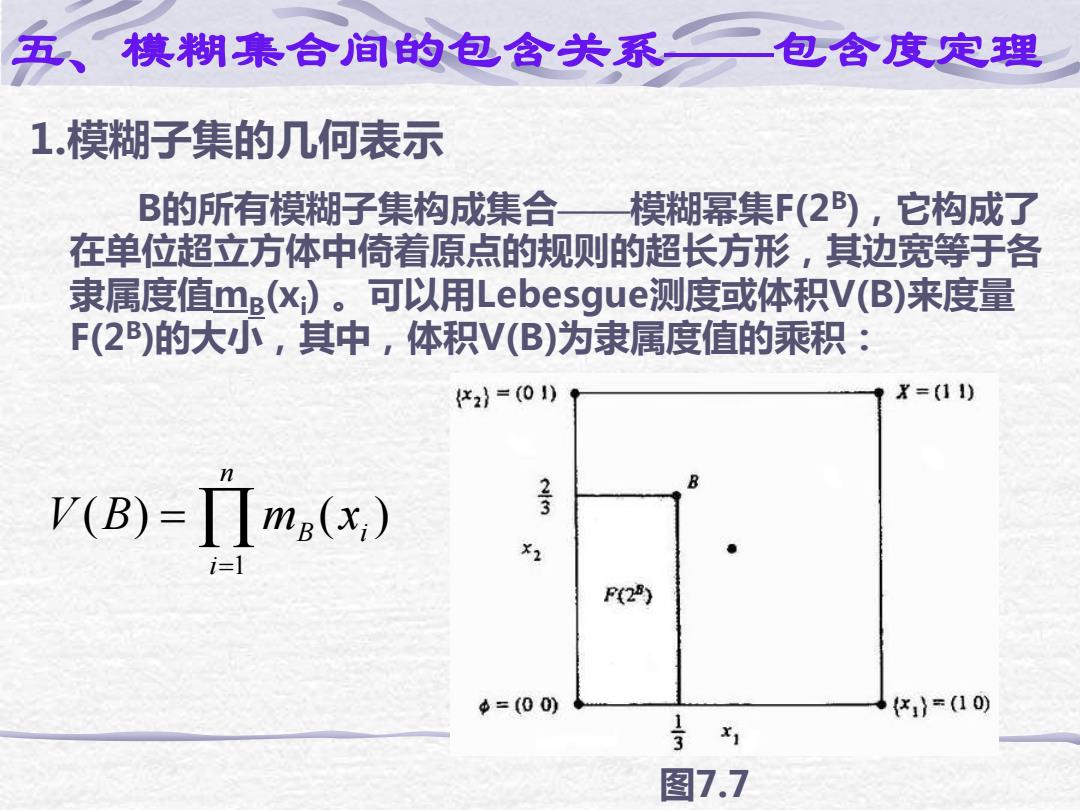
1.模糊子集的几何表示 B的所有模糊子集构成集合——模糊幂集F(2B),它构成了 在单位超立方体中倚着原点的规则的超长方形,其边宽等于各 隶属度值mB(xi ) 。可以用Lebesgue测度或体积V(B)来度量 F(2B)的大小,其中,体积V(B)为隶属度值的乘积: 1 ( ) ( ) n B i i V B m x = = 五、模糊集合间的包含关系——包含度定理 图7.7

五、; 模糊集合间的包含关系—包含度定理 2.包含度定理: 在图7.7中,点A可以是长方形内的点,也可以不是。在长 方形(2)外不同的点A是B的不同程度的子集。而上述二值定 义下的子集性忽略了这一点。考虑到集合A属于F(2)的不同 程度,通过抽象隶属度函数来定义包含度: S(A,B)=Degree(AC B) =mr29,(A) S(,)在[0,1]之间取值,其代表了多值的子集测度(包含 度),是模糊理论中的基本的、标准的结构
2.包含度定理: 在图7.7中,点A可以是长方形内的点,也可以不是。在长 方形F(2B)外不同的点A是B的不同程度的子集。而上述二值定 义下的子集性忽略了这一点。考虑到集合A属于F(2B)的不同 程度,通过抽象隶属度函数来定义包含度: S(.,.)在[0,1]之间取值,其代表了多值的子集测度(包含 度),是模糊理论中的基本的、标准的结构。 (2 ) ( , ) ( ) B ( ) F S A B Degree A B m A = = 五、模糊集合间的包含关系——包含度定理

五、 模糊集合间的包含关系—包含度定理 度量S()的两种方法: (1)代数方法:即失配法(fit-violation strategy) 假定X包含有100个元素:X={x1,x100。而只有第一个 元素违背了主导隶属度函数关系,使得ma(X1)>mB(x1)。直 观上,我们认为A很大程度上是B的子集。可以估算,子集性 为S(A,B)=0.99,并且,如果X包括1兆个元素,A几乎完全 是B的子集了。可见失配的幅度ma(1)-mg(1)越大,失配的 数目相对于模糊集A的大小越多,那么A就越不能算是B的子 集,或者说,A就越象是B的超集。直观上有 SUPERSETHOOD(A.B)-1-S(A,B)
度量S(.,.)的两种方法: (1)代数方法: 即失配法(fit-violation strategy) 假定X包含有100个元素:X={x1 ,…,x100}。而只有第一个 元素违背了主导隶属度函数关系,使得mA(x1 )>mB(x1 )。直 观上,我们认为A很大程度上是B的子集。可以估算,子集性 为S(A,B)=0.99,并且,如果X包括1兆个元素,A几乎完全 是B的子集了。可见失配的幅度mA(x1 )-mB(x1 )越大,失配的 数目相对于模糊集A的大小越多,那么A就越不能算是B的子 集,或者说,A就越象是B的超集。直观上有: SUPERSETHOOD A B S A B ( , ) 1 ( , ) = − 五、模糊集合间的包含关系——包含度定理