物理奥林匹克竞赛：全国物理奥林匹克竞赛第24届复赛试题（含参考答案）

中国科学技术大学物理学院叶邦角整理 从(1)、(2)两式解得的4值便是满足题中条件的最大值，即 10 max (3) V2h 代入有关数据得 4omax =0.71m/s (4) 如果，<omx,小球与平板的碰撞处将不在Q点.设小球第一次刚要与平板碰撞时在竖直方向的速度为， 则有 =2gh (5) 以、分别表示碰撞结束时刻小球和平板沿竖直方向的速度，由于碰撞时间极短，在碰撞过程中，小球和平 板在竖直方向的动量守恒.设小球和平板的质量都是m,则有 01=+m' (6) 因为碰撞是弹性的，且平板是光滑的，由能量守恒可得 m+-+mr+m (7) 解(6)、(7)两式，得 0=0 (8) '=0,=V2gh (9) 碰撞后，平板从其平衡位置以V?为初速度开始作简谐振动.取固定坐标，其原点O与平板处于平衡位置时板的 上表面中点重合，x轴的方向竖直向下，若以小球和平板发生碰撞的时刻作为t=0,则平板在1时刻离开平衡位 置的位移 Xpo =Acos(@t+) (10) 式中 2π 0= (11) A和？是两个待定的常量，利用参考圆方法，在1时刻平板振动的速度 Vpo =-Aosin(ot+p) (12) 因t=0时，xo=0.0o=V”,由(9)、(11)、(12)式可求得 A=27 (13) 2π (14) 把(13)、(14)式代入(10)式，得 (15) 2π 6 中国科学技术大学物理学院叶邦角整理

6 从（1）、（2）两式解得的 0 u 值便是满足题中条件的最大值，即 0 max 2 g u L h  （3） 代入有关数据得 0 max u  0.71m/s （4） 如果 0 0max u u  ，小球与平板的碰撞处将不在 Q 点．设小球第一次刚要与平板碰撞时在竖直方向的速度为 1 v ， 则有 1 v  2gh （5） 以 1 v、V1  分别表示碰撞结束时刻小球和平板沿竖直方向的速度，由于碰撞时间极短，在碰撞过程中，小球和平 板在竖直方向的动量守恒．设小球和平板的质量都是 m，则有 mv = mv 1 1 1    mV （6） 因为碰撞是弹性的，且平板是光滑的，由能量守恒可得 2 2 2 2 2 1 0 1 1 0 1 1 1 1 1 2 2 2 2 2 mv mu = mv mu      mV （7） 解（6）、（7）两式，得 1 v  0 （8） 1 1 V gh  = v  2 （9） 碰撞后，平板从其平衡位置以V1  为初速度开始作简谐振动．取固定坐标，其原点 O 与平板处于平衡位置时板的 上表面中点重合，x 轴的方向竖直向下，若以小球和平板发生碰撞的时刻作为t  0，则平板在 t 时刻离开平衡位 置的位移 x A t PQ   cos   （10） 式中 2π T   （11） A 和 是两个待定的常量，利用参考圆方法，在 t 时刻平板振动的速度   PQ v    A t    sin （12） 因t  0时， PQ x  0 ． vPQ V ，由（9）、（11）、（12）式可求得 2 2 gh A T   （13） π 2    （14） 把（13）、（14）式代入（10）式，得 PQ 2 2π π cos 2π 2 gh x T t T         （15） 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 碰撞后，小球开始作平抛运动.如果第一次碰撞后，小球再经过时间1，与平板发生第二次碰撞且发生在Q处， 则在发生第二次碰撞时，小球的x座标为 x)=28 (16) 平板的x座标为 (17) 2π 在碰撞时，有 xg(2)=xo(52) (18) 由(16)、(17)、(18)式，代入有关数据得 4.90t=4.41cos (19) 这便是t,满足的方程式，通过数值计算法求解方程可得（参见数值列表） 42=0.771s (20) 如果第二次碰撞正好发生在平板的边缘Q处，则有 L=(5+t2) (21) 由(1)、(20)和(21)式得 4,=,L=0.46m5 (22) t+t2 而满足题中要求的的最小值应大于(22)式给出的值.综合以上讨论，4，的取值范围是 0.46m/s<4≤0.71m/s (23) 附：(19)式的数值求解 用数值解法则要代入，不同数值，逐步逼近所求值，列表如下： 0.730 0.750 0.760 0.765 0.770 0.771 0.772 0.775 0.780 0.790 0.810 xno =4.41cos π 3.31 3.12 3.02 2.96 2.91 2.91 2.90 2.86 2.81 2.70 2.48 x。=4.901 2.61 2.76 2.83 2.87 2.91 2.91 2.91 2.94 2.98 3.06 3.21 x阳-x8 0.70 0.36 0.19 0.09 0 -0.01 -0.08 -0.17 -0.36 -0.73 二、参考解答： 解法一 7 中国科学技术大学物理学院叶邦角整理

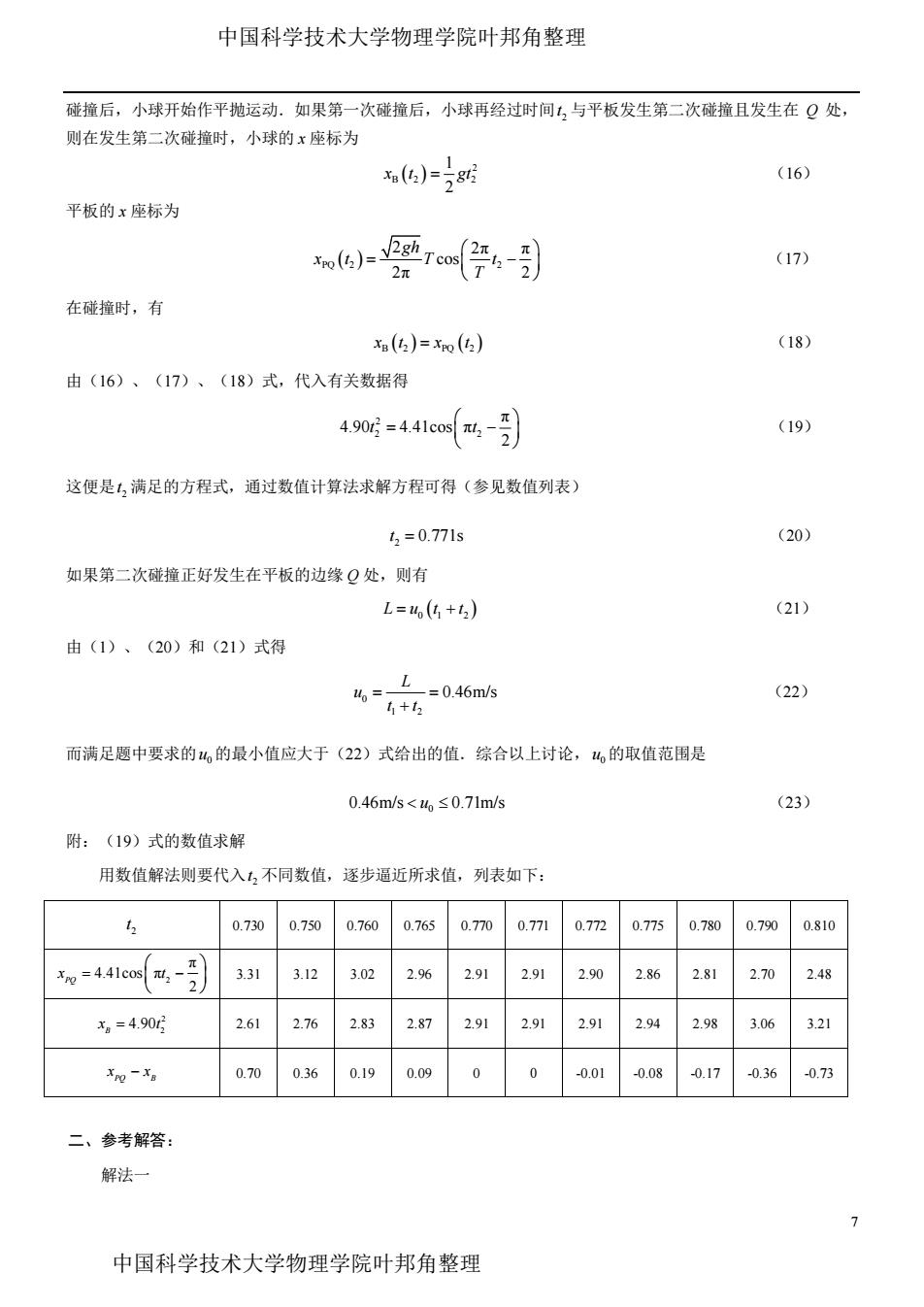
7 碰撞后，小球开始作平抛运动．如果第一次碰撞后，小球再经过时间 2t 与平板发生第二次碰撞且发生在 Q 处， 则在发生第二次碰撞时，小球的 x 座标为   2 B 2 2 1 2 x t gt  （16） 平板的 x 座标为 PQ 2 2   2 2π π cos 2π 2 gh x t T t T         （17） 在碰撞时，有     B 2 PQ 2 x t x t  （18） 由（16）、（17）、（18）式，代入有关数据得 2 2 2 π 4.90 4.41cos π 2 t t         （19） 这便是 2t 满足的方程式，通过数值计算法求解方程可得（参见数值列表） 2t  0.771s （20） 如果第二次碰撞正好发生在平板的边缘 Q 处，则有   L u t t   0 1 2 （21） 由（1）、（20）和（21）式得 0 1 2 0.46m/s L u t t    （22） 而满足题中要求的 0 u 的最小值应大于（22）式给出的值．综合以上讨论， 0 u 的取值范围是 0 0.46m/s 0.71m/s   u （23） 附：（19）式的数值求解 用数值解法则要代入 2t 不同数值，逐步逼近所求值，列表如下： 2t 0.730 0.750 0.760 0.765 0.770 0.771 0.772 0.775 0.780 0.790 0.810 2 π 4.41cos π 2 PQ x t         3.31 3.12 3.02 2.96 2.91 2.91 2.90 2.86 2.81 2.70 2.48 2 2 4.90 B x t  2.61 2.76 2.83 2.87 2.91 2.91 2.91 2.94 2.98 3.06 3.21 PQ B x x  0.70 0.36 0.19 0.09 0 0 -0.01 -0.08 -0.17 -0.36 -0.73 二、参考解答： 解法一 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 因为B点绕A轴作圆周运动，其速度的大小为 0B=01 (1) B点的向心加速度的大小为 ag=021 (2) 因为是匀角速转动，B点的切向加速度为O,故a也是B点的加速度，其方向沿BA方向.因为C点绕D轴作 圆周运动，其速度的大小用c表示，方向垂直于杆CD,在考察的时刻，由图可知，其方向沿杆BC方向.因 BC是刚性杆，所以B点和C点沿BC方向的速度必相等，故有 sπ√2 42o1 0c=0BC0S,= (3) 此时杆CD绕D轴按顺时针方向转动，C点的法向加速度 dcn= (4) CD 由图可知CD=2√21，由(3)、(4)式得 acn= (5) ac 8 B 其方向沿CD方向. 下面来分析C点沿垂直于杆CD方向的加速度，即切向加速度a。.因 为BC是刚性杆，所以C点相对B点的运动只能是绕B的转动，C点相对 B点的速度方向必垂直于杆BC.令vB表示其速度的大小，根据速度合成公式有 UCB =0c-0B 由几何关系得 s=V0g-=2。 -01 (6) 2 2 由于C点绕B作圆周运动，相对B的向心加速度 (7) CB 因为CB=√21，故有 aca= (8) 4 其方向垂直杆CD. 由(2)式及图可知，B点的加速度沿BC杆的分量为 (aa)ac=dg cos (9) 4 所以C点相对A点（或D点）的加速度沿垂直于杆CD方向的分量 do =acn+(aa)nc=0 (10 C点的总加速度为C点绕D点作圆周运动的法向加速度ac.与切向加速度aa的合加速度，即 8 中国科学技术大学物理学院叶邦角整理

8 因为 B 点绕 A 轴作圆周运动，其速度的大小为 B v   l （1） B 点的向心加速度的大小为 2 B a l  （2） 因为是匀角速转动，B 点的切向加速度为 0，故 Ba 也是 B 点的加速度，其方向沿 BA 方向．因为 C 点绕 D 轴作 圆周运动，其速度的大小用 C v 表示，方向垂直于杆 CD，在考察的时刻，由图可知，其方向沿杆 BC 方向．因 BC 是刚性杆，所以 B 点和 C 点沿 BC 方向的速度必相等，故有 C π 2 cos 4 2   l B v v （3） 此时杆 CD 绕 D 轴按顺时针方向转动，C 点的法向加速度 2 C Cn a CD  v （4） 由图可知CD l  2 2 ，由（3）、（4）式得 2 2 8 Cn a l   （5） 其方向沿 CD 方向． 下面来分析 C 点沿垂直于杆 CD 方向的加速度，即切向加速度 Ct a ．因 为 BC 是刚性杆，所以 C 点相对 B 点的运动只能是绕 B 的转动，C 点相对 B 点的速度方向必垂直于杆 BC．令 CB v 表示其速度的大小，根据速度合成公式有 CB C B      v v v 由几何关系得 2 2 2 2 2 2 CB B C B v v v v     l （6） 由于 C 点绕 B 作圆周运动，相对 B 的向心加速度 2 CB CB a CB  v （7） 因为CB l  2 ，故有 2 2 4 CB a l   （8） 其方向垂直杆 CD. 由（2）式及图可知，B 点的加速度沿 BC 杆的分量为   π cos 4 B B BC a a  （9） 所以 C 点相对 A 点（或 D 点）的加速度沿垂直于杆 CD 方向的分量   3 2 2 4 Ct CB B BC a a a l     （10） C 点的总加速度为 C 点绕 D 点作圆周运动的法向加速度 Cn a 与切向加速度 Ct a 的合加速度，即 CB  v A C D B B v  C  v aCn aC t aC  中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理