
1.Clausius不等式 设温度相同的两个高、低温热源间有一个可逆 热机和一个不可逆热机。 则:=马+=1+ -T=1- T 2 2 T T 根据Carnot)定理: 7<7R 则 g+<0 TT 推广为与个热源接触的任意不可逆过程,得:
1. Clausius 不等式 设温度相同的两个高、低温热源间有一个可逆 热机和一个不可逆热机。 T T T T T − = = − h c c R h h 1 根据Carnot定理: I R Q Q T T + c h c h 则 0 I 0 n i i i Q T < 推广为与n个热源接触的任意不可逆过程,得: h c c I h h 1 Q Q Q Q Q + 则: = = +
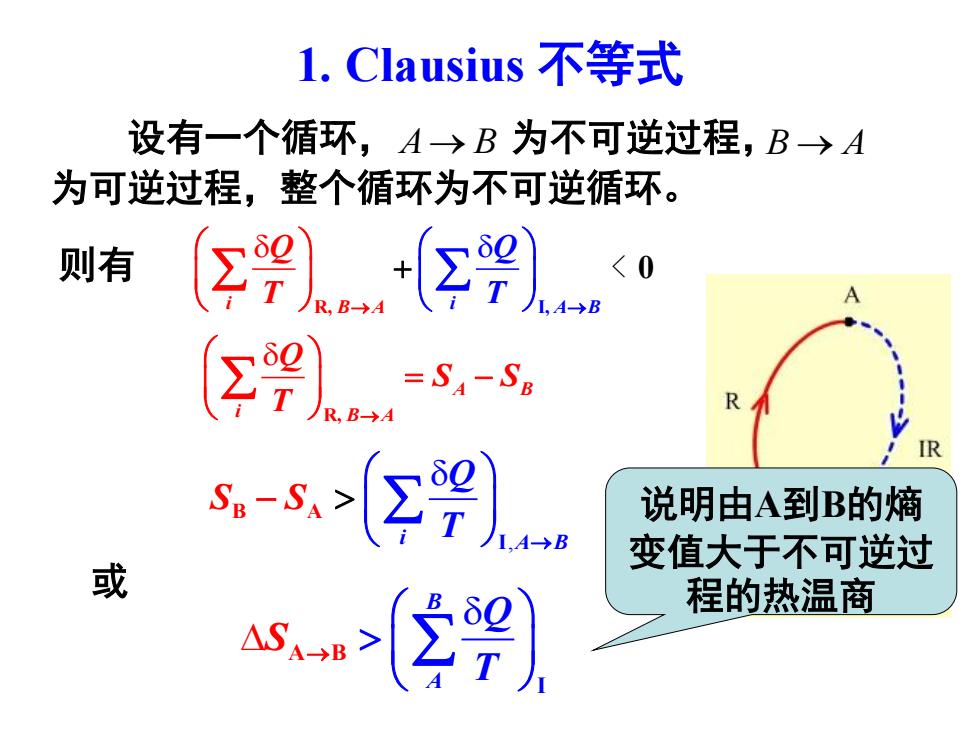
l.Clausius不等式 设有一个循环,A→B为不可逆过程,B→A 为可逆过程,整个循环为不可逆循环。 则有 <0 Σ9) =SA-Sp R s-s>Σ9) 说明由A到B的熵 变值大于不可逆过 或 as>2劉 程的热温商
1. Clausius 不等式 A B i B A Q S S T R, → = − B A S Q T A I →B 或 , i A B Q S T S I B A → − 设有一个循环, 为不可逆过程, 为可逆过程,整个循环为不可逆循环。 A B → B A → i B A i A B Q T Q T R, I, 0 → → + 则有 < 说明由A到B的熵 变值大于不可逆过 程的热温商
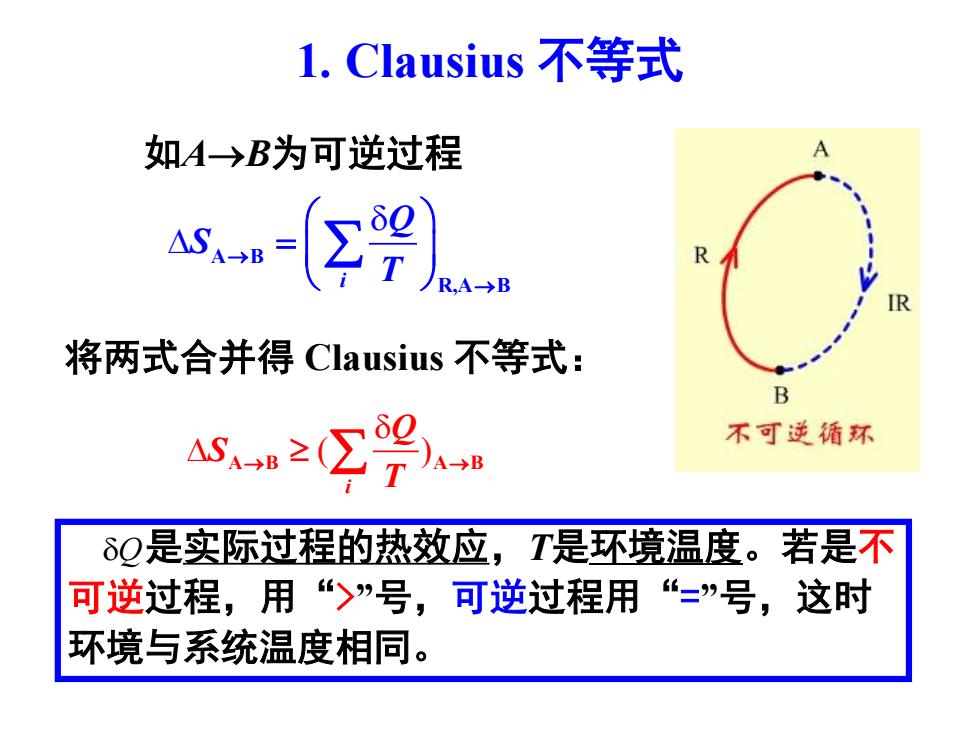
l.Clausius不等式 如A→B为可逆过程 s RA→B R 将两式合并得Clausius不等式: B ASB2(∑)8 不可逆循环 δQ是实际过程的热效应,T是环境温度。若是不 可逆过程,用“>”号,可逆过程用“=”号, 这时 环境与系统温度相同
1. Clausius 不等式 如A→B为可逆过程 A B i R,A B Q S T → → = ( ) A B A B i Q S T → → 将两式合并得 Clausius 不等式: 是实际过程的热效应,T是环境温度。若是不 可逆过程,用“>”号,可逆过程用“=”号,这时 环境与系统温度相同。 Q

l.Clausius不等式 对于微小变化: >不可逆过程 dS≥ δ2 T =可逆过程 这些都称为Clausius不等式,也可作为热力 学第二定律的数学表达式
1. Clausius 不等式 这些都称为 Clausius 不等式,也可作为热力 学第二定律的数学表达式。 Q S T d 对于微小变化: >不可逆过程 = 可逆过程

2.熵增加原理 对于绝热系统 δ0=0 所以Clausius不等式为 dS≥0 等号表示绝热可逆过程,不等号表示绝热不 可逆过程。 熵增加原理可表述为:在绝热条件下,趋向于平 衡的过程使系统的熵增加。 或者说在绝热条件下,不可能发生熵减少的过程 如果是一个隔离系统,环境与系统间既无热的 交换,又无功的交换,则熵增加原理可表述为: 一个隔离系统的熵永不减少
2. 熵增加原理 对于绝热系统 = Q 0 d 0 S 等号表示绝热可逆过程,不等号表示绝热不 可逆过程。 如果是一个隔离系统,环境与系统间既无热的 交换,又无功的交换,则熵增加原理可表述为: 所以Clausius 不等式为 熵增加原理可表述为:在绝热条件下,趋向于平 衡的过程使系统的熵增加。 或者说在绝热条件下,不可能发生熵减少的过程 一个隔离系统的熵永不减少